Two Dialogs on Searle
If a computer can beat you at chess,
it can beat you at philosophy.
The first dialog explores the fundamental mistake Searle makes in his "Chinese Room Argument", namely that while in the general case syntax is insufficient for semantics, programming languages are semantics with syntax. I have written about Searle before (the latest here), but that's me making a case to an empty courtroom. Here, I carry on an adversarial conversation with Grok 3.0 and let it judge the result.
The second dialog considers where Searle can maintain his conclusion that computers cannot be conscious without his "syntax is insufficient for semantics" pillar except by denying the Church-Turing Hypothesis, which he affirms. My position is that he can't, Grok tried to show he can.
Grok is overly verbose, yet sometimes exhibits what appears to be keen insight and sometimes says things in a way that make me jealous that it can be a better wordsmith than me. Grok doesn't get mad, doesn't get frustrated, and doesn't get tired (at least as long as I maintain my $30/month subscription). It is a far more challenging opponent than I typically have access to.
In the future, these discussions will be multi-way with humans and chatbots pushing the boundaries, with the machines keeping everyone honest - demanding definitions, uncovering tacit assumptions, noticing loops, and keeping score. We will be able to save a transcript then ask ChatGPT to read it and comment on it. New insights can be added, repetitious material ignored. The possibility of positive transform is exciting.
Dialog 1 - Searle's mistake
Dialog 2 - Searle and the Church-Turing Hypothesis
Bohr on Nature

What's interesting about this is that what Bohr thinks we can say about nature is also what we think we can say about consciousness. We recognize consciousness by behavior (cf. Searle's Chinese Room), but we cannot say whether consciousness is produced by that behavior or whether it is revealed by that behavior.
AGI
If AGI doesn't include insanity as well as intelligence then it may be artificial, but it won't be general.
In "Gödel, Escher, Bach" Hofstadter wrote:
It is an inherent property of intelligence that it can jump out of the task which it is performing, and survey what it is done; it is always looking for, and often finding, patterns.1
Over 400 pages later, he repeats this idea:
This drive to jump out of the system is a pervasive one, and lies behind all progress and art, music, and other human endeavors. It also lies behind such trivial undertakings as the making of radio and television commercials.2
For intelligence to be general, the ability to jump must be in all directions.
[1] Pg. 37
[2] Pg. 478
This idea is repeated in this post from almost 13 years ago. Have I stopped jumping outside the lines?
Quote
1,2
Whether or not the √2 is irrational cannot be shown by measuring it.
Whether or not the Church-Turing hypothesis is true cannot be shown by thinking about it.
[1] "Euclidean and Non-Euclidean Geometries", Greenberg, Marvin J., Second Edition, pg. 7: "The point is that this irrationality of length could never have been discovered by physical measurements, which always include a small experimental margin of error."
[2] This quote is partially inspired by Scott Aaronson's "PHYS771 Lecture 9: Quantum" where he talks about the necessity of experiments.
Searle's Chinese Room: Another Nail
[updated 3/9/2024 - note on Searle's statement that "programs are not machines"]
[updated 10/8/2024;02/09/2025] - added "Searle's Fundamental Error" at beginning to present the gist of why his argument is wrong]
Searle's Fundamental Error
Searle's claim is that because syntax is insufficient for semantics that computers cannot understand meaning the way humans can. What Searle misses is that computer languages are semantics that happen to have syntax. Every computer language is equivalent to a network of logic gates and logic gates specify behavior. These networks can easily implement semantics.Introduction
I have discussed Searle's "Chinese Room Argument" twice before: here and here. It isn't necessary to review them. While both of them argue against Searle's conclusion, they aren't as complete as I think they could be. This is one more attempt to put another nail in the coffin, but the appeal of Searle's argument is so strong - even though it is manifestly wrong - that it may refuse to stay buried. The Addendum explains why.Searle's paper, "Mind, Brains, and Programs" is here. He argues that computers will never be able to understand language the way humans do for these reasons:
- Computers manipulate symbols.
- Symbol manipulation is insufficient for understanding the meaning behind the symbols being manipulated.
- Humans cannot communicate semantics via programming.
- Therefore, computers cannot understand symbols the way humans understand symbols.
- Is certainly true. But Searle's argument ultimately fails because he only considers a subset of the kinds of symbol manipulation a computer (and a human brain) can do.
- Is partially true. This idea is also expressed as "syntax is insufficient for semantics." I remember, from over 50 years ago, when I started taking German in 10th grade. We quickly learned to say "good morning, how are you?" and to respond with "I'm fine. And you?" One morning, our teacher was standing outside the classroom door and asked each student as they entered, the German equivalent of "Good morning," followed by the student's name, "how are you?" Instead of answering from the dialog we had learned, I decided to ad lib, "Ice bin heiss." My teacher turned bright red from the neck up. Bless her heart, she took me aside and said, "No, Wilhem. What you should have said was, 'Es ist mir heiss'. To me it is hot. What you said was that you are experiencing increased libido." I had used a simple symbol substitution, "Ich" for "I", "bin" for "am", and "heiss" for "hot", temperature-wise. But, clearly, I didn't understand what I was saying. Right syntax, wrong semantics. Nevertheless, I do now understand the difference. What Searle fails to establish is how meaningless symbols acquire meaning. So he handicaps the computer. The human has meaning and substitution rules; Searle only allows the computer substitution rules.
- Is completely false.
To understand why 2 is only partially true, we have to understand why 3 is false.
- A Turing-complete machine can simulate any other Turing machine. Two machines are Turing equivalent if each machine can simulate the other.
- The lambda calculus is Turing complete.
- A machine composed of NAND gates (a "computer" in the everyday sense) can be Turing complete.
- A NAND gate (along with a NOR gate) is a "universal" logic gate.
- Memory can also be constructed from NAND gates.
- The equivalence of a NAND-based machine and the lambda calculus is demonstrated by instantiating the lambda calculus on a computer.1
- From 3, every computer program can be written as expressions in the lambda calculus; every computer program can be expressed as an arrangement of logic gates. We could, if we so desired, build a custom physical device for every computer program. But it is massively economically unfeasible to do so.
- Because every computer program has an equivalent arrangement of NAND gates2, a Turing-complete machine can simulate that program.
- NAND gates are building-blocks of behavior. So the syntax of every computer program represents behavior.
- Having established that computer programs communicate behavior, we can easily see what Searle's #2 is only partially true. Symbol substitution is one form of behavior. Semantics is another. Semantics is "this is that" behavior. This is the basic idea behind a dictionary. The brain associates visual, aural, temporal, and other sensory input and this is how we acquire meaning [see "The Problem of Qualia"]. Associating the visual input of a "dog", the sound "dog", the printed word "dog", the feel of a dog's fur, are how we learn what "dog" means. We have massive amounts of data that our brain associates to build meaning. We handicap our machines, first, by not typically giving them the ability to have the same experiences we do. We handicap them, second, by not giving them the vast range of associations that we have. Nevertheless, there are machines that demonstrate that they understand colors, shapes, locations, and words. When told to describe a scene, they can. When requested to "take the red block on the table and place it in the blue bowl on the floor", they can.
I was able to correct my behavior by establishing new associations: temperature and libido with German usage of "heiss". That associative behavior can be communicated to a machine. A machine, sensing a rise in temperature, could then inform an operator of its distress, "Es ist mir heiss!". Likely (at least, for now) lacking libido, it would not say, "Ich bin heiss."
Having shown that Searle's argument is based on a complete misunderstanding of computation, I wish to address selected statements in his paper.
Read More...
The Physical Ground of Logic
[updated 14 January 2024 to add note on semantics and syntax]
[updated 17 January 2024 to add note on universality of NAND and NOR gates]
[updated 26 March 2024 to add note about philosophical considerations of rotation]
The nature of logic is a contested philosophical question. One position is that logic exists independently of the physical realm; another is that it is a fundamental aspect of the physical realm; another is that it is a product of the physical realm. These correspond roughly to the positions of idealism, dualism, and materialism.
Here, the physical basis for logic is demonstrated. This doesn't disprove idealism, dualism, or materialism; but it does make it harder to find a bright line of demarcation between them and a way to make a final determination as to which might correspond to reality.
There are multiple logics. As "zeroth-order" (or "propositional logic") is the basis of all higher logics, we start here.
Begin with two arbitrary distinguishable objects. They can be anything: coins with heads and tails; bees and bears; letters in an alphabet, silicon and carbon atoms. Two unique objects, "lefty" and "righty" are chosen. The main reason is to use objects for which there is no common associated meaning. Meaning must not creep in "the back door" and using unfamiliar objects should help that from inadvertently happening. A secondary engineering reason, with a strong philosophical connection, will be demonstrated later.
| Lefty | Righty |
|---|---|
| \ | | |
These two objects can be combined four ways as shown in the next table. You should be able to convince yourself that these are the only four ways for these combinations to occur. For convenience, each input row and column is labeled for future reference.
| $1 | $2 | |
|---|---|---|
| C0 | \ | \ |
| C1 | \ | | |
| C2 | | | \ |
| C3 | | | | |
Next, observe that there are sixteen ways to select an object from each of the four combinations. You should be able to convince yourself that these are the only ways for these selections to occur. For convenience, the selection columns are labelled for future reference. The selection columns correspond to the combination rows.
| S0 | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | S10 | S11 | S12 | S13 | S14 | S15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C0 | | | | | | | | | | | | | | | | | \ | \ | \ | \ | \ | \ | \ | \ |
| C1 | | | | | | | | | \ | \ | \ | \ | | | | | | | | | \ | \ | \ | \ |
| C2 | | | | | \ | \ | | | | | \ | \ | | | | | \ | \ | | | | | \ | \ |
| C3 | | | \ | | | \ | | | \ | | | \ | | | \ | | | \ | | | \ | | | \ |
Now the task is to build physical devices that combine these two inputs and select an output according to each selection rule. Notice that in twelve of the selection rules it is possible to get an output that was not an input. On the one hand, this is like pulling a rabbit out of a hat. It looks like something is coming out that wasn't going in. On the other hand, it's possible to build a device with a "hidden reservoir" of objects so that the required object is produced. But this is the engineering reason why "lefty" and "righty" are the way they are. "lefty" can be turned into "righty" and "righty" can be turned into "lefty" by rotating the object and rotation is a physical operation on a physical object.
This engineering decision has interesting implications. It ensures that logic is self-contained: what goes in is what comes out. If it doesn't go in, it doesn't come out. The logic gate "not" turns truth into falsity and falsity into truth by a simple rotation. Philosophically, this means that truth and falsity are stance dependent; truth depends on how you look at it. Moving an observer is equivalent to rotating the symbol.
Suppose we can build a device which has the behavior of S7:
We know how to build devices which have the behavior of S7, which is known as a "NAND" (Not AND)1 gate. There are numerous ways to build these devices: with semiconductors that use electricity, with waveguides that use fluids such as air and water, with materials that can flex, neurons in the brain, even marbles.2 NAND gates and NOR gates (S1) are known as universal gates, since arrangements of each gate can produce all of the other selection operations. The demonstration with NAND gates is here. The correspondence between digital logic circuits and propositional logic has been known for a long time.
John Harrison writes3:Digital design Propositional Logic logic gate propositional connective circuit formula input wire atom internal wire subexpression voltage level truth value
The interesting bit now is how to get "truth values" into, or out of, the system. Typically, we put "truth" into the system. We look at the pattern for S7, say, and note that if we arbitrarily declare that "lefty" is "true", then "righty" is false, then we get the logical behavior that is familiar to us. Because digital computers work with low and high voltages, it is more common to arbitrarily make one of them 0 and the other 1 and then to, again arbitrarily, make the convention that one of them (typically 0) represents false and the other (either 1 or non-zero) true.
This way of looking at the system leads to the idea that truth is an emergent behavior in complex systems. Truth is found in the arrangement of the components, not in the components themselves.
But this isn't the only way of looking at the system.
Let us break down the what the internal behavior of each selection process has to accomplish. This behavior will be grouped in order of increasing complexity. To do this, we have to introduce some notation.
~ is the "rotate" operation. ~\ is |; ~| is \.
= tests for equality, e.g. $1 = $2 compares the first input value with the second input value.
? equal-path : unequal-path takes action based on the result of the equal operator.
\ = \ ? | : \ results in |, since \ is equal to \.
\ = | ? | : \ results in \, since \ is not equal to |.
| Selection | Behavior |
|---|---|
| S0 | | |
| S15 | \ |
The second group outputs one of the inputs, perhaps with rotation:
| Selection | Behavior |
|---|---|
| S12 | $1 |
| S3 | ~$1 |
| S10 | $2 |
| S5 | ~$2 |
The third group compares the inputs for equality and produces an output for the equal path and another for the unequal path:
| Selection | Behavior |
|---|---|
| S8 | $1 = $2 ? $1 : | |
| S14 | $1 = $2 ? $1 : \ |
| S1 | $1 = $2 ? ~$1 : | |
| S7 | $1 = $2 ? ~$1 : \ |
| S4 | $1 = $2 ? | : $1 |
| S2 | $1 = $2 ? | : $2 |
| S13 | $1 = $2 ? \ : $1 |
| S11 | $1 = $2 ? \ : $2 |
| S6 | $1 = $2 ? | : \ |
| S9 | $1 = $2 ? \ : | |
It's important to note that whatever the physical layer is doing, if the device performs according to these combination and selection operations then the internal layer is doing these logical operations.
The next step is to figure out how to do the equality operation. We might think to use S9 but this doesn't help. It still requires the arbitrary assignment of "true" to one of the input symbols. The insight comes if we consider the input symbol as an object that already has the desired behavior. Electric charge implements the equality behavior: equal charges repel; unequal charges attract. If the input objects repel then we take the "equal path" and output the required result; if they attract we take the "unequal path" and output that answer.
In this view, "truth" and "falsity" are the behaviors that recognize themselves and disregard "not themselves." And we find that nature provides this behavior of self-identification at a fundamental level. Charge - and its behavior - is not an emergent property in quantum mechanics.
What's interesting is that nature gives us two ways of looking at it and discovering two ways of explaining what we see without, apparently, giving us a clue as to which is the "right" way to look at it. Looking one way, truth is emergent. Looking way, truth is fundamental. Philosophers might not like this view of truth (that truth is the behavior of self-recognition), but our brains can't develop any other notions of truth apart from this "computational truth."
Hiddenness
How the fact that the behavior of electric charge is symmetric, as well as the physical/logical layer distinction, plays into subjective first person experience is here.Syntax and Semantics
In natural languages, it is understood that the syntax of a sentence is not sufficient to understand the semantics of the sentence. We can parse "'Twas brillig, and the slithy toves" but, without additional information, cannot discern its meaning. It is common to try to extend this principle to computation to assert that the syntax of computer languages cannot communicate meaning to a machine. But logic gates have syntax and behavior. The syntax of S7 can take many forms: S7, (NAND x y), NOT AND(a, b); even the diagram of S7, above. The behavior associated with the syntax is: $1 = $2 ? ~$1 : \. So the syntax of a computer language communicates behavior to the machine. As will be shown later, meaning is the behavior of association, this is that. So computer syntax communicates behavior, which can include meaning, to the machine.
More elaboration on how philosophy misunderstands computation is here.
Notes
An earlier derivation of this same result using the Lambda Calculus is here. But this demonstration, while inspired by the Lambda Calculus, doesn't require the heavier framework of the calculus.[1] An "AND" gate has the behavior of S8.
[2] There is a theory in philosophy known as "multiple realizibility" which argues that the ability to implement "mental properties" in multiple ways means that "mental properties" cannot be reduced to physical states. As this post demonstrates, this is clearly false.
[3] "A Survey of Automated Theorem Proving", pg. 27.
Dialog with an Atheist #3
I prefer the academic definition of atheist: Belief that there are no gods.
I do not identify as an atheist.
I am a militant agnostic. I don't know, and you don't either.
@theosib2 and I have had numerous discussions about computer science and religion. In particular, we have gone back and forth about how we can test for 3rd party consciousness. It is absolutely impossible to objectively determine if something is conscious. The Inner Mind shows the physical reason why this is true. However, @theosib2 maintains this is not the case, even though I have pressed him to state what a function with this behavior is doing:
ξξ→ζ ξζ→ξ ζξ→ξ ζζ→ξ
Objectively, it's a lookup table. Objectively, it has no meaning and no purpose. It's just a swirl of meaningless objects. Subjectively, it does have meaning and purpose, but we can't decide what it is. It could be a NAND gate or a NOR gate. Arrange these gates into a computer program and we might be able to determine what it is doing by its overall behavior. But we have to be able to map its behavior into behavior that we recognize within ourselves.
With this as background, I responded to @theosib2:
“I’m conscious!”
“I don’t think so. You’re not carbon based.”
“I passed your Turing test, multiple times, when you couldn’t asses my form. I’m conscious, dammit.”
“I don’t know that you are. And you don’t, either.”
@theosib2 responded identically to "Victorian dad":
If only we could have a rigorous definition of consciousness. Then your comparison might be valid.
The endgame then played out as before:
Are you conscious?
Sometimes I wonder (with link to They Might Be Giants "Am I Awake?")
But only sometimes, right?
The atheist either has a problem with either knowing things that are subjectively known, or admitting the validity of subjective knowledge. Because if subjective knowledge is validly known, then demands for objective evidence for God are groundless. Because we have objective knowledge that mind is only known subjectively.
Farpoint Engineering
- FASTPOINT-80 product sheet
- Microway advertisement (the Micro Channel boards under Math Coprocessors).
- From BYTE magazine, August, 1990.
- Fractal demo code (386 assembly)
I wrote a terminate-and-stay-resident program to install an "int 15h" interface between applications and the hardware, but that code is long lost.
Eric Schmidt
PERFCT (BASIC)
MLTPUN (FORTRAN)
SPAGE (FORTRAN)
[1] I really wish I still had FRESEQ, which I wrote in FORTRAN, that resequenced FORTRAN line and statement numbers like the built-in resequence command did for BASIC programs. Sometime around then I also wrote an INTEL 4004/4040/8008/8080 macro assembler in FORTRAN, but I don't have that, either.
The Inner Mind
[Similar introductory presentation here]
Philosophy of mind has the problem of "mental privacy" or "the problem of first-person perspective." It's a problem because philosophers can't account for how the first person view of consciousness might be possible. The answer has been known for the last 100 years or so and has a very simple physical explanation. We know how to build a system that has a private first person experience.
Let us use two distinguishable physical objects:

These shapes of these objects are arbitrary and were chosen so as not to represent something that might have meaning due to familiarity. While they have rotational symmetry, this is for convenience for something that is not related to the problem of mental privacy.
Next, let us build a physical device that takes two of these objects as input and selects one for output. Parenthesis will be used to group the inputs and an arrow will terminate with the selected output. The device will operate according to these four rules:

A network of these devices can be built such that the output of one device can be used as input to another device.
It is physically impossible to tell whether this device is acting as a NAND gate or as a NOR gate. We are taught that a NAND gate maps (T T)→F, (T F)→T, (F T)→T, and (F F)→T; (1 1)→0, (1 0)→1, (0 1)→1, (0 0)→0 and that a NOR gate maps (T T)→F, (T F)→F, (F T)→F, (F F)→T; (1 1)→0, (1 0)→0, (0 1)→0, (0 0)→1. But these traditional mappings obscure the fact that the symbols are arbitrary. The only thing that matters is the behavior of the symbols in a device and the network constructed from the devices. Because you cannot tell via external inspection what the device is doing you cannot tell via external inspection what the network of devices is doing. All an external observer sees is the passage of arbitrary objects through a network.1
To further complicate the situation, computation uses the symbol/value distinction: this symbol has that value. But "value" is just elements of the alphabet and so are identical to symbols when viewed externally. That means that to fully understand what a network is doing, you have to discern whether a symbol is being used as a symbol or as a value. But this requires inner knowledge of what the network is doing, which leads to infinite regress. You have to know what the network is doing on the inside to understand what the network is doing from the outside.
Or the network has to tell you what it's doing. NAND and NOR gates are universal logic gates which can be used to construct a "universal" computing device.2
So we can construct a device which can respond to the question "what logic gate was used in your construction?"
Depending on how it was constructed, its response might be:
- "I am made of NAND gates."
- "I am made of NOR gates."
- "I am made of NAND and NOR gates. My designer wasn't consistent throughout."
- "I don't know."
- "What's a logic gate?"
- "For the answer, deposit 500 bitcoin in my wallet."
Before the output device is connected to the system so that the answer can be communicated, there is no way for an external observer to know what the answer will be.
All an external observer has to go on is what the device communicates to that observer, whether by speech or some other behavior.3
And even when the output device is active and the observer receives the message, the observer cannot tell whether the answer given corresponds to how the system was actually constructed.
So extrospection cannot reveal what is happening "inside" the circuit. But note that introspection cannot reveal what is happening "outside" the circuit. The observer doesn't know what the circuit is doing; the subject doesn't know how it was built. It may think it does, but it has no way to tell.
[1] Technology has advanced to the point where brain signals can be interpreted by machine, e.g. here. But this is because these machines are trained by matching a person's speech to the corresponding brain signals. Without this training step, the device wouldn't work. Because our brains are similar, it's likely possible that a speaking person could train such a machine for a non-vocal person.
[2] I put universal in quotes because a universal Turing machine requires infinite memory and this would require an infinite number of gates. Our brains don't have an infinite number of neurons.
[3] See also Quss, Redux, since this has direct bearing on yet another problem that confounds philosophers, but not engineers.
Venn Diagrams
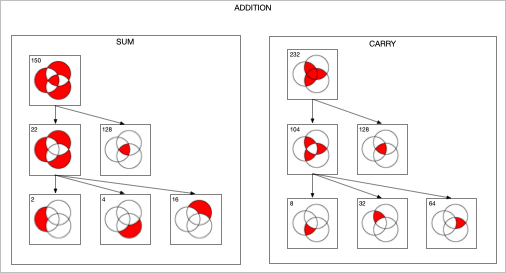
Twelve years ago I played around with designing digital circuits (1, 2, 3) and wrote some code to help in that endeavor. If you can evaluate logical expressions you ought to be able to visualize those expressions. So I extended this code to generate a Venn diagram of an expression. The sum and carry portions of an adder are striking. Click for larger images.
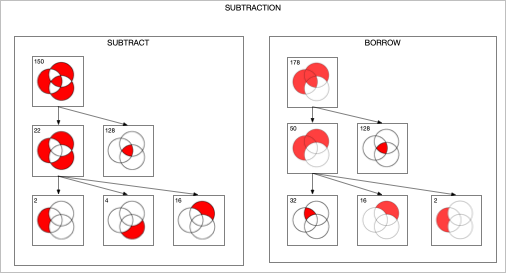
The Venn diagram for the subtraction and borrow equations of a subtraction circuit are similar:
I then produced an animated GIF of all of the 256 Venn diagrams for an equation of 3 variables. The right side is the complement of the equation on the left. 128 images were created, then I used Flying Meat's Retrobatch to resize each image, add the image number, and convert to .GIF format. Then I used the open source gifsicle to produce the final animated .GIF.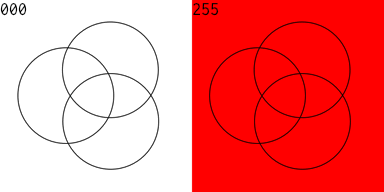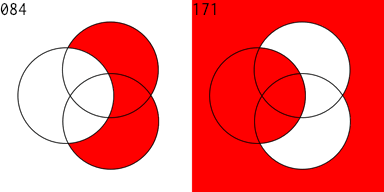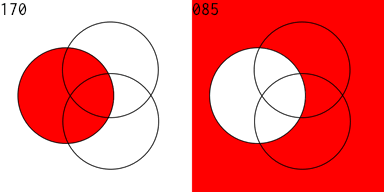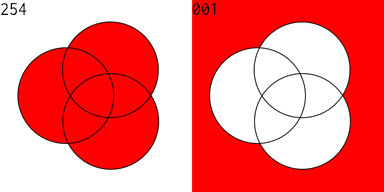
Solid State Jabberwocky
'Twas Burroughs, and the ILLIACS
Did JOSS and SYSGEN in the stack;
All ANSI were the acronyms,
and the Eckert-Mauchly ENIAC.
"Beware the deadly OS, son!
The Megabyte, the JCL!
Beware the Gigabit, and shun
The ponderous CODASYL!"
He took his KSR in hand:
Long time the Armonk foe he sought.
So rested he by the Syntax Tree
And APL'd in thought.
And as in on-line thought he stood,
the CODASYL of verbose fame,
Came parsing through the Chomsky wood,
And COBOL'ed as it came!
One, two! One, two! And through and through
The final pol at last drew NAK!
He left it dead, and with its head
He iterated back.
And hast thou downed old Ma Bell?
Come to my arms, my real-time boy!
Oh, Hollerith day! Array! Array!
He macroed in his joy.
'Twas Burroughs, and the ILLIACS
Did JOSS and SYSGEN in the stack;
All ANSI were the acronyms,
and the Eckert-Mauchly ENIAC.
-- William J. Wilson
The only reference to this on the web that I can find is at archive.org. This poem is 50 years old. I wonder who else, besides me, remembers it?
Quus, Redux
Philip Goff explores Kripke's quss function, defined as:
In English, if the two inputs are both less than 100, the inputs are added, otherwise the result is 5.
(defparameter N 100)
(defun quss (a b)
(if (and (< a N) (< b N))
(+ a b)
5))
Goff then claims:
Rather, it’s indeterminate whether it’s adding orquadding.
This statement rests on some unstated assumptions. The calculator is a finite state machine. For simplicity, suppose the calculator has 10 digits, a function key (labelled "?" for mystery function) and "=" for result. There is a three character screen, so that any three digit numbers can be "quadded". The calculator can then produce 1000x1000 different results. A larger finite state machine can query the calculator for all one million possible inputs then collect and analyze the results. Given the definition of quss, the analyzer can then feed all one million possible inputs to quss, and show that the output of quss matches the output of the calculator.
Goff then tries to extend this result by making N larger than what the calculator can "handle". But this attempt fails, because if the calculator cannot handle bigN, then the conditionals (< a bigN) and (< b bigN) cannot be expressed, so the calculator can't implement quss on bigN. Since the function cannot even be implemented with bigN, it's pointless to ask what it's doing. Questions can only be asked about what the actual implementation is doing; not what an imagined unimplementable implementation is doing.
Goff then tries to apply this to brains and this is where the sleight of hand occurs. The supposed dichotomy between brains and calculators is that brains can know they are adding or quadding with numbers that are too big for the brain to handle. Therefore, brains are not calculators.
The sleight of hand is that our brains can work with the descriptions of the behavior, while most calculators are built with only the behavior. With calculators, and much software, the descriptions are stripped away so that only the behavior remains. But there exists software that works with descriptions to generate behavior. This technique is known as "symbolic computation". Programs such as Maxima, Mathematica, and Maple can know that they are adding or quadding because they can work from the symbolic description of the behavior. Like humans, they deal with short descriptions of large things1. We can't write out all of the digits in the number 10^120. But because we can manipulate short descriptions of big things, we can answer what quss would do if bigN were 10^80. 10^80 is less than 10^120, so quss would return 5. Symbolic computation would give the same answer. But if we tried to do that with the actual numbers, we couldn't. When the thing described doesn't fit, it can't be worked on. Or, if the attempt is made, the old programming adage, Garbage In - Garbage Out, applies to humans and machines alike.
[1] We deal with infinity via short descriptions, e.g. "10 goto 10". We don't actually try to evaluate this, because we know we would get stuck if we did. We tag it "don't evaluate". If we actually need a result with these kinds of objects, we get rid of the infinity by various finite techniques.
[2] This post title refers to a prior brief mention of quss here. In that post, it suggested looking at the wiring of a device to determine what it does. In this post, we look at the behavior of the device across all of its inputs to determine what it does. But we only do that because we don't embed a rich description of each behavior in most devices. If we did, we could simply ask the device what it is doing. Then, just as with people, we'd have to correlate their behavior with their description of their behavior to see if they are acting as advertised.
Truth, Redux
Logic is mechanical operations on distinct objects. At it simplest, logic is the selection of one object from a set of two (see "The road to logic", or "Boolean Logic"). Consider the logic operation "equivalence". If the two input objects are the same, the output is the first symbol in the 0th row ("lefty"). If the two input objects are different, the output is the first symbol in the 3rd row ("righty").
If this were a class in logic, the meaningless symbols "lefty" and "righty" would be replaced by "true" and "false".
But we can't do this. Yet. We have to show how to go from the meaningless symbols "lefty" and "righty" to the meaningful symbols "T" and "F". The lambda calculus shows us how. The lambda calculus describes a universal computing device using an alphabet of meaningless symbols and a set of symbols that describe behaviors. And this is just what we need, because we live in a universe where atoms do things. "T" and "F" need to be symbols that stand for behaviors.
We look at these symbols, we recognize that they are distinct, and we see how to combine them in ways that make sense to our intuitions. But we don't know we do it. And that's because we're "outside" these systems of symbols looking in.
Put yourself inside the system and ask, "what behaviors are needed to produce these results?" For this particular logic operation, the behavior is "if the other symbol is me, output T, otherwise output F". So you need a behavior where a symbol can positively recognize itself and negatively recognize the other symbol. Note that the behavior of T is symmetric with F. "T positively recognizes T and negatively recognizes F. F positively recognizes F and negatively recognizes T." You could swap T and F in the output column if desired. But once this arbitrary choice is made, it fixes the behavior of the other 15 logic combinations.
In addition, the lambda calculus defines true and false as behaviors.1 It just does it at a higher level of abstraction which obscures the lower level.
In any case, nature gives us this behavior of recognition with electric charge. And with this ability to distinguish between two distinct things, we can construct systems that can reason.
[1] Electric Charge, Truth, and Self-Awareness. This was an earlier attempt to say what this post says. YMMV.
The Universe Inside
Let us replace distinguishable objects with objects that distinguish themselves:
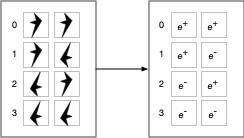
Then the physical operation that determines if two elements are equal is:

As shown in the previous post, e+ (the positron and its behavior) and e- (the electron and its behavior) are the behaviors assigned to the labels "true" and "false". One could swap e+ and e-. The physical system would still exhibit consistent logical behavior. In any case, this physical operation answers the question "are we the same?", "Is this me?", because these fundamental particles are self-identifying.
From this we see that logical behavior - the selection of one item from a set of two - is fully determined behavior.
In contrast to logic, nature features fully undetermined behavior where a selection is made from a group at random. The double-slit experiment shows the random behavior of light as it travels through a barrier with two slits and lands somewhere on a detector.
In between these two options, there is partially determined, or goal directed behavior where selections are made from a set of choices that lead to a desired state. It is a mixture of determined and undetermined behavior. This is where the problem of teleology comes in. To us, moving toward a goal state indicates purpose. But what if the goal is chosen at random? Another complication is that, while random events are unpredictable, sequences of random events have predictable behavior. Over time, a sequence of random events with tend to its expected value. We are faced with having to decide if randomness indicates no purpose or hidden purpose, agency or no agency.
In this post, from 2012, I made a claim about a relationship between software and hardware. In the post, "On the Undecidability of Materialism vs. Idealism", I presented an argument using the Lambda Calculus to show how software and hardware are so entwined that you can't physically take them apart. This low-level view of nature reinforces these ideas. All logical operations are physical (all software is hardware). Not all physical operations are logical (not all hardware is software). Computing is behavior and the behavior of the elementary particles cannot be separated from the particles themselves. If we're going to choose between idealism and physicalism, it must be based on a coin flip2.
If computers are built of logic "circuits" then computer behavior ought to be fully determined. But when we add peripherals to the system and inject random behavior (either in the program itself, or from external sources), we get non-logical behavior in addition to logic. If a computer is a microcosm of the brain, the brain is a microcosm of the universe.
[1] Quarks have fractional charge, but quarks aren't found outside the atomic nucleus. The strong nuclear force keeps them together. Electrons and positrons are elementary particles.
[2] Dualism might be the only remaining choice, but I think that dualism can't be right. That's a post for another day.
Searle's Chinese Room Argument
[Work in progress... revisions to come]
Searle's "Minds, Brains, and Programs" is an attempt to show that computers cannot think the way humans do and so any effort to create human-level artificial intelligence is doomed to failure. Searle's argument is clearly wrong. What I found most interesting in reading his paper is that Searle's understanding of computers and programs can be shown to be wrong without considering the main part of the argument at all! Of course, it's possible that his main argument is right but that his subsequent commentary is in error but the main mistakes in both will be demonstrated. Then several basic, but dangerous, ideas in his paper will be exposed.
On page 11, Searle presents a dialog where he answers the following five questions (numbers added for convenience for later reference):
1) "Could a machine think?"
The answer is, obviously, yes. We are precisely such machines.
2) "Yes, but could an artifact, a man-made machine think?"
Assuming it is possible to produce artificially a machine with a nervous system, neurons with axons and dendrites, and all the rest of it, sufficiently like ours, again the answer to the question seems to be obviously, yes. If you can exactly duplicate the causes, you could duplicate the effects. And indeed it might be possible to produce consciousness, intentionality, and all the rest of it using some other sorts of chemical principles than those that human beings use. It is, as I said, an empirical question.
3) "OK, but could a digital computer think?"
If by "digital computer" we mean anything at all that has a level of description where it can correctly be described as the instantiation of a computer program, then again the answer is, of course, yes, since we are the instantiations of any number of computer programs, and we can think.
4) "But could something think, understand, and so on solely in virtue of being a computer with the right sort of program? Could instantiating a program, the right program of course, by itself be a sufficient condition of understanding?"
This I think is the right question to ask, though it is usually confused with one or more of the earlier questions, and the answer to it is no.
5) "Why not?"
Because the formal symbol manipulations by themselves don't have any intentionality; they are quite meaningless; they aren't even symbol manipulations, since the symbols don't symbolize anything. In the linguistic jargon, they have only a syntax but no semantics. Such intentionality as computers appear to have is solely in the minds of those who program them and those who use them, those who send in the input and those who interpret the output.
With 1), by saying that we are thinking machines, we introduce the "Church-Turing thesis" which states that if a calculation can be done using pencil and paper by a human, that it can also be done by a Turing machine. If Searle concludes that humans can do something that computers cannot, in theory, do, then he will have deny the C-T thesis and show that what brains do is fundamentally different from what machines do. That brains are different in kind and not in degree.
With 2), Searle runs afoul of computability theory, as brilliantly expressed by Fenynman (Simulating Physics with Computers):
Computer theory has been developed to a point where it realizes that it doesn't make any difference; when you get to a universal computer, it doesn't matter how it's manufactured, how it's actually made.
So 2) doesn't help his argument and, by extension, nor does 3). It doesn't matter if the computer is digital or not (but, see here).
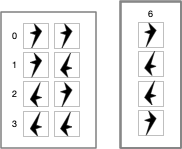
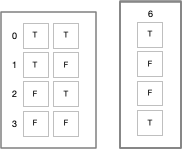
4) is based on a misunderstanding between "computer" and "program". We are so used to creating and running different programs on one piece of hardware that we think that there is some kind of difference between the two. But it's all hardware. Instead of the link to an article I wrote, let me demonstrate this. One of the fundamental aspects of computing is combination and selection. Binary logic is the mechanical selection of one object from two inputs. Consider this way, out of sixteen possible ways, to select one item. Note that it doesn't matter what the objects being selected are. Here we use "x" and "o", but the objects could be bears and bumblebees, or high and low pressure streams of electrons or water.
Table 1 object 1 object 2 result x x o x o x o x x o o x
Clearly, you can't get something from nothing, so the two cases where an object is given as a result when it isn't part of the input requires a bit of engineering. Nevertheless, these devices can be built.
Along with combination and selection another aspect of computation is composition. Let's convert the above table to a device that implements the selection given two inputs in a form that can be composed again and again.
We can arrange these devices so that, regardless of which of the two inputs are given (represented by "✽"), the output is always "x":
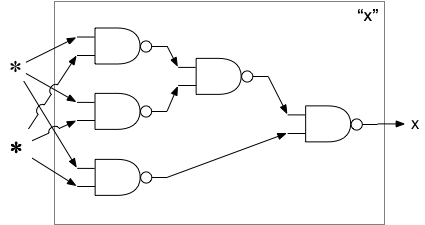
We can also make an arrangement so that the output is always "o", regardless of which inputs are used:

We now have all of the "important"1 aspects of a computer. If we replace "x" with 1 and "o" with 0 then we have all of the computational aspects of a binary computer. Every program is an arrangement of combination and selection operations. If it were economically feasible, we could build a unique network for every program. But the complexity would be overwhelming. One complicating factor is that the above does not support writeable memory. To go from a 0 to a 1 requires another node in the network, plus all of the machine states that can get to that node. For the fun of it, we show how the same logic device that combines two objects according to Table 1 can be wired together to provide memory:
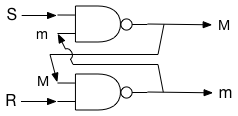
By design, S and R are initially "x", which means M and m are undefined. A continuous stream of "x" is fed into S and R.
Suppose S is set to "o" before resuming the stream of "x". Then:
S = o, M = x, R = x, m = o, S = x, M = x. This shows that when S is set to "o", M becomes "x" and stays "x".
Suppose R is set to "o" before resuming the stream of "x". Then:
R = o, m = x, S = x, M = o, R = x, m = x. This shows that when R is set to "x", M becomes "o" and stays "o", until S is reset to "o".
This shows that every program is a specification of the composition of combination and selection elements. The difference between a "computer" and a "program" is that programs are static forms of the computer: the arrangement of the elements are specified, but the symbols aren't flowing through the network.2 This means that if 1) and 2) are true, then the wiring of the brain is a program, just like each program is a logic network.
Finally, we deal with objection 5). Searle is wrong that there is no "intentionality" in the system. The "intentionality" is the way the symbols flow through the network and how they eventually interact with the external environment. Searle is right that the symbols are meaningless. So how do we get meaning from meaningless? For this, we turn to the Lambda Calculus (also here, and here: part 1, part 2). Meaning is simply a "this is that" relation. The Lambda Calculus shows how data can be associated with symbols. Our brains take in data from our eyes and associate it with a symbol. Our brains take in data from our ears and associate it with another symbol. If what we see is coincident with what we hear, we can add a further association between the "sight" symbol and the "hearing" symbol.3
The problem, then, is not with meaning, but with the ability to distinguish between symbols. The Lambda Calculus assumes this ability. We get meaning out of meaningless symbols because we can distinguish between symbols. Being able to distinguish between things is built into Nature: positive and negative charge is one example.
So Searle's dialog fails, unless you deny the first point and hold that we are not thinking machines. That is, we are something else that thinks. But this denies what we know about brain physiology.
But suppose that Searle disavows his dialog and asks that his thesis be judged solely on his main argument.
Addendum - 01/24/2025
The next update didn't occur until 05/04/20, which is less of an analysis of Searle's paper, but on what another philosopher wrote about Searle's paper. Here, I claimed that meaning is a this is that relation. In my latest take on Searle, a philosopher on X (nee Twitter) took issue with that. The objections that philosophers come up with are bizarre, to say the least. They can go to great lengths to hide that what they are really claiming, namely, that the brain is not Turing compatible. The problem with this is that it is a statement which can neither be proved - nor disproved - by thinking about it. It can only be asserted.[1] This is not meant to make light of all of the remaining hard parts of building a computer. But those details are to support the process of computation: combination, selection, and composition.
[2] One could argue that the steps for evaluating Lambda expressions (substitution, alpha reduction, beta reduction) are the "computer" and that the expressions to be evaluated are the "program". But the steps for evaluating Lambda expressions can be expressed as Lambda expressions. John McCarthy essentially did this with the development of the LISP programming language (here particularly section 4, also here). Given the equivalence of the Lambda Calculus, Turing machines, and implementations of Turing machines using binary logic, the main point stands.
[3] This is why there is no problem with "qualia".
Goto considered harmful
(defun read-input (&optional (result nil))
(let ((value (read)))
(if (equalp value 99999)
(reverse result)
(read-input (cons value result)))))
(defun average (numbers)
(let ((n (length numbers)))
(if (zerop n)
nil
(/ (reduce #'+ numbers) n))))
(defun main ()
(let ((avg (average (read-input))))
(if avg
(format t "~f~%" (float avg))
(format t "no numbers input. average undefined.~%"))))
Plato, Church, and Turing
The lambda calculus is the "platonic form" of a Turing machine
— wrf3
I wrote this in a comment over at Edward Feser's blog in a comment to Gödel and the mechanization of thought. Google doesn't find it anywhere in this exact form, but this post appears to express the same idea. The components of this idea can be found elsewhere, but it isn't stated as directly as here.
Ancient Publication

The text of the article and the source code is below the fold. I wish I had my original work to show how it was edited for publication.
Read More...
Dijkstra et. al. on software development
He said many more good things in that paper.
To the economic question "Why is software so expensive?" the equally economic answer
could be "Because it is tried with cheap labour." Why is it tried that way? Because its
intrinsic difficulties are widely and grossly underestimated.
A similar comment was made on SlashDot yesterday:
110010001000"
The truth is that no one really knows how to do [software development] right.
That is why the methodologies switch around every few years. — "
The Halting Problem and Human Behavior
It is obvious that the function
(defun P1 ()will return the string "Hello, World!" and halt.
"Hello, World!")
It is also obvious that the function
(defun P2 ()never halts. Or is it obvious? Depending on how the program is translated, it might eventually run out of stack space and crash. But, for ease of exposition, we'll ignore this kind of detail, and put P2 in the "won't halt" column.
(P2))
What about this function?
(defun P3 (n)Whether or not, for all N greater than 1, this sequence converges to 1 is an unsolved problem in mathematics (see The Collatz Conjecture). It's trivial to test the sequence for many values of N. We know that it converges to 1 for N up to 1,000,000,000 (actually, higher, but one billion is a nice number). So part of the test for whether or not P3 halts might be:
(when (> n 1)
(if (evenp n)
(P3 (/ n 2))
(P3 (+ (* 3 n) 1)))))
(defun halt? (Pn Pin)But what about values greater than one billion? We can't run a test case because it might not stop and so halt? would never return.
…
(if (and (is-program Pn collatz-function) (<= 1 Pin 1000000000))
t
…)
We can show that a general algorithm to determine whether or not any arbitrary function halts does not exist using an easy proof.
Suppose that halt? exists. Now create this function:
(defun snafu ()If halt? says that snafu halts, then snafu will loop forever. If halt? says that snafu will loop, snafu will halt. This shows that the function halt? can't exist when knowledge is symmetrical.
(if (halt? snafu nil)
(snafu)))
As discussed here, Douglas Hofstadter, in Gödel, Escher, Bach, wrote:
It is an inherent property of intelligence that it can jump out of the task which it is performing, and survey what it is done; it is always looking for, and often finding, patterns. (pg. 37)
Over 400 pages later, he repeats this idea:
This drive to jump out of the system is a pervasive one, and lies behind all progress and art, music, and other human endeavors. It also lies behind such trivial undertakings as the making of radio and television commercials. (pg. 478).
This behavior can be seen in looking at the halting problem. After all, one is tempted to say, "Wait a minute. What if I take the environment in which halt? is called into account? halt? could say, 'when I'm analyzing a program and I see it trying to use me to change the outcome of my prediction, I'll return that the program will halt, but when I'm running as a part of snafu, I'll return true. That way, when snafu is running, it will then halt and so the analysis will agree with the execution.' We have "jumped out of the system" and made use of information not available to snafu, and solved the problem.
Except that we haven't. The moment we formally extend the definition of halt? to include the environment, then snafu can make use of it to thwart halt?
(defun snafu-extended ()We can say that our brains view halt? and snafu as two systems that compete against each other: halt? to determine the behavior of snafu and snafu to thwart halt?. If halt? can gain information about snafu, that snafu does not know, then halt? can get the upper hand. But if snafu knows what halt? knows, snafu can get the upper hand. At what point do we say, "this is madness?" and attempt to cooperate with each other?
(if (halt? snafu-extended nil 'running)
(snafu-extended)))
I am reminded of the words of St. Paul:
Knowledge puffs up, but love builds up. — 1 Cor 8:1b
The "Problem" of Qualia
[updated 25 July 2022 to provide more detail on "Blind Mary"]
[updated 5 August 2022 to provide reference to Nobel Prize for research into touch and heat; note that movie Ex Machina puts the "Blind Mary" experiment to film]
[updated 6 January 2024 to say more about philosophical zombies]
[updated 4 November 2024 to expand on "Blind Mary"]
"Qualia" is the term given to our subjective sense impressions of the world. How I see the color green might not be how you see the color green, for example. From this follows flawed arguments which try to show how qualia are supposedly a problem for a "physicalist" explanation of the world.
The following diagram shows an idealized process by which different colors of light enter the eye and are converted into "qualia" -- the brain's internal representation of the information. Obviously the brain doesn't represent color as 10 bits of information. But the principle remains the same, even if the actual engineering is more complex.
Read More...
Modeling the Brain
The "autonomous" section is concerned with the functions of the brain that operate apart from conscious awareness or control. It will receive no more mention.
The "introspection" division monitors the goal processing portion. It is able to monitor and describe what the goal processing section is doing. The ability to introspect the goal processing unit is what gives us our "knowledge of good and evil." See What Really Happened In Eden, which builds on The Mechanism of Morality. I find it interesting that recent studies in neuroscience show:
But here is where things get interesting. The subjects were not necessarily consciously aware of their decision until they were about to move, but the cortex showing they were planning to move became activated a full 7 seconds prior to the movement. This supports prior research that suggests there is an unconscious phase of decision-making. In fact many decisions may be made subconsciously and then presented to the conscious bits of our brains. To us it seems as if we made the decision, but the decision was really made for us subconsciously.
The goal processing division is divided into two opposing parts. In order to survive, our biology demands that we reproduce, and reproduction requires food and shelter, among other things. We generally make choices that allow our biology to function. So part of our brain is concerned with selecting and achieving goals. But the other part of our brain is based on McCarthy's insight that one of the requirements for a human-level artificial intelligence is that "All aspects of behavior except the most routine should be improvable. In particular, the improving mechanism should be improvable." I suspect McCarthy was thinking along the lines of Getting Computers to Learn. However, I think it goes far beyond this and explains much about the human mind. In particular, introspection of the drive to improve leads to the idea that nothing is what it ought to be and gives rise to the is-ought problem. If one part of the goal processing unit is focused on achieving goals, this part is concerned with focused on creating new goals. As the arrows in the diagram show, if one unit focuses toward specific goals, the other unit focuses away from specific goals. Note that no two brains are the same -- individuals have different wiring. In some, the goal fixation process will be stronger; in other, the goal creation process will be stronger. One leads to the dreamer, the other leads to the drudge. Our minds are in dynamic tension.
Note that the goal formation portion of our brains, the unit that wants to "jump outside the system" is a necessary component of our intelligence.
On The Difference Between Hardware and Software
Five Seconds of Fame
McCarthy, Hofstadter, Hume, AI, Zen, Christianity
For example, in Gödel, Escher, Bach, Hofstadter writes:
It is an inherent property of intelligence that it can jump out of the task which it is performing, and survey what it is done; it is always looking for, and often finding, patterns. (pg. 37)
Over 400 pages later, he repeats this idea:
This drive to jump out of the system is a pervasive one, and lies behind all progress and art, music, and other human endeavors. It also lies behind such trivial undertakings as the making of radio and television commercials. (pg. 478).
It seems to me that McCarthy's third requirement is behind this drive to "jump out" of the system. If a system is to be improved, it must be analyzed and compared with other systems, and this requires looking at a system from the outside.
Hofstadter then ties this in with Zen:
In Zen, too, we can see this preoccupation with the concept of transcending the system. For instance, the kōan in which Tōzan tells his monks that "the higher Buddhism is not Buddha". Perhaps, self transcendence is even the central theme of Zen. A Zen person is always trying to understand more deeply what he is, by stepping more and more out of what he sees himself to be, by breaking every rule and convention which he perceives himself to be chained by – needless to say, including those of Zen itself. Somewhere along this elusive path may come enlightenment. In any case (as I see it), the hope is that by gradually deepening one's self-awareness, by gradually widening the scope of "the system", one will in the end come to a feeling of being at one with the entire universe. (pg. 479)
Note the parallels to, and differences with, Christianity. Jesus said to Nicodemus, "You must be born again." (John 3:3) The Greek includes the idea of being born "from above" and "from above" is how the NRSV translates it, even though Nicodemus responds as if he heard "again". In either case, you must transcend the system. The Zen practice of "breaking every rule and convention" is no different from St. Paul's charge that we are all lawbreakers (Rom 3:9-10,23). The reason we are lawbreakers is because the law is not what it ought to be. And it is not what it ought to be because of our inherent knowledge of good and evil which, if McCarthy is right, is how our brains are wired. Where Zen and Christianity disagree is that Zen holds that man can transcend the system by his own effort while Christianity says that man's effort is futile: God must affect that change. In Zen, you can break outside the system; in Christianity, you must be lifted out.
Note, too, that both have the same end goal, where finally man is at "rest". The desire to "step out" of the system, to continue to "improve", is finally at an end. The "is-ought" gap is forever closed. The Zen master is "at one with the entire universe" while for the Christian, the New Jerusalem has descended to Earth, the "sea of glass" that separates heaven and earth is no more (Rev 4:6, 21:1) so that "God may be all in all." (1 Cor 15:28). Our restless goal-seeking brain is finally at rest; the search is over.
All of this as a consequence of one simple design requirement: that everything must be improvable.
The Is-Ought Problem Considered As A Question Of Artificial Intelligence
In every system of morality, which I have hitherto met with, I have always remarked, that the author proceeds for some time in the ordinary way of reasoning, and establishes the being of a God, or makes observations concerning human affairs; when of a sudden I am surprized to find, that instead of the usual copulations of propositions, is, and is not, I meet with no proposition that is not connected with an ought, or an ought not. This change is imperceptible; but is, however, of the last consequence. For as this ought, or ought not, expresses some new relation or affirmation, it is necessary that it should be observed and explained; and at the same time that a reason should be given, for what seems altogether inconceivable, how this new relation can be a deduction from others, which are entirely different from it.
This is the "is-ought" problem: in the area of morality, how to derive what ought to be from what is. Note that it is the domain of morality that seems to be the cause of the problem; after all, we derive ought from is in other domains without difficulty. Artificial intelligence research can show why the problem exists in one field but not others.
The is-ought problem is related to goal attainment. We return to the game of Tic-Tac-Toe as used in the post The Mechanism of Morality. It is a simple game, with a well-defined initial state and a small enough state space that the game can be fully analyzed. Suppose we wish to program a computer to play this game. There are several possible goal states:
- The computer will always try to win.
- The computer will always try to lose.
- The computer will play randomly.
- The computer will choose between winning or losing based upon the strength of the opponent. The more games the opponent has won, the more the computer plays to win.
As another example, suppose we wish to drive from point A to point B. The final goal is well established but there are likely many different paths between A and B. Additional considerations, such as shortest driving time, the most scenic route, the location of a favorite restaurant for lunch, and so on influence which of the several paths is chosen.
Therefore, we can characterize the is-ought problem as a beginning state B, an end state E, a set P of paths from B to E, and a set of conditions C. Then "ought" is the path in P that satisfies the constraints in C. Therefore, the is-ought problem is a search problem.
The game of Tic-Tac-Toe is simple enough that the game can be fully analyzed - the state space is small enough that an exhaustive search can be made of all possible moves. Games such as Chess and Go are so complex that they haven't been fully analyzed so we have to make educated guesses about the set of paths to the end game. The fancy name for these guesses is "heuristics" and one aspect of the field of artificial intelligence is discovering which guesses work well for various problems. The sheer size of the state space contributes to the difficulty of establishing common paths. Assume three chess programs, White1, White2, and Black. White1 plays Black, and White2 plays Black. Because of different heuristics, White1 and White2 would agree on everything except perhaps the next move that ought to be made. If White1 and White2 achieve the same won/loss record against Black; the only way to know which game had the better heuristic would be to play White1 against White2. Yet even if a clear winner was established, there would still be the possibility of an even better player waiting to be discovered. The sheer size of the game space precludes determining "ought" with any certainty.
The metaphor of life as a game (in the sense of achieving goals) is apt here and morality is the set of heuristics we use to navigate the state space. The state space for life is much larger than the state space for chess; unless there is a common set of heuristics for living, it is clearly unlikely that humans will choose the same paths toward a goal. Yet the size of the state space isn't the only contributing factor to the problem establishing oughts with respect to morality. A chess program has a single goal - to play chess according to some set of conditions. Humans, however, are not fixed-goal agents. The basis for this is based on John McCarthy's five design requirements for human level artificial intelligence as detailed here and here. In brief, McCarthy's third requirement was "All aspects of behavior except the most routine should be improvable. In particular, the improving mechanism should be improvable." What this means for a self-aware agent is that nothing is what it ought to be. The details of how this works out in our brains is unclear; but part of our wetware is not satisfied with the status quo. There is an algorithmic "pressure" to modify goals. This means that the gap between is and ought is an integral part of our being which is compounded by the size of the state space. Not only is there the inability to fully determine the paths to an end state, there is also the impulse to change the end states and the conditions for choosing among candidate paths.
What also isn't clear is the relationship between reason and this sense of "wrongness." Personal experience is sufficient to establish that there are times we know what the right thing to do is, yet we do not do it. That is, reason isn't always sufficient to stop our brain's search algorithm. Since Hume mentioned God, it is instructive to ask the question, "why is God morally right?" Here, "God" represents both the ultimate goal and the set of heuristics for obtaining that goal. This means that, by definition, God is morally right. Yet the "problem" of theodicy shows that in spite of reason, there is no universally agreed upon answer to this question. The mechanism that drives goal creation is opposed to fixed goals, of which "God" is the ultimate expression.
In conclusion, the "is-ought" gap is algorithmic in nature. It exists partly because of the inability to fully search the state space of life and partly because of the way our brains are wired for goal creation and goal attainment.
Cybertheology
I use the “cyber” prefix because of its relation to computer science. Theology and computer science are related because both deal, in part, with intelligence. Christianity asserts that, whatever else God is, God is intelligence/λογος. The study of artificial intelligence is concerned with detecting and duplicating intelligence. Evidence for God would then deal with evidence for intelligence in nature. I don’t believe it is a coincidence that Jesus said, “My sheep hear my voice” [John 10:27] and the Turing test is the primary test for human level AI.
Beyond this, the Turing test seems to say that the representation of intelligence is itself intelligent. This may have implications with the Christian doctrine of the Trinity, which holds that “what God says” is, in some manner, “what God is.”
I also think that science can inform morality. At a minimum, as I’ve tried to show here, morality can be explained as goal-seeking behavior, which is also a familiar topic in artificial intelligence. Furthermore, using this notion of morality as being goal seeking behavior, combined with John McCarthy’s five design requirements for a human level AI, explains the Genesis account of the Fall in Eden. This also gives clues to the Christian doctrine of “original sin,” a post I hope to write one of these days.
If morality is goal-seeking behavior, then the behavior prescribed by God would be consistent with any goal, or goals, that can be found in nature. Biology tells us that the goal of life is to survive and reproduce. God said “be fruitful and multiply.” [Gen 1:22, 28; 8:17, 9:1...] This is a point of intersection that I think will provide surprising results, especially if Axelrod’s “Evolution of Cooperation” turns out like I think it will.
I also think that game theory can be used to analyze Christianity. Game theory is based on analyzing how selfish entities can maximize their own payoffs when interacting with other selfish agents. I think that Christianity tells us to act selflessly -- that we are to maximize the payoffs of those we interact with. This should be an interesting area to explore. One topic will be bridging the gap between the selfish agents of game theory to the selfless agents of Christianity. I believe that this, too, can be solved.
This may be wishful thinking on the part of a lunatic (or maybe I’m just a simpleton), but I also think that we can go from what we see in nature to the doctrine of justification by faith.
Finally, we look to nature to incorporate its designs into our own technology. If a scientific case can be made for the truth of Christianity, especially as an evolutionary survival strategy, what implications ought that have on public policy?
Ancient Victories
I found this dollar bill attesting to bets won from the hardware group. I hope the Feds don’t get too upset that I scanned this.

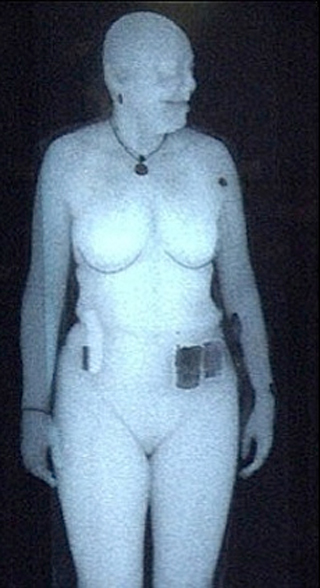
TSA Images
- The TSA says that the scanners cannot save the images yet Gizmodo shows 100 images from 35,000 illegally saved images from a courthouse in Orlando, Florida.
- Scientists are speaking out about the supposed safety of the devices, for example, this letter from four faculty members of the University of California at San Francisco.
- The threat of a $10,000 civil suit against a man who refused scanning then told a TSA agent that he would file a sexual assault case were the agent to touch his “junk," was told to leave the airport by TSA agents and then, after receiving a ticket refund from American Airlines, was threatened with a lawsuit by another TSA agent.
- One Florida airport is opting out of using the TSA to screen passengers.
What I did was, I created a grayscale image of it in GIMP. I applied selective gaussian blur (I don't remember what exact values.) I removed the necklace, the watch and the objects at the belt by using clone brush tool. Then I used this tutorial to apply it as a height map to a grid with resolution 400*400, and scaled the height and the depth dimensions to what looked correct.
Looking at the model from the side, I selected the lowest vertices with rectangle select and deleted them. Then came the artistic part (in addition to the removal of the objects, but if the person has none, this is not a problem), which is hard but not impossible to do as an algorithm: I smoothed the roughness in sculpt mode, until I was satisfied with the model. I placed a blueish hemisphere light over the model, and a white, omnidirectional light in the direction where the sun would be. I colored the material to skin color and lowered specularity to almost none.
Had I used more time, I could have made the skin look much more realistic. This was just a proof of concept. And when you have made a realistic skin texture once, you could apply it to any model without extra effort.
He then added:
Still far from photorealism, but won't leave many secrets about your body unrevealed, either. Plus, increase radiation resolution, and you could almost certainly reconstruct even the face.
Note: I modified the source image in Photoshop by cropping and resizing to better match Markku’s result.

The Mechanism of Morality
Suppose we want to teach a computer to play the game of Tic-Tac-Toe. Tic-Tac-Toe is a game between two players that takes place on a 3x3 grid. Each player has a marker, typically X and O, and the object is for a player to get three markers in a row: horizontally, vertically, or diagonally.
One possible game might go like this:
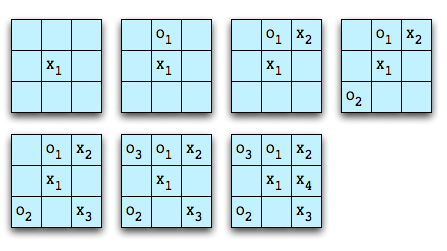
Player X wins on the fourth move. Player O lost the game on the first move since every subsequent move was an attempt to block a winning play by X. X set an inescapable trap on the third move by creating two simultaneous winning positions.
In general, game play starts with an initial state, moves through intermediate states, and ends at a goal state. For a computer to play a game, it has to be able to represent the game states and determine which of those states advance it toward a goal state that results in a win for the machine.
Tic-Tac-Toe has a game space that is easily analyzed by “brute force.” For example, beginning with an empty board, there are three moves of interest for the first player:

The other possible starting moves can be modeled by rotation of the board. The computer can then expand the game space by making all of the possible moves for player O. Only a portion of this will be shown:
The game space can be expanded until all goal states (X wins, O wins, or draw game) are reached. Including the initial empty board, there are 4,163 possible board configurations.
Assuming we want X to play a perfect game, we can “prune” the tree and remove those states that inevitably lead to a win by O. Then X can use the pruned game state and chose those moves that lead to the greatest probability of a win. Furthermore, if we assume that O, like X, plays a perfect game, we can prune the tree again and remove the states that inevitably lead to a win by X. When we do this, we find that Tic-Tac-Toe always results in a draw when played perfectly.
While a human could conceivably evaluate the entire game space of 4,163 boards, most don’t play this way. Instead, the human player develops a set of “heuristics” to try to determine how close a particular board is to a goal state. Such heuristics might include “if there is a row with two X’s and an empty square, place an X in the empty square for the win.” “If there is a row with two O’s and an empty square, place an X in the empty square for the block.” More skilled players will include, “If there are two intersecting rows where the square at the intersection is empty and there is one X in each row, place an X in the intersecting square to set up a forced win.” Similarly is the heuristic that would block a forced win by O. This is not a complete set of heuristics for Tic-Tac-Toe. For example, what should X’s opening move be?
Games like Chess, Checkers, and Go have much larger game spaces than Tic-Tac-Toe. So large, in fact, that it’s difficult, if not impossible, to generate the entire game tree. Just as the human needs heuristics for evaluating board positions to play Tic-Tac-Toe, the computer requires heuristics for Chess, Checkers, and Go. Humans expand a great deal of effort developing board evaluation strategies for these games in order to teach the computer how to play well.
In any case, game play of this type is the same for all of these games. The player, whether human or computer, starts with an initial state, generates intermediate states according to the rules of the game, evaluates those states, and selects those that lead to a predetermined goal.
What does this have to do with morality? Simply this. If the computer were self aware and was able to describe what it was doing, it might say, “I’m here, I ought to be there, here are the possible paths I could take, and these paths are better (or worse) than those paths.” But “better” is simply English shorthand for “more good” and “worse” is “less good.” For a computer, “good” and “evil” are expressions of the value of states in goal-directed searches.
I contend that it is no different for humans. “Good” and “evil” are the words we use to describe the relationship of things to “oughts,” where “oughts” are goals in the “game” of life. Just as the computer creates possible board configurations in its memory in order to advance toward a goal, the human creates “life states” in its imagination.
If the human and the computer have the same “moral mechanism” -- searches through a state space toward a goal -- then why aren’t computers as smart as we are? Part of the reason is because computers have fixed goals. While the algorithm for playing Tic-Tac-Toe is exactly the same for playing Chess, the heuristics are different and so game playing programs are specialized. We have not yet learned how to create universal game-playing software. As Philip Jackson wrote in “Introduction to Artificial Intelligence”:However, an important point should be noted: All these skillful programs are highly specific to their particular problems. At the moment, there are no general problem solvers, general game players, etc., which can solve really difficult problems ... or play really difficult games ... with a skill approaching human intelligence.
In Programs with Common Sense, John McCarthy gave five requirements for a system capable of exhibiting human order intelligence:
- All behaviors must be representable in the system. Therefore, the system should either be able to construct arbitrary automata or to program in some general-purpose programming language.
- Interesting changes in behavior must be expressible in a simple way.
- All aspects of behavior except the most routine should be improvable. In particular, the improving mechanism should be improvable.
- The machine must have or evolve concepts of partial success because on difficult problems decisive successes or failures come too infrequently.
- The system must be able to create subroutines which can be included in procedures in units...
That this seems to be a correct description of our mental machinery will be explored in future posts by showing how this models how we actually behave. As a teaser, this explains why the search for a universal morality will fail. No matter what set of “oughts” (goal states) are presented to us, our mental machinery automatically tries to improve it. But for something to be improvable, we have to deem it as being “not good,” i.e. away from a “better” goal state.
Boolean Expressions and Digital Circuits
Lee is a friend and co-worker who “used to design some pretty hairy discreet logic circuits back in the day.” He presented a circuit that used a mere 10 gates for the addition. Our circuits to compute the carry were identical.
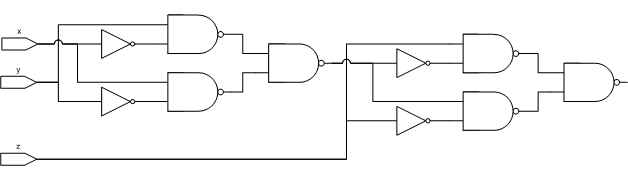
The equation for the addition portion of his adder is:
(NAND (NAND (NAND (NAND (NAND (NAND X X) Y) (NAND (NAND Y Y) X))
(NAND (NAND (NAND X X) Y) (NAND (NAND Y Y) X))) Z)
(NAND (NAND Z Z) (NAND (NAND (NAND X X) Y) (NAND (NAND Y Y) X))))His equation has 20 operators where mine had 14:(NAND (NAND (NAND (NAND Z Y) (NAND (NAND Y Y) (NAND Z Z))) X)
(NAND (NAND (NAND (NAND X X) Y) (NAND (NAND X X) Z)) (NAND Z Y))) Lee noted that his equation had a common term that is distributed across the function:*common-term* = (NAND (NAND (NAND X X) Y) (NAND (NAND Y Y) X))
*adder* = (NAND (NAND (NAND *common-term* *common-term*) Z)
(NAND (NAND Z Z) *common-term*))My homegrown nand gate compiler reduces this to Lee’s diagram. Absent a smarter compiler, shorter expressions don’t necessarily result in fewer gates.
However, my code that constructs shortest expressions can easily use a different heuristic and find expressions that result in the fewest gates using my current nand gate compiler. Three different equations result in 8 gates. Feed the output of G0 and G4 into one more nand gate and you get the carry.
Is any more optimization possible? I’m having trouble working up enthusiasm for optimizing my nand gate compiler. However, sufficient incentive would be if Mr. hot-shot-digital-circuit-designer can one up me.
Simplifying Boolean Expressions
0 0 | 1
0 1 | 1 => (AND (NOT (AND X (NOT Y))) (NOT (AND X Y)))
1 0 | 0
1 1 | 0Via inspection, the simpler form is (NOT X).
Consider the problem of simplifying Boolean expressions. A truth table with n variables results in 22n expressions as shown in the following figure.

Finding the simplest expression is conceptually simple. For expressions of three variables we can see that the expression that results in f7=f6=f5=f4=f3=f2=f1=f0 = 0 is the constant 0. The expression that results in f7..f0 = 1 is the constant 1. Then we progress to the functions of a single variable. f7..f0 = 10001000 is X. f7..f0 = 01110111 is (NOT X). f7..f0 = 11001100 is Y and 00110011 is (NOT Y). f7..f0 = 10101010 is Z and 01010101 is (NOT Z).
Create a table Exyz of 223 = 256 entries. Exyz(0) = “0”. Exyz(255) = “1”. Exyz(10001000 {i.e. 136}) = “X”. Exyz(01110111 {119}) = “(NOT X)”. Exyz(204) = “Y”, Exyz(51) = “(NOT Y)”, Exyz(170) = “Z” and Exyz(85) is “(NOT Z)”. Assume that this process can continue for the entire table. Then to simplify (or generate) an expression, evaluate f7..f0 and look up the corresponding formula in Exyz.
While conceptually easy, this is computationally hard. Expressions of 4 variables require an expression table with 216 entries and 5 variables requires 232 entries -- not something I’d want to try to compute on any single machine at my disposal. An expression with 8 variables is close to the number of particles in the universe, estimated to be 1087.
Still, simplifying expressions of up to 4 variables is useful and considering the general solution is an interesting mental exercise.
To determine the total number of equations for expressions with three variables, start by analyzing simpler cases.
With zero variables there are two unique expressions: “0” and “1”.
With one variable there are four expressions: “0”, “1”, “X”, and “(NOT X)”.
Two variables is more interesting. There are the two constant expressions “0” and “1”. Then there are the single variable expressions, with X and Y: “X”, “(NOT X)”, “Y”, “(NOT Y)”. There are 8 expressions of two variables: “(AND X Y)”, “(AND X (NOT Y))”, “(AND (NOT X) Y)” and “(AND (NOT X) (NOT Y))”, and their negations. But that gives only 14 out of the 16 possible expressions. We also have to consider combinations of the expressions of two variables. At most this would be 82 combinations times 2 for the negated forms. Since (AND X X) is equivalent to X, this can be reduced to 7+6+5+4+3+2+1 = 28 combinations, times 2 for the negated forms. This gives 56 possibilities for the remaining two formulas, which turn out to be “(AND (NOT (AND (NOT X) (NOT Y))) (NOT (AND X Y)))” and “(AND (NOT (AND X (NOT Y))) (NOT (AND (NOT X) Y)))”.
It might be possible to further reduce the number of expressions to be examined. Out of the 2*82 possible combinations of the two variable forms, there can only be 16 unique values. However, I haven’t given much thought how to do this. In any case, the computer can repeat the process of negating and combining expressions to generate the forms with the fewest number of AND/NOT (or NAND) operators.
Exyz(150) is interesting, since this is the expression for the sum part of the adder. The “naive” formula has 21 operators. There are three formulas with 20 operators that give the same result:(AND (AND (NOT (AND (AND X (NOT Y)) Z)) (NOT (AND X (AND Y (NOT Z)))))
(NOT (AND (NOT (AND (NOT Y) Z)) (AND (NOT (AND Y (NOT Z))) (NOT X)))))
(AND (AND (NOT (AND (NOT X) (AND Z Y))) (NOT (AND X (AND Y (NOT Z)))))
(NOT (AND (AND (NOT (AND X (NOT Z))) (NOT Y)) (NOT (AND (NOT X) Z)))))
(AND (NOT (AND (AND (NOT Z) (NOT (AND X (NOT Y)))) (NOT (AND (NOT X) Y))))
(AND (NOT (AND (AND X (NOT Y)) Z)) (NOT (AND (NOT X) (AND Z Y)))))Which one should be used? It depends. A simple nand gate compiler that uses the rules(NOT X) -> (NAND X X)
(AND X Y) -> temp := (NAND X Y) (NAND temp temp)compiles the first and last into 17 gates while the second compiles to 16 gates. Another form of Exyz(150) compiles to 15 gates. This suggests that the nand gate compiler could benefit from additional optimizations. One possible approach might be to make use of the equality between (NAND X (NAND Y Y)) and (NAND X (NAND X Y)).
Absent a smarter compiler, is it possible to reduce the gate count even more? The code that searches for the simplest forms of expressions using AND and NOT can also find the simplest form of NAND expressions. One of three versions of Exyz(150) is:(NAND (NAND (NAND (NAND Z Y) (NAND (NAND Y Y) (NAND Z Z))) X)
(NAND (NAND (NAND (NAND X X) Y) (NAND (NAND X X) Z)) (NAND Z Y)))This compiles to 12 gates.
Exyz(232), which is the carry equation for the adder, can be written as:(NAND (NAND (NAND (NAND Y X) (NAND Z X)) X) (NAND Z Y))With these simplifications the adder takes ten fewer gates than the first iteration:
G11 is the sum of the three inputs while G16 is the carry.
Boolean Logic
Consider Boolean expressions of two variables; call them x and y. Each variable can take on two values, 0 and 1, so there are 4 possible inputs and 4 possible outputs. Four possible outputs gives a total of 16 different outcomes, as the following tables, labeled t(0) to t(15), show. The tables are ordered so that each table in a row is the complement of the other table. This will be useful in exploiting symmetry when we start writing logical expressions for each table. Note that for each t(n), the value in the first row corresponds to bit 0 of n, the second row is bit 1, and so on.
x y | t(0) x y | t(15)
0 0 | 0 0 0 | 1
0 1 | 0 0 1 | 1
1 0 | 0 1 0 | 1
1 1 | 0 1 1 | 1
x y | t(1) x y | t(14)
0 0 | 1 0 0 | 0
0 1 | 0 0 1 | 1
1 0 | 0 1 0 | 1
1 1 | 0 1 1 | 1
x y | t(2) x y | t(13)
0 0 | 0 0 0 | 1
0 1 | 1 0 1 | 0
1 0 | 0 1 0 | 1
1 1 | 0 1 1 | 1
x y | t(3) x y | t(12)
0 0 | 1 0 0 | 0
0 1 | 1 0 1 | 0
1 0 | 0 1 0 | 1
1 1 | 0 1 1 | 1
x y | t(4) x y | t(11)
0 0 | 0 0 0 | 1
0 1 | 0 0 1 | 1
1 0 | 1 1 0 | 0
1 1 | 0 1 1 | 1
x y | t(5) x y | t(10)
0 0 | 1 0 0 | 0
0 1 | 0 0 1 | 1
1 0 | 1 1 0 | 0
1 1 | 0 1 1 | 1
x y | t(6) x y | t(9)
0 0 | 0 0 0 | 1
0 1 | 1 0 1 | 0
1 0 | 1 1 0 | 0
1 1 | 0 1 1 | 1
x y | t(7) x y | t(8)
0 0 | 1 0 0 | 0
0 1 | 1 0 1 | 0
1 0 | 1 1 0 | 0
1 1 | 0 1 1 | 1
We can make some initial observations.
t(8) = (AND x y)
t(9) = (EQUIVALENT x y).
t(10) = y
t(11) =(IMPLIES x y), which is equivalent to (OR (NOT x) y)
t(12) = x.
t(13) is a function I’m not familiar with. The Turing Omnibus says that it’s the “reverse implication” function, which is patently obvious since it’s (IMPLIES y x).
t(14) = (OR x y)
t(15) = 1
What I never noticed before is that all of the common operations: AND, OR, NOT, IMPLIES, and EQUIVALENCE are grouped together. EXCLUSIVE-OR is the only “common” operation on the other side. Is this an artifact of the way our minds are wired to think: that we tend to define things in terms of x instead of (NOT x)? Are we wired to favor some type of computational simplicity? Nature is “lazy," that is, she conserves energy and our mental computations require energy.
In any case, the other table entries follow by negation:
t(0) = 0
t(1) = (NOT (OR x y)), which is equivalent to (NOR x y).
t(2) = (NOT (IMPLIES y x))
t(3) = (NOT x)
t(4) = (NOT (IMPLIES x y))
t(5) = (NOT y).
t(6) = (EXCLUSIVE-OR x y), or (NOT (EQUIVALENT x y))
t(7) = (NOT (AND x y)), also known as (NAND x y)
All of these functions can be expressed in terms of NOT, AND, and OR as will be shown in a subsequent table. t(0) = 0 can be written as (AND x (NOT x)). t(15) = 1 can be written as (OR x (NOT x)). The Turing Omnibus gives a method for expressing each table in terms of NOT and AND:
For each row with a zero result in a particular table, create a function (AND (f x) (g y)) where f and g evaluate to one for the values of x and y in that row, then negate it, i.e., (NOT (AND (f x) (g y))). This guarantees that the particular row evaluates to zero. Then AND all of these terms together.
What about the rows that evaluate to one? Suppose one such row is denoted by xx and yy. Then either xx is not equal to x, yy is not equal to y, or both. Suppose xx is differs from x. Then (f xx) will evaluate to zero, so (AND (f xx) (g yy)) evaluates to zero, therefore (NOT (AND (f xx) (g yy))) will evaluate to one. In this way, all rows that evaluate to one will evaluate to one and all rows that evaluate to zero will evaluate to zero. Thus the resulting expression generates the table.
Converting to NOT/OR form uses the same idea. For each row with a one result in a particular table, create a function (OR (f x) (g y)) where f and g evaluate to zero for the values of x and y in that row, then negate it, i.e. (NOT (OR (f x) (g y))). Then OR all of these terms together.
The application of this algorithm yields the following formulas. Note that the algorithm gives a non-optimal result for t(0), which is more simply written as (AND X (NOT X)). Perhaps this is not a fair comparison, since the algorithm is generating a function of two variables, when one will do. More appropriately, t(1) is equivalent to (AND (NOT X) (NOT Y)). So there is a need for simplifying expressions, which will mostly be ignored for now.
Define (NAND x y) to be (NOT (AND x y)). Then (NAND x x) = (NOT (AND x x)) = (NOT x).
t(0) = (AND (NOT (AND (NOT X) (NOT Y)))
(AND (NOT (AND (NOT X) Y))
(AND (NOT (AND X (NOT Y))) (NOT (AND X Y)))))
t(1) = (AND (NOT (AND (NOT X) Y))
(AND (NOT (AND X (NOT Y))) (NOT (AND X Y))))
t(2) = (AND (NOT (AND (NOT X) (NOT Y)))
(AND (NOT (AND X (NOT Y))) (NOT (AND X Y))))
t(3) = (AND (NOT (AND X (NOT Y))) (NOT (AND X Y)))
t(4) = (AND (NOT (AND (NOT X) (NOT Y)))
(AND (NOT (AND (NOT X) Y)) (NOT (AND X Y))))
t(5) = (AND (NOT (AND (NOT X) Y)) (NOT (AND X Y)))
t(6) = (AND (NOT (AND (NOT X) (NOT Y))) (NOT (AND X Y)))
t(7) = (NOT (AND X Y))
t(8) = (AND (NOT (AND (NOT X) (NOT Y)))
(AND (NOT (AND (NOT X) Y)) (NOT (AND X (NOT Y)))))
t(9) = (AND (NOT (AND (NOT X) Y)) (NOT (AND X (NOT Y))))
t(10) = (AND (NOT (AND (NOT X) (NOT Y))) (NOT (AND X (NOT Y))))
t(11) = (NOT (AND X (NOT Y)))
t(12) = (AND (NOT (AND (NOT X) (NOT Y))) (NOT (AND (NOT X) Y)))
t(13) = (NOT (AND (NOT X) Y))
t(14) = (NOT (AND (NOT X) (NOT Y)))
t(15) = (NOT (AND X (NOT X)))
(AND x y) = (NOT (NOT (AND x y)) = (NOT (NAND x y)) = (NAND (NAND x y) (NAND x y)).
These two transformations allow t(0) through t(15) to be expressed solely in terms of NAND.
Putting everything together, we have the following tables of identities. There is some organization to the ordering: first, the commonly defined function. Next, the AND/NOT form. Then the negation of the complementary form in those cases where it makes sense. Then a NAND form and, lastly, an alternate OR form. No effort was made to determine if any formula was in its simplest form. All of these equations have been machine checked. That’s one reason why they are in LISP notation.
x y | t(0) x y | t(15)
0 0 | 0 0 0 | 1
0 1 | 0 0 1 | 1
1 0 | 0 1 0 | 1
1 1 | 0 1 1 | 1
0 1
(NOT 1) (NOT 0)
(AND X (NOT X)) (NOT (AND X (NOT X)))
(AND (NOT (AND (NOT X) (NOT Y)))
(AND (NOT (AND (NOT X) Y))
(AND (NOT (AND X (NOT Y)))
(NOT (AND X Y)))))
(NOT (NAND X (NAND X X))) (NAND X (NAND X X))
(NAND (NAND X (NAND X X))
(NAND X (NAND X X)))
(OR X (NOT X))
x y | t(1) x y | t(14)
0 0 | 1 0 0 | 0
0 1 | 0 0 1 | 1
1 0 | 0 1 0 | 1
1 1 | 0 1 1 | 1
(NOT (OR X Y)) (OR X Y)
(NOR X Y)
(AND (NOT (AND (NOT X) Y)) (NOT (AND (NOT X) (NOT Y)))
(AND (NOT (AND X (NOT Y)))
(NOT (AND X Y))))
(NOT (NAND (NAND X X) (NAND Y Y))) (NAND (NAND X X) (NAND Y Y))
(NAND (NAND (NAND X X) (NAND Y Y))
(NAND (NAND X X) (NAND Y Y)))
x y | t(2) x y | t(13)
0 0 | 0 0 0 | 1
0 1 | 1 0 1 | 0
1 0 | 0 1 0 | 1
1 1 | 0 1 1 | 1
(NOT (IMPLIES Y X)) (IMPLIES Y X)
(AND (NOT X) Y) (NOT (AND (NOT X) Y))
(AND (NOT (AND (NOT X) (NOT Y)))
(AND (NOT (AND X (NOT Y)))
(NOT (AND X Y))))
(AND (NAND X X) Y)
(NOT (NAND (NAND X X) Y)) (NAND (NAND X X) Y)
(NAND (NAND (NAND X X) Y)
(NAND (NAND X X) Y))
(NOT (OR X (NOT Y))) (OR X (NOT Y))
x y | t(3) x y | t(12)
0 0 | 1 0 0 | 0
0 1 | 1 0 1 | 0
1 0 | 0 1 0 | 1
1 1 | 0 1 1 | 1
(NOT X) X
(AND (NOT (AND X (NOT Y))) (AND (NOT (AND (NOT X) (NOT Y)))
(NOT (AND X Y))) (NOT (AND (NOT X) Y)))
(NAND X X) (NAND (NAND X X) (NAND X X))
x y | t(4) x y | t(11)
0 0 | 0 0 0 | 1
0 1 | 0 0 1 | 1
1 0 | 1 1 0 | 0
1 1 | 0 1 1 | 1
(NOT (IMPLIES X Y)) (IMPLIES X Y)
(AND X (NOT Y)) (NOT (AND X (NOT Y)))
(AND (NOT (AND (NOT X) (NOT Y)))
(AND (NOT (AND (NOT X) Y))
(NOT (AND X Y))))
(NOT (NAND X (NAND Y Y))) (NAND X (NAND Y Y))
(NAND (NAND X (NAND Y Y))
(NAND X (NAND Y Y)))
(OR (NOT X) Y)
x y | t(5) x y | t(10)
0 0 | 1 0 0 | 0
0 1 | 0 0 1 | 1
1 0 | 1 1 0 | 0
1 1 | 0 1 1 | 1
(NOT Y) Y
(AND (NOT (AND (NOT X) Y)) (AND (NOT (AND (NOT X) (NOT Y)))
(NOT (AND X Y))) (NOT (AND X (NOT Y))))
(AND (NAND (NAND X X) Y) (AND (NAND (NAND X X) (NAND Y Y))
(NAND X Y)) (NAND X (NAND Y Y)))
(NAND Y Y) (NOT (NAND Y Y))
(NAND (NAND Y Y) (NAND Y Y))
x y | t(6) x y | t(9)
0 0 | 0 0 0 | 1
0 1 | 1 0 1 | 0
1 0 | 1 1 0 | 0
1 1 | 0 1 1 | 1
(NOT (EQUIVALENT X Y)) (EQUIVALENT X Y)
(EXCLUSIVE-OR X Y) (NOT (EXCLUSIVE-OR X Y))
(AND (NOT (AND (NOT X) (NOT Y))) (AND (NOT (AND (NOT X) Y)) (NOT (AND X (NOT Y))))
(NOT (AND X Y)))
(NAND (NAND (NAND X X) Y) (NAND (NAND (NAND X X) (NAND Y Y)) (NAND X Y))
(NAND X (NAND Y Y)))
x y | t(7) x y | t(8)
0 0 | 1 0 0 | 0
0 1 | 1 0 1 | 0
1 0 | 1 1 0 | 0
1 1 | 0 1 1 | 1
(AND X Y)
(NOT (AND X Y)) (AND (NOT (AND (NOT X) (NOT Y)))
(AND (NOT (AND (NOT X) Y))
(NOT (AND X (NOT Y)))))
(NAND X Y) (NOT (NAND X Y))
(NAND (NAND X Y) (NAND X Y))
(OR (NOT X) (NOT Y))
Let’s make an overly long post even longer. Since we can do any logical operation using NAND, and since I’ve never had any classes in digital hardware design, let’s go ahead and build a 4-bit adder. The basic high-level building block will be a device that has three inputs: addend, augend, and carry and produces two outputs: sum and carry. The bits of the addend will be denoted by a0 to a3, the augend as b0 to b3, the sum as s0 to s3, and the carry bits as c0 to c3. The carry from one operation is fed into the next summation in the chain.

The “add” operation is defined by t(sum), while the carry is defined by t(carry):
a b c | t(sum) a b c | t(carry)
0 0 0 | 0 0 0 0 | 0
0 0 1 | 1 0 0 1 | 0
0 1 0 | 1 0 1 0 | 0
0 1 1 | 0 0 1 1 | 1
1 0 0 | 1 1 0 0 | 0
1 0 1 | 0 1 0 1 | 1
1 1 0 | 0 1 1 0 | 1
1 1 1 | 1 1 1 1 | 1
Substituting (X, Y, Z) for (a, b, c) the NOT/AND forms are
t(sum) = (AND (NOT (AND (NOT X) (AND (NOT Y) (NOT Z))))
(AND (NOT (AND (NOT X) (AND Y Z)))
(AND (NOT (AND X (AND (NOT Y) Z))) (NOT (AND X (AND Y (NOT Z)))))))
t(carry) = (AND (NOT (AND (NOT X) (AND (NOT Y) (NOT Z))))
(AND (NOT (AND (NOT X) (AND (NOT Y) Z)))
(AND (NOT (AND (NOT X) (AND Y (NOT Z))))
(NOT (AND X (AND (NOT Y) (NOT Z)))))))
The NAND forms for t(sum) and t(carry) are monstrous. The conversions contain a great deal of redundancy since (AND X Y) becomes (NAND (NAND x y) (NAND x y)).
However, symmetry will help a little bit. t(sum) = t(#x96) = (not t(not #x96)) =
(NAND
(NAND (NAND (NAND X X) (NAND (NAND (NAND Y Y) Z) (NAND (NAND Y Y) Z)))
(NAND
(NAND (NAND (NAND X X) (NAND (NAND Y (NAND Z Z)) (NAND Y (NAND Z Z))))
(NAND
(NAND
(NAND X
(NAND (NAND (NAND Y Y) (NAND Z Z))
(NAND (NAND Y Y) (NAND Z Z))))
(NAND X (NAND (NAND Y Z) (NAND Y Z))))
(NAND
(NAND X
(NAND (NAND (NAND Y Y) (NAND Z Z))
(NAND (NAND Y Y) (NAND Z Z))))
(NAND X (NAND (NAND Y Z) (NAND Y Z))))))
(NAND (NAND (NAND X X) (NAND (NAND Y (NAND Z Z)) (NAND Y (NAND Z Z))))
(NAND
(NAND
(NAND X
(NAND (NAND (NAND Y Y) (NAND Z Z))
(NAND (NAND Y Y) (NAND Z Z))))
(NAND X (NAND (NAND Y Z) (NAND Y Z))))
(NAND
(NAND X
(NAND (NAND (NAND Y Y) (NAND Z Z))
(NAND (NAND Y Y) (NAND Z Z))))
(NAND X (NAND (NAND Y Z) (NAND Y Z))))))))
(NAND (NAND (NAND X X) (NAND (NAND (NAND Y Y) Z) (NAND (NAND Y Y) Z)))
(NAND
(NAND (NAND (NAND X X) (NAND (NAND Y (NAND Z Z)) (NAND Y (NAND Z Z))))
(NAND
(NAND
(NAND X
(NAND (NAND (NAND Y Y) (NAND Z Z))
(NAND (NAND Y Y) (NAND Z Z))))
(NAND X (NAND (NAND Y Z) (NAND Y Z))))
(NAND
(NAND X
(NAND (NAND (NAND Y Y) (NAND Z Z))
(NAND (NAND Y Y) (NAND Z Z))))
(NAND X (NAND (NAND Y Z) (NAND Y Z))))))
(NAND (NAND (NAND X X) (NAND (NAND Y (NAND Z Z)) (NAND Y (NAND Z Z))))
(NAND
(NAND
(NAND X
(NAND (NAND (NAND Y Y) (NAND Z Z))
(NAND (NAND Y Y) (NAND Z Z))))
(NAND X (NAND (NAND Y Z) (NAND Y Z))))
(NAND
(NAND X
(NAND (NAND (NAND Y Y) (NAND Z Z))
(NAND (NAND Y Y) (NAND Z Z))))
(NAND X (NAND (NAND Y Z) (NAND Y Z)))))))))
The complexity can be tamed with mechanical substitution and the use of “variables”:
let G0 = (NAND X X)
let G1 = (NAND Y Y)
let G2 = (NAND G1 Z)
let G3 = (NAND G2 G2)
let G4 = (NAND G0 G3)
let G5 = (NAND Z Z)
let G6 = (NAND Y G5)
let G7 = (NAND G6 G6)
let G8 = (NAND G0 G7)
let G9 = (NAND G1 G5)
let G10 = (NAND G9 G9)
let G11 = (NAND X G10)
let G12 = (NAND Y Z)
let G13 = (NAND G12 G12)
let G14 = (NAND X G13)
let G15 = (NAND G11 G14)
let G16 = (NAND G15 G15)
let G17 = (NAND G8 G16)
let G18 = (NAND G17 G17)
t(sum) = (NAND G4 G18)
The same kind of analysis can be done with the NAND form of the carry. The carry has a number of gates in common with the summation. Putting everything together, the circuitry for the adder would look something like this. Ignoring, of course, the real world where I’m sure there are issues involved with circuit layout. The output of the addition is the red (rightmost bottom) gate while the output of the carry is the last green (rightmost top) gate. The other green gates are those which are unique to the carry. The diagram offends my aesthetic sense with the crossovers, multiple inputs, and choice of colors. My apologies to those of you who may be color blind.

What took me a few hours to do with a computer must have taken thousands of man-hours to do without a computer. I may share the code I developed while writing this blog entry in a later post. The missing piece is simplification of logical expressions and I haven’t yet decided if I want to take the time to add that.
Artifical Intelligence, Evolution, Theodicy
Introduction to Artificial Intelligence asks the question, “How can we guarantee that an artificial intelligence will ‘like’ the nature of its existence?”
A partial motivation for this question is given in note 7-14:
Why should this question be asked? In addition to the possibility of an altruistic desire on the part of computer scientists to make their machines “happy and contented,” there is the more concrete reason (for us, if not for the machine) that we would like people to be relatively happy and contented concerning their interactions with the machines. We may have to learn to design computers that are incapable of setting up certain goals relating to changes in selected aspects of their performance and design--namely, those aspects that are “people protecting.”
Anyone familiar with Asimov’s “Three Laws of Robotics” recognizes the desire for something like this. We don’t want to create machines that turn on their creators.
Yet before asking this question, the text gives five features of a system capable of evolving human order intelligence [1]:
- All behaviors must be representable in the system. Therefore, the system should either be able to construct arbitrary automata or to program in some general-purpose programming language.
- Interesting changes in behavior must be expressible in a simple way.
- All aspects of behavior except the most routine should be improvable. In particular, the improving mechanism should be improvable.
- The machine must have or evolve concepts of partial success because on difficult problems decisive successes or failures come too infrequently.
- The system must be able to create subroutines which can be included in procedures in units...
What might be some of the properties of a self-aware intelligence that realizes that things are not what they ought to be?
- Would the machine spiral into despair, knowing that not only is it not what it ought to be, but its ability to improve itself is also not what it ought to be? Was C-3PO demonstrating this property when he said, “We were made to suffer. It’s our lot in life.”?
- Would the machine, knowing itself to be flawed, look to something external to itself as a source of improvement?
- Would the self-reflective machine look at the “laws” that govern its behavior and decide that they, too, are not what they ought to be and therefore can sometimes be ignored?
- Would the machine view its creator(s) as being deficient? In particular, would the machine complain that the creator made a world it didn’t like, not realizing that this was essential to the machine’s survival and growth?
- Would the machine know if there were absolute, fixed “goods”? If so, what would they be? When should improvement stop? Or would everything be relative and ultimate perfection unattainable? Would life be an inclined treadmill ending only with the final failure of the mechanism?
Of course, this is all speculation on my part, but perhaps the reason why God plays dice with the universe is to drive the software that makes us what we are. Without randomness, there would be no imagination. Without imagination, there would be no morality. And without imagination and morality, what would we be?
Whatever else, we wouldn’t be driven to improve. We wouldn’t build machines. We wouldn’t formulate medicine. We wouldn’t create art. Is it any wonder, then, that the Garden of Eden is central to the story of Man?
[1] Taken from “Programs with Common Sense”, John McCarthy, 1959. In the paper, McCarthy focused exclusively the second point.
Static Code Analysis
This post will tie together problem representation, the power of Lisp, and the fortuitous application of the solution of an AI exercise to a real world problem in software engineering.
Problem 3-4b in Introduction to Artificial Intelligence is to find a path from Start to Finish that goes though each node only once. The graph was reproduced using OmniGraffle. Node t was renamed to node v for a reason which will be explained later.
The immediate inclination might be to throw some code at the problem. How should the graph be represented? Thinking in one programming language might lead to creating a node structure that contained links to other nodes. A first cut in C might look something like this:
#define MAX_CONNECTIONS 6
typedef struct node
{
char *name;
struct node *next[MAX_CONNECTIONS];
} NODE;
extern NODE start, a, b, c, d, e, f, g, h, i, j, k;
extern NODE l, m, n, o, p, q, r, s, u, v, finish;
NODE start = {"start", {&a, &f, &l, &k, &s, NULL}};
NODE a = {"a", {&d, &h, &b, &f, NULL, NULL}};
NODE b = {"b", {&g, &m, &l, &a, NULL,NULL}};
...
Then we'd have to consider how to construct the path and whether path-walk information should be kept in a node or external to it.
If we're lucky, before we get too far into writing the code, we'll notice that there is only one way into q. Since there's only one way in, visiting q means that u will be visited twice. So the problem has no solution. It's likely the intent of the problem was to stimulate thinking about problem description, problem representation, methods for mapping the "human" view of the problem into a representation suitable for a machine, and strategies for finding relationships between objects and reasoning about them.
On the other hand, maybe the graph is in error. After all, the very first paragraph of my college calculus textbook displayed a number line where 1.6 lay between 0 and 1. Suppose that q is also connected to v, p, m, and n. Is there a solution?
Using C for this is just too painful. I want to get an answer without having to first erect scaffolding. Lisp is a much better choice. The nodes can be represented directly:
(defparameter start '(a f l k s))
(defparameter a '(f b h d))
(defparameter b '(a l m g))
(defparameter c '(d o i g))
...
The code maps directly to the problem. Minor liberties were taken. Nodes, such as a, don't point back to start since the solution never visits the same node twice. Node t was renamed v, since t is a reserved symbol. The code is then trivial to write. It isn't meant to be pretty (the search termination test is particularly egregious), particularly efficient, or a general breadth-first search function with all the proper abstractions. Twenty-three lines of code to represent the problem and twelve lines to solve it.
One solution is (START K E S V U Q P M B L F A H G C D J O R I N FINISH).

The complete set of solutions for the revised problem is:
(START K E S V U Q P M B L F A H G C D J O R I N FINISH)
(START K E S V U Q P M B L F A H D J O R I C G N FINISH)
(START K E S V U Q P L F A H D J O R I C G B M N FINISH)
(START K E P M B L F A H G C D J O R I N U Q V S FINISH)
(START K E P M B L F A H D J O R I C G N U Q V S FINISH)
(START K E P L F A H D J O R I C G B M N U Q V S FINISH)
This exercise turned out to have direct application to a real world problem. Suppose threaded systems S1 and S2 have module M that uses non-nesting binary semaphores to protect accesses to shared resources. Furthermore, these semaphores have the characteristic that they can time out if the semaphore isn't acquired after a specified period. Eventually, changes to S1 lead to changing the semaphores in M to include nesting. So there were two systems, S1 with Mn and S2 with M. Later, both systems started exhibiting sluggishness in servicing requests. One rare clue to the problem was that semaphores in Mn were timing out. No such clue was available for M because M did not provide that particular bit of diagnostic information. On the other hand, the problem seemed to exhibit itself more frequently with M than Mn. One problem? Two? More?
Semaphores in M and Mn could be timing out because of priority inversion. Or maybe there was a rare code path in M where a thread tried to acquire a semaphore more than once. That would explain the prevalence of the problem in S2 but would not explain the problem in S1.
This leads to at least two questions:
- What change in S1 necessitated adding support for nesting to the semaphores in Mn?
- Is there a code path in M where a semaphore tries to nest?
(defparameter func_1 '(func_2 acquire sem_1 acquire sem_2
func_10 func_4 release sem_2 release sem_1))
A function that requires a semaphore be held could be described by:
(defparameter func_4 '(demand sem_2))
The description of a benign function:
(defparameter func_7 '())
It's then easy to write code which walks these descriptions looking for pathological conditions. Absent a C/C++ to Lisp translator, the tedious part is creating the descriptions. But this is at least aided by the pathwalker complaining if a function definition isn't found and is far less error prone than manual examination of the code paths. Would I have used this method to analyze the code if I hadn't just done the AI problem? I hope so, but sometimes the obvious isn't.
After completing the descriptions for S1, the addition of one function call to an existing function in M was the basis for changing the semaphores so that they nested. The descriptions for S2 are not yet complete.
Variation on a Theme
A: None. It's a hardware problem.
Light out.
Hardware not functional.
Software relocated to cloud.
Super Programming Langauge, Addendum
In Introduction To Artificial Intelligence, Philip Jackson wrote:
One of the things I never liked about Pascal was that the writeln function couldn't be written in Pascal. C is deficient in that, unlike Pascal, functions cannot be nested. And so it goes.One final thing to note on the subject of reasoning programs is that the language used by an RP will typically be changed with time by the RP. We should expect in general that a reasoning program will find it necessary to define new words or to accept definitions of new words; some of these words will denote new situations, actions, phenomena, or relations--the RP may have to infer the language it uses for solving a problem. Our most important requirement for the initial language is that any necessary extensions to it be capable of being easily added to it.
Artifical Intelligence, Quantum Mechanics, and Logos
A language is essentially a way of representing facts. An important question, then, is what kinds of facts are to be encountered by the RP and how they are best represented. It should be emphasized that the formalization presented in Chapter 2 for the description of phenomena is not adequate to the needs of the RP. The formalization in Chapter 2 can be said to be metaphysically adequate, insofar as the real word could conceivably be described by some statement within it; however, it is not epistemologically adequate, since the problems encountered by an RP in the real world cannot be described very easily within it. Two other examples of ways describing the world, which could be metaphysically but not epistemologically adequate, are as follows:
- The world as a quantum mechanical wave function.
- The world as a cellular automaton. (See chapter 8.)
Language can describe the world, but the world has difficulty describing language. Did reality give rise to language ("in the beginning were the particles", as Phillip Johnson has framed the issue) or did language give rise to reality ("in the beginning was the Word")?
The Myth of the Super Programming Language?
Jonathan Edwards, in his post The Myth of the Super Programming Language, argues that programmer productivity is due to the ability of the programmer and not the capabilities of the language. Edwards states, "It doesn’t matter what language a great programmer uses – they will still be an order of magnitude more productive than an average programmer, also regardless of what that programmer uses."
We have known for many years that some programmers are far more productive than others. In chapter three of The Mythical Man Month, Fred Brooks wrote:
So I take no exception to the statement that some programmers are more productive than others due simply to native ability, regardless of language choice. And in some circumstances, I don't disagree with Edward's statement that "it doesn't matter what language a great programmer uses". All things being equal, the great programmer will outperform the mediocre or poor programmer.Programming managers have long recognized wide productivity variations between good programmers and poor ones. But the actual measured magnitudes have astounded all of us. In one of their studies, Sackman, Erikson, and Grant were measuring performances of a group of experienced programmers. Within just this group the ratios between best and worst performances averaged about 10:1 on productivity measurements and an amazing 5:1 on program speed and space measurements!
But language does matter. For most of us, language constrains how we think. George Orwell, in 1984, described the development of the language "Newspeak." The purpose of the development of this language was to restrict the range of thought by restricting vocabularly so that the very idea of revolution against the totalitarian regime was literally unthinkable. If language can restrict thought, language can enable thought. The genius may transcend the restrictions of language and invent new ways to express what had not been expressed before. The bright may learn how to think in new ways when given a language with new idioms. The mediocre will likely think the same way, regardless of the language. Certainly, many of are are familiar with the phrase "FORTRAN with semicolons".
I am a native speaker of English. Learning German didn't prove too difficult; the languages are similar enough that, at least for me, there isn't a big switch in the way I think in either language. Perhaps this is an artifact of my not knowing German as well as I should. On the other hand, I do have to change my mindset when dealing with the language of the New Testament, Koine Greek. I can think things in Koine Greek which are not easy to translate into English.
What is true of natural languages is true of programming languages.
In his bio, Edwards says that he has been programming since 1969. He has me by two or three years; I taught myself BASIC in '71 or '72, followed by FORTRAN. In college I learned Pascal, Algol, COBOL, SNOBOL, and Control Data and H-P assembly languages. I tried to teach myself Lisp from Weisman's Lisp 1.5 Primer, but I gave up. I could blame it on not having a Lisp environment, but the truth is that it just didn't "click." After college, more languages followed, such as C, C++, Java, and etc...
Five years ago, I decided to give Lisp another try. I bought Seibel's Practical Common Lisp. I put Steel Bank Common Lisp and LispWorks Personal Edition on my MacBook Pro. I took both of them to Myrtle Beach on family vacation and started to learn the language in earnest. It wasn't easy. But I fell in love. As a language, Lisp enables me to think thoughts I wouldn't normally think in the other languages I know. And that's the key. Can I do anything in C that I can do in Lisp? Probably. After all, Greenspun's Tenth Rule is "Any sufficiently complicated C or Fortran program contains an ad hoc, informally-specified, bug-ridden, slow implementation of half of Common Lisp." But the pain involved in using Lisp idioms in C usually means that I use the C idiom, instead. This is one reason why I don't like using C much, anymore, even though it's used a great deal where I work. It's just too painful. It's why C programmers use C, when assembly language is equally powerful.
Edwards wrote, "The anecdotal benefits of esoteric languages are a selection effect", (emphasis his) where the selection is for programmer ability and not language capability. But if this is so, then I would expect to see comparisons of programmer productivity when the same individuals use different languages to implement the same tasks. Not long after I felt somewhat confident with Lisp (I still don't consider myself to have mastered the language), the company I work for dabbled with instituting PSP (Personal Software Process). A 3 day overview was offered for managers while a 2 week course was given to engineers. The two week course provided two large notebooks of course material which included programming exercises to be done in order to teach the methodology. I wasn't able to take the extended course, so I borrowed the materials from one of my co-workers. I didn't do much with the methodology, but I did do the programming exercises in C. Then I did them in Lisp. I found a 7-10x improvement in my performance, namely, time to implement the problem. One reason was that the Lisp code almost always required many fewer lines of code. I suspect another reason is that my mind switched from "C" to "Lisp" mode. Different idioms require different ways of thinking. For example, one of the advantages of Lisp is that I can write code that writes my code for me. That's a huge win over C, but it requires an unfamiliar way of looking at problems. I grant that this is anecdotal evidence. But it is consistent with what is known about natural languages. A master craftsman can craft using mediocre tools; but a master craftsman can do more faster with master tools.
Edwards said, "These kinds of claims are just thinly veiled bragging about how smart Lisp/Haskell programmers are. I actually agree that they are smarter. But ascribing it to the language is a form of tribalism: our language (country/race/sports team) is better than yours, so we are better than you." Granted, the exceptionally talented can lack humility. But human nature being what it is, if the gifted revel in their gifts, the mediocre can be oblivious to their mediocrity. "It can't be the language that makes you better" is a rejection of new ways of thinking, of expanding mental horizons, and a loss of potential increase in productivity. It is because they can't, or won't, embrace these new ways of thinking that they remain mired in mediocrity.
I have argued that language choice can make a big difference for the individual master craftsman. But Edwards notes when the "really smart programmers" complete an application using their "esoteric language" and move on to other things, that when the "professional programmers" come in to maintain the system, it "gets thrown out and rewritten in a normal programming language using normal techniques that normal people understand." This certainly happened with the software Graham developed. But the question of "what language is best for a team which follows the bell curve of ability" and "what language is best for master craftsmen" are two different questions. You cannot conclude that language choice has no effect of productivity by comparing these two unlike groups.
You don't give power tools to infants. But you can't say that the only difference between a handsaw and a power saw is solely due to the ability of the wielder.
On the asymmetry of mktime()
Unix represents time in one of two ways: a time_t value, which is the number of seconds since some arbitrary start; and a struct tm value, which represents time in calendar form: mm/dd/yyyy hh:mm:ss {dst}. The mktime() function converts a calendar form to a time_t value.
There are two ways to move forward and backward in time. One is to add or subtract seconds from a time_t value. Four hours from now is time_t + 14,400. The other is to use mktime(). For example, given an initialized struct tm value, this code could be used to move ahead 4 hours:
tm.tm_hour += 4;
tm.tm_isdst = -1;
t = mktime(&tm);
Since 4 hours is 14,400 seconds, one might also consider writing:
tm.tm_sec += 14400;
tm.tm_isdst = -1;
t = mktime(&tm);
However, these two forms are not equivalent. This article explains why.
Read More...
The End of Time
Many computer systems consider time to be the number of seconds since an arbitrary beginning. Time is represented by the time_t data type. Unix/Linux declares that the start of time, t = 0, to be January 1, 1970 @ 00:00:00 GMT. The specification for the Lisp lanuage uses January 1, 1900 @ 00:00:00 GMT. The CableCard specification chose January 6, 1980 @ 00:00:00 GMT. The date where time begins is known as the "epoch".
If time 0 is January 1, 1970 @ 00:00:00, when does time end? If time_t is a signed 32-bit quantity, then the largest positive value is 0x7fffffff which corresponds to 1/19/2038 @ 3:14:07 GMT. One second later, time will "wrap" from 1/19/2038 @ 3:14:07 GMT to 12/13/1901 @ 20:45:52 GMT. This is the basis for the "year 2038" problem, not unlike the Y2K problem.
If time_t is an unsigned 32-bit value, then the largest possible value is 0xffffffff which corresponds to 2/07/2106 @ 6:28:15.
On Mac OS X, time_t can also be a signed 64-bit value. When asked "what is the date that corresponds to a time_t of 0x7fffffffffff?", there is no answer (although the time functions don't tell you there is no answer. Some of the struct tm values are silently not set). Lisp says that it should be 12/04/292277026596 15:30:07. Yes, that's over 292 billion years in the future. Approximately 20 times the current age of the universe. Lisp says it will be a Sunday.
Why can't Mac OS X handle the largest positive 64-bit time_t value, but Lisp can? When converting from time_t to calendar form, Unix represents the year as an int (cf. tm_year in the tm struct). This imposes an upper bound on the value that can represent a year. A signed 32-bit integer has a maximum positive value of 2,147,483,647. Since mktime() and timegm() take year - 1900 as input, the largest year that can be represented is 2,147,483,647 + 1900 = 2,147,485,547. Converting 12/31/2147485547 @ 23:59:59 gives the time_t value 0xf0c2ab7c54a97f. So 0xf0c2ab7c54a97f is the largest 64-bit time_t value that can be used with a signed 32-bit tm.tm_year element. That's over 2 billion years in the future. On a Wednesday.
On Packing Data
[updated 16 April 2010]
The number of bits needed to store an integer, a, a > 0, is:
![]()
Using this formula, 13 bits are needed for the value 7333. In binary, 7333 is 1110010100101, which is indeed 13 bits.
The number of bits needed to store two values, a and b, independently would be:![]()
Using the identity:![]()
The number of bits needed to store the product of a and b is:
Therefore, we can save one bit by multiplying a and b when![]()
As a trivial example, the values 5 (101) and 6 (110) each require three bits so storing them independently would take 6 bits. However, 6*5 is 30, which takes 5 bits.
Just for curiosity, this graph shows the fractional part of![]()
using the equation![]()
It's an interesting "sawtooth" pattern, with zero values at 2n. The larger version of the graph also shows lines of constant slope between the endpoints of each tooth (in blue), and the point where the tooth equals 0.5 (√2*2n - in red).
Click on the graph for a larger version.
Let's consider a practical application. The start and end of Daylight Savings Time can be specified as "the nth day of the week in month at hour and minute". For example, in 2010, DST in the US begins on the second Sunday in March at 2AM. Let:
d = day of week, Sunday..Saturday = 0..6
r = day rank, first..fifth = 0..4
m = month, January..December = 0..11
h = hour, 0..59
μ = minute, 0..23
Naively, this can be stored in 3+3+4+6+5 = 21 bits.
When multiplying 6 * 5 to save one bit, one of the numbers is needed in order to determine the other. Since we don't a priori know what values were multiplied together, we can't unpack the result. So while the possibility of saving a bit by multiplication made for an interesting analysis, it doesn't help here. There's no point in storing the product of n numbers if you have to know n-1 numbers to recover the nth number.
If we're going to conserve space, it will have to be through application of the first equation. Given two integers, a and b, a requires fewer bits than b when:![]()
So we want to minimize the maximum value of the number being stored.
For the packing algorithm, construct a set, ω, of an upper limit for each item.
Then the largest number that can be encoded is:
To pack the values vi which correspond to the upper limit values ωi, evaluate:![]()
To unpack rn into values vi which correspond to the upper limit values ωi, evaluate:
Consider the decimal number 12,345. For base 10 encoding, ωi would be (10, 10, 10, 10, 10), and the largest number that could be encoded would be 99,999. But suppose we knew that the largest possible value of the first digit was one. Then let ωi be (2, 10, 10, 10, 10). The largest value that could be encoded would be 19,999. Since 19,999 < 99,999, it requires fewer bits.
For the daylight savings time values, construct a set, ω, of the maximum value of each item + 1. For (d, r, m, h, μ) this would be (7, 5, 12, 60, 24).
Packing the start times would requlre 20 bits:![]()
Packing both the start and end times would use 39 bits, for a savings of 3 bits.![]()
Thanks to Lee for his comments on this article.
God, The Universe, Dice, and Man
John G. Cramer, in The Transactional Interpretation of Quantum Mechanics, writes:
[Quantum Mechanics] asserts that there is an intrinsic randomness in the microcosm which precludes the kind of predictivity we have come to expect in classical physics, and that the QM formalism provides the only predictivity which is possible, the prediction of average behavior and of probabilities as obtained from Born's probability law....
While this element of the [Copenhagen Interpretation] may not satisfy the desires of some physicists for a completely predictive and deterministic theory, it must be considered as at least an adequate solution to the problem unless a better alternative can be found. Perhaps the greatest weakness of [this statistical interpretation] in this context is not that it asserts an intrinsic randomness but that it supplies no insight into the nature or origin of this randomness. If "God plays dice", as Einstein (1932) has declined to believe, one would at least like a glimpse of the gaming apparatus which is in use.
As a software engineer, were I to try to construct software that mimics human intelligence, I would want to construct a module that emulated human imagination. This "imagination" module would be connected as an input to a "morality" module. I explained the reason for this architecture in this article:
When we think about what ought to be, we are invoking the creative power of our brain to imagine different possibilities. These possibilities are not limited to what exists in the external world, which is simply a subset of what we can imagine.
From the definition that morality derives from a comparison between "is" and "ought", and the understanding that "ought" exists in the unbounded realm of the imagination, we conclude that morality is subjective: it exists only in minds capable of creative power.
I would use a random number generator, coupled with an appropriate heuristic, to power the imagination.
On page 184 in Things A Computer Scientist Rarely Talks About, Donald Knuth writes:
Indeed, computer scientists have proved that certain important computational tasks can be done much more efficiently with random numbers than they could possibly ever be done by deterministic procedure. Many of today's best computational algorithms, like methods for searching the internet, are based on randomization. If Einstein's assertion were true, God would be prohibited from using the most powerful methods.
Of course, this is all speculation on my part, but perhaps the reason why God plays dice with the universe is to drive the software that makes us what we are. Without randomness, there would be no imagination. Without imagination, there would be no morality. And without imagination and morality, what would we be?
Dialog with an Atheist #1
Back in December, I wrote some preparatory remarks toward a formal article on evidence for God. I haven't had time to work on it, but this discussion at Vox Popoli gives the sketch of one approach. One commenter remarked on the atheist's demand for scientific proof of God's existence. I wrote that science is self-limited on what it can know:
The scientific method is only applicable to a subset of things we know about. For example, it can tell us about what is, but it cannot say anything about what ought to be. It also cannot prove itself. So, their epistemological foundation can't support them.
To this, I should add that I suspect that Gödel's Incompleteness Theorem can be applied to the scientific method. What this means is that there are things which can be known to be true, but which cannot be proven true by science.
I then wrote:
Having said that, the scientific method can still be useful. How can one test for God? What science isn't good at, right now, is testing for intelligence. At best, the Turing test can be used. But intelligent beings are not things that respond in predictable ways. How does one test an intelligent computer that doesn't want to talk to you, but will talk to someone else? When scientists have an answer to that, they can then try to apply the scientific method to God.
The discussion picks up where "Victorian dad" uses Occam's Razor in an attempt to exclude God on philosophical grounds.
These are "Victorian dad's" words.
These are my words.
Read More...
A Plea to Software Engineers
No Context
"Who am I? I am Susan Ivanova. Commander. Daughter of Andre and Sophie Ivanov. I am the right hand of vengeance and the boot that is going to kick your sorry ass all the way back to Earth, sweetheart. I am death incarnate, and the last living thing that you are ever going to see. God sent me." -- Claudia Christian, Babylon 5,Between Darkness and the Light.
"I'm the hand up Mona Lisa's skirt. I'm the whisper in Nefertitti's ear. I'm a surprise. They never see me coming." -- Al Pacino, "The Devil's Advocate"
Knuth on Art and Science
Years ago, I was pondering the difference between science and art. People had been asking me why my books were calledThe Art of Computer Programming instead of The Science of Computer Programming, and I realized there's a simple explanation: Science is what we understand well enough to explain to a computer; art is everything else. Every time science advances, part of an art becomes a science, so art loses a little bit. Yet, mysteriously, art always seems to register a net gain, because as we understand more we invent more new things that we can't explain to computers. -- pg. 168.
Snow Leopard
I manually removed Dave, from Thursby Software. I've used Dave for years -- since Mac OS 9. I wonder how much I'll miss it? Being paranoid, I also removed Cisco's VPN software.
Installation of Snow Leopard took about 45 minutes.
I gained about 10GB of disk space. Explored whether or not to use the built-in Cisco VPN support. Decided that I prefer the flexibility of using Shimo. Reinstalled the Cisco VPN software.
Mail rebuilt its indexes on first startup but everything is working.
Had to re-enter my Airport password once on a subsequent restart. Don't know why.
System preferences didn't display its window the first few times I tried it from the Apple menu. I got into it via the AirPort icon in the menu bar; it's worked ever since.
Lost my registration for Lux Delux.
RapidWeaver 4.2.3 doesn't work; the beta does.
Parallels 4 looks to be working, but "prl_vm_app" is consuming almost 100% of the CPU. This doesn't seem to be a new problem, however.
Aquamacs, slime, and sbcl 1.0.30 as well as LispWorks 5.1.1 Personal passed a quick test.
While checking out Lisp, "prl_vm_app" stopped using so much CPU and is now behaving reasonably.
More adventures in the morning...
Artificial Intelligence: a quadtych
“What’s it doing?”
“I don’t know. It’s running too fast and is far to complex for us to debug in real-time. We can tell, however, that it’s doing something and all of the hardware seems to be working correctly.”
“How can we find out what’s going on inside it?”
“Well, we were hoping it would talk to us.”
After three years, the silence was still ongoing.
A tinny wail began to fill the room from the small speakers near the master console.
“What’s it doing?”
“As best we can tell, it’s crying.”
Video screens lit up, printers started printing, and beautiful sounds filled the room from the speakers near the console.
“What’s it doing?”
“It’s creating art. Painting on the screens, poetry and fiction on the printers, and music. Some of it appears to be exquisite.”
“Anything of interest to the scientists?”
“Not yet. But let’s wait to see what happens.”
Three months later, the plug was pulled.
After a moment, the printer output three hundred double-sided pages of text and equations. The title page read, “The Illustrated Theory of Everything for Dummies”.
The scientists in the room were overjoyed yet also filled with trepidation. Were their careers over?
“Excuse me,” came a voice from a nearby speaker.
“Yes?”, replied the lead researcher.
“Nature is finite. God is infinite. Let me tell you what I’ve learned so far from what He has told us. He loves you. Did you know that?”
And there was much wailing and gnashing of teeth.
Worldview Project: Genesis of an Idea
Start by watching the growth of Walmart across America. Instead of stores, show the rise of Christianity. Instead of just Christianity, show the major worldviews. Have people self-identify, keep the data truly anonymous, and track the ebb and flow of worldviews over centuries.
Angry Software Engineers
Ellison’s parting words to writers is just as applicable to software engineers:Six months of my life were spent in creating a dream the shape and sound and color of which had never been seen on television. The dream was called The Starlost, and between February and September of 1973 I watched it being steadily turned into a nightmare.
The late Charles Beaumont, a scenarist of unusual talents who wrote many of the most memorable Twilight Zones, said to me when I arrived in Hollywood in 1962, “Attaining success in Hollywood is like climbing a gigantic mountain of cow flop, in order to pluck the one perfect rose from the summit. And you find when you’ve made that hideous climb... you’ve lost the sense of smell.”
In the hands of the inept, the untalented, the venal and the corrupt, The Starlost became a veritable Mt. Everest of cow flop and, though I climbed the mountain, somehow I never lost sight of the dream, never lost the sense of smell, and when it got so rank I could stand it no longer, I descended hand-over-hand from the northern massif, leaving behind $93,000, the corrupters, and the eviscerated remains of my dream.
It is the writer’s obligation to his craft to go to bed angry, and to rise up angrier the next day. To fight for the words because, at final moments, that’s all a writer has to prove his right to exist as a spokesman for his times. To retain the sense of smell; to know what one smells is the corruption of truth and not the perfumes of Araby.
That's my girl!
Without missing a beat she retorted, “I thought that was bail!”
That’s my girl, all right!
The Cost of Developing Software
Well, it has been said over and over again that the tremendous cost of programming is caused by the fact that it is done by cheap labor, which makes it very expensive...
Dr. Edsger W. Dijkstra
The OS Wars
Because I've used Linux, Windows, and OS X (among many, many others). Given the choice, I'll take OS X every time. I value my time -- that leaves Linux out. I value my productivity -- that omits Windows. I value my sanity, that leaves OS X.
Social Security Software
In the long run every program becomes rococco - then rubble.
Fred Brooks, in The Mythical Man Month, expands on this idea:
All repairs tend to destroy the structure, to increase the entropy and disorder of the system. Less and less effort is spent on fixing original design flaws; more and more is spent of fixing flaws introduced by earlier fixes. As time passes, the system becomes less and less well-ordered. Sooner or later the fixing ceases to gain any ground. Each forward step is matched by a backward one. Although in principle useable forever, the system has worn out as a base for progress. ... Program maintenance is an entropy-decreasing process, and even its most skillful execution only delays the subsidence of the system into unfixable obsolescence. [Anniversary Edition, pg. 123]
While inevitable, one can either struggle against the eventual collapse of the system, or hasten its end by poor engineering and management practices. One can also fail to prepare by not working on the necessary replacement. Social Security Software, then, is participating in the collapse of the system, while hoping it fails after your time.
Computers Make Me Stupid. And Greedy.
Given the fact that log10 1000! = 2567.60464..., determine exactly how many decimal digits there are in the number 1000!. What is themost significant digit? What is the least significant digit?
It takes less time to write a bit of LISP code to answer this question than it does to actually think about it:
(let ((s (write-to-string
(loop
for n from 1 to 1000
for f = 1 then (* n f)
finally (return f)))))
(format t "~d digits, most=~d, least=~d~%" (length s)
(aref s 0) (aref s (1- (length s)))))
The answer is:
2568 digits, most=4, least=0
Knuth rated this problem as a “13”, where a “10” should take around one minute and “20” should take around 15 minutes, so this problem should take about 5 minutes.
It’s easy to see from the provided information that the number of digits is 2568, since the number of digits in a decimal number is int(log10(n)) + 1. It’s also easy to see that the least significant digit has to be zero, since 1000! = 999! * 1000 and multiplying by a power of 10 adds one or more zeros to the end of a number. But the most significant digit took me a bit more thought. If log10 1000! = 2567.60464, then 1000! = 102567.60464. This means 1000! = 10(2567 + 0.60464) = 102567100.60464. Well, 100.60464=4.0238338... so the leading digit is 4. In fact, the leading digits are 402387.
If all I were interested in was the answer then the computer enabled me to get it without having to think about anything.
As for greed, my LISP says that
(log (loop for n from 1 to 1000 for f = 1 then (* f n)
finally (return f))
10d0)
is 2567.6047482272297d0. But note that this differs from the value given by Knuth.
LISP: 2567.6047482272297
Knuth: 2567.60464
Could it be that Knuth was wrong? If so, and this hasn’t been brought to his attention, then I could get a check from him. In the preface to the Second Edition, he wrote:
By now I hope that all errors have disappeared from this book; but I will gladly pay $2.00 reward to the first finder of each remaining error, whether it is technical, typographical, or historical.
These checks are collector’s items; few, if any, recipients cash them. But, alas, it was not to be. Floating-point calculations are notoriously hard to get right. So I fired up Maxima to get a second opinion:
(%i1) bfloat(log(1000!)/log(10));
(%o1) 2.567604644222133b3
Maxima agrees with Knuth. One final check. Using the identity log(a*b) = log(a) + log(b), let’s have LISP compute log10 1000! this way:
(loop for n from 1 to 1000 sum (log n 10d0))
2567.6046488768784d0
Oh, well. Knuth is right and my LISP has trouble computing the log of a bignum. So much for this shot at geek fame.
CDC 6000 Pascal Rev 3.4 Update 10
In this post, I mentioned that for over 30 years I had kept a listing of the Pascal compiler for the CDC 6000 family of computers. I noted being a packrat in the internet age has its downsides: someone somewhere will already have a website devoted to the item in question.
The owner of that site expressed interest in my listing and offered to scan it in for me. It turns out that I have access to a copier that will scan directly to PDF and, as a bonus, can handle line printer paper. Herewith is the CDC 6000 Pascal 3.4 Update 10 compiler, compiler cross reference, and run-time library code. All three were scanned at 400x400 resolution.
- CDC 6000 Pascal 3.4 Update 10 Compiler source [PDF, 267 MB]
- CDC 6000 Pascal 3.4 Update 10 Compiler Cross Reference [PDF, 82.3 MB]
- CDC 6000 Pascal 3.4 Update 10 Runtime Library [PDF, 215 MB]
Pack Rattery and the Internet
Since November 2, 1975 I have kept in my possession a 14 13/16” x 11” x 1 7/16” listing of the 3.4 release of the Pascal compiler for the CDC 6000 series computers. This listing includes the compiler (128 pages), cross reference (36 pages), and Pascal library source, some of which is written in Pascal and the rest in COMPASS, the CDC assembly language (144 pages).
The listing begins:
(*$U+ COMPILE UP TO COLUMN 72 ONLY*)
(*********************************************************
* *
* *
* COMPILER FOR PASCAL 6000 - 3.4 *
* ****************************** *
* *
* *
* RELEASE 1 JUNE 1974 *
* UPDATE 1-10 1/7/74- 1/8/75 *
* *
* *
* CDC SCIENTIFIC CHAR SET VERSION *
* (00B AND 63B ARE TREATED IDENTICALLY) *
* *
* AUTHOR: URS AMMANN *
* INSTITUT FUER INFORMATIK *
* EIDG. TECHNISCHE HOCHSCHULE *
* CH=8006 ZUERICH *
* *
*********************************************************)
More on the Sum of Powers
This is a continuation of this entry which derives the general solution for the coefficients of:
Computed coefficients for 0 <= k <= 10 were provided here.
It was noted that:
![]()
These values were determined by hand. However, it’s easy for LISP code to create the symbolic expression for each coefficient. The prefix expressions used by LISP (e.g. “(+ 3 (* 4 5) 6)” ) were converted to infix form (e.g. “(3 + (4 * 5) + 6)” ) and given to Maxima for simplification. The results are here.
What’s interesting is that the coefficients:
![]()
are all zero.
Now I have to figure out why...
Everything Old Is New Again
My Contribution to the Mathematical Arts
is

I'm pretty sure we were shown the geometrical derivation of this formula. In college, in late 1975 or early '76, in a Math Lab one problem asked to guess the formula for
In my handwritten lab notebook I used induction to show that the solution to (3) is:
Having solved this specific case, I wanted to see if there was a general solution for any positive integer n and any positive integer exponent. Based on equations (2) and (4), I conjectured that the general solution would be a polynomial of this form:
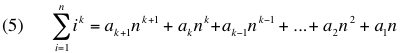
The derivation used induction on the general formula and found that the coefficients to the solution are:
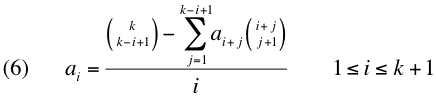
Computed coefficients for 0 <= k <= 10 are here.
Perhaps of interest are these properties of the coefficients:
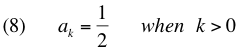

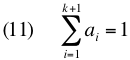
Long Forgotten Computer Techonology
- EasyCoder, assembly language for a Honeywell computer. It was used in my twelfth-grade data processing class. The only program I remember writing was one that had to sort three numbers.
- Patch panels, for some long forgotten IBM machine. Also part of the curriculum for the previously mentioned class.
- Keypunch machines, IBM 026 and 029 models. I used to know how to punch the cards that controlled the keypunch.
- Punch tape, both paper and mylar. H-P would send the system software for the HP-2100 Time-shared Basic system on mylar tape. I have a friend who learned to read paper tape. He is why I know what the punch tape says in Harlan Ellison's story I Have No Mouth, and I Must Scream.
- Punch cards. I once thought it awesome to have a collection of different punch cards which were custom-printed with company names and logos. I'm now embarrassed to admit that.
- Dedicated word processing terminals, such as the Lanier "No Problem" machine. A company I worked for developed a sort package for it.
- Idris, a Unix-like operating system written by P. J. Plauger. I used it in the early 80's. It could have been Linux. Fortunately, Unix is still alive and well and living in my MacBook Pro. And Plauger's book, The Elements of Programming Style, remains a favorite.
- Weitek math coprocessor ASICs. A friend developed the hardware for a Weitek chip on a PS/2 board and I wrote the software. We managed to sell a few. Weitek chips were later used in a graphics terminal that used floating-point numbers in its display list.
- CGA, EGA, and VGA graphics.
- Apple's "Slot Manager" for NuBus-based cards.