Dialog with Jeff Williams: Part IIa
Having set the stage, I will now answer his question:
I would ask you to demonstrate why reason is an atomic arrangement, and why it being a part of nature would imply truth; and along with that how you would explain erroneous ideas and the limits of the invariability principles.
The answer will consist of four parts:
- The road to logic
- The road to truth
- The road to meaning
- The road to math
This post will cover the first topic, the road to logic.
The Road To Logic
Nature provides us with distinguishable objects: electrons, protons, neutrons, six flavors of quarks, positive and negative charge, up and down quantum spin, bumblebees, trees, mushrooms, and more.
Take any two distinguishable objects. For convenience, we use:

We will call these two glyphs "lefty" and "righty" when referring to them in text, since they aren't characters in a font. (I didn't want to use characters from an alphabet, because we associate meaning with characters, and I want to be exquisitely careful to not let meaning creep in from the outside. That I have to refer to these glyphs as "lefty" and "righty" is troublesome enough, but I have to be able to identify them in text.) These characters have unfamiliar shapes and ridiculous names to reinforce the notion that what they are doesn't matter, as long as they are distinguishable. Note that these two glyphs are rotated versions of each other. This isn't strictly necessary, except it makes this presentation easier. What follows would be just as true if beets and bears were used. It's just harder to keep a large supply of beets and bears and swap them out as necessary.
Let us construct a device which has four openings. We will put two openings on the left and one on the right. We will ignore the fourth. The device will be constructed so that two of these glyphs will go into the openings on the left (the "input" ports) and one glyph will come out on the right (the "output" port). The glyph that doesn't come out on the right can be ejected through the fourth opening. We can safely ignore that detail.
With two distinguishable objects, there are four possible combinations at the input ports:
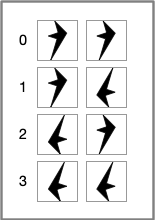
With these four possible combinations on the input port, there are sixteen possible combinations on the output port:
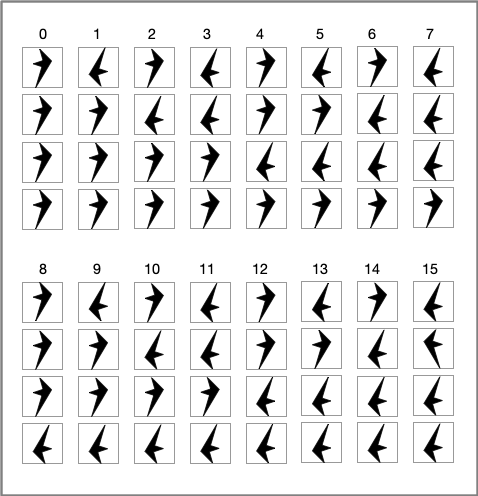
Given input combination three, you might ask how we obtain the fourth row of output combination zero? The output glyph isn't one of the inputs.

That's why an asymmetrical object was chosen. So that we can transform between objects by physical rotation. That's much easier than converting beets into bears.
You may take a pile of two different objects and convince yourself that these are the only possible inputs and outputs. You can cut your work in half by noticing that the output in column 0 is the rotated version of the output in column 15, column 1 to column 14, column 2 to column 13, and so on.
We observe another relationship between the various outputs. Consider a device based on output column 1. It will be represented as a square with two inputs on the left and the output on the right. With this particular device note that the output of column 1 doesn't depend on the order of the input columns. Swapping the input columns results in the same output. This is useful property as we don't have to be concerned about which input goes where.

By chaining this device together we can produce all of the other output combinations
1
: 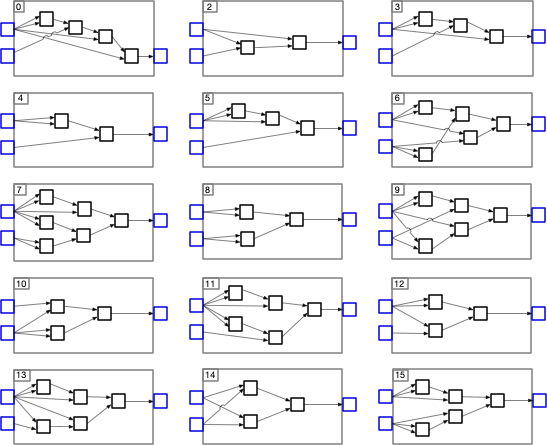
Note that the blue squares are input/output positions.
Because device 1 can produce all of the other possible output combinations, it is called a "universal" combinatorial gate of two objects. Device 7 is also a universal combinatorial gate, but showing this is an exercise for the reader.
Device 1 has another interesting property. In all of the previous examples, device 1 was wired in series with inputs on the left and outputs on the right. Everything flows from left to right with no loops. But suppose we arrange device 1 this way:
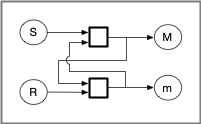
The output of the top device goes both to "M" and the input of the bottom device. The output of the bottom device goes both to "m" and the input of the top device. Suppose the two glyphs are continuously flowing into S and R, and the output continuously appears at M and m. An animation would be ideal to show how this device works, but we'll have to make do with words here.
By design, S and R are initially "lefty," which means M and m are undefined (we won't assume we know what was coming out of the combinatorial devices when input starts flowing. That's an implementation detail.)
Suppose S is set to "righty" before resuming the stream of "lefty". Setting S to "righty" results in M being "lefty" (because "righty" combined with "lefty" or "righty" results in "lefty"). The "lefty" at M is combined with the "lefty" at R which results in "righty" at m. S has now gone back to being "lefty" and combines with the "righty" at "m". The result at M is again "lefty".
This shows that when S is set to "righty," M becomes "lefty" and stays "lefty". m stays "righty".
Suppose R is set to "righty" before reverting back to "lefty". This causes m to become "lefty" (because "righty" as an input always results in "lefty" as output). The "lefty" at m is combined with the input S (which is "lefty") and so M becomes "righty". R has now gone back to being "lefty" and, combined with the "righty" at M results in m being "lefty".
This shows that when R is set to "righty," m becomes "lefty" and stays "lefty". M stays "righty".
The labels M and m were chosen because whatever M is, m is the other glyph. Because M can be set to a desired stream of either glyph, M acts as memory.
Having shown the abilities of a universal combinatorial device, can such a device actually be built? Of course. This particular device is known as a "NAND" gate and is the basis for all modern computers. (The computers on the Apollo spacecraft were built using "NOR" gates, "NOR" being device 7). But these devices can be built in many ways. Some devices use liquid flowing through specially crafted molds. It cannot be stressed enough that how the device is built is irrelevant, as long as it combines two things a certain way. The important thing is the mechanical selection of one object from two. (Later, we'll cover the selection of one object from many. If you want something to do, consider selecting N out of M objects. The complexity grows quickly. You'll need a computer to explore the possibilities. I could have done all of the examples in this post using pen and paper. I didn't, but I could have. Feel free to check my work.)
You now know almost everything you need to know about constructing a device that computes. Yes, important issues were ignored. For example, we assumed that input objects appear at the input ports at the same time. It doesn't matter how this is accomplished. You can build the network of combinatorial devices so that everything happens according to one or more clocks. Or you can build the network so that the length of the paths carrying the objects are of the right length. Or you could combine techniques. We ignored "fan-out," where one output is connected to multiple inputs. We ignored how to push these objects through the combinatorial network. Pushing something requires work and work requires energy. We ignored how to power the network and how to deal with the heat produced by doing the work. We ignored the interface with the world outside the network. This is a critical piece that will be covered later. All of these are important considerations, but these must not become a distraction to the essence of these networks, which is simply the repeated mechanical selection of distinct objects in a network. There is nothing else there.
At this point we have meaningless physical objects running through an arbitrarily arranged network of combinatorial devices. What the network does is purely a function of how the network is arranged. This was demonstrated by the very simple examples of using one combinatorial device to emulate the other 15 devices. Bigger, more complicated networks, will do bigger, more complicated, things. How do we get meaning in such an arrangement? One typical response is "humans put meaning in the network. How humans acquired meaning is a mystery."
Time to take away the mystery in the next part, "The Road To Truth".
[1] These are not the only possible ways to produce the desired results, nor are they guaranteed to be the most efficient. For example, combination 0 could ignore the lower input and use (NAND (NAND x x) x), which would eliminate two gates. Combination 3 could use (NAND x x) and eliminate two gates. Combination 5 could use (NAND y y) (using the bottom input and ignoring the top) and also save two gates. Combinator 12 could wire the top input to the output, and combinator 10 could wire the bottom input to the output eliminating three gates in each.

