Tom
This afternoon my sister informed me that our brother Tom (second of four, two years younger than me) passed away. There are very few additional details at this time.

This picture of Tom with Mom was taken on 12/28/2000. Mom passed on April 16, 2019.
Tom and Scientology: here.
On the Undecidability of Materialism vs. Idealism
According to Douglas Hofstadter1:
What is a self, and how can a self come out of the stuff that is as selfless as a stone or a puddle? What is an "I" and why are such things found (at least so far) only in association with, as poet Russell Edison once wonderfully phrased it, "teetering bulbs of dread and dream" .... The self, such as it is, arises solely because of a special type of swirly, tangled pattern among the meaningless symbols. ... there are still quite a few philosophers, scientists, and so forth who believe that patterns of symbols per se ... never have meaning on their own, but that meaning instead, in some most mysterious manner, springs only from the organic chemistry, or perhaps the quantum mechanics, of processes that take place in carbon-based biological brains. ... I have no patience with this parochial, bio-chauvinist view...
According to the Bible2:
In the beginning was the Word, and the Word was with God, and the Word was God. ... And God said, "Let there be light"; and there was light.
I believe that computability theory, in particular, the lambda calculus, can shed some light on this problem.
In 1936, three distinct formal approaches to computability were proposed: Turing’s Turing machines, Kleene’s recursive function theory (based on Hilbert’s work from 1925) and Church’s λ calculus. Each is well defined in terms of a simple set of primitive operations and a simple set of rules for structuring operations; most important, each has a proof theory.3
All the above approaches have been shown formally to be equivalent to each other and also to generalized von Neumann machines – digital computers. This implies that a result from one system will have equivalent results in equivalent systems and that any system may be used to model any other system. In particular, any results will apply to digital computer languages and any of these systems may be used to describe computer languages. Contrariwise, computer languages may be used to describe and hence implement any of these systems. Church hypothesized that all descriptions of computability are equivalent. While Church’s thesis cannot be proved formally, every subsequent description of computability has been proved to be equivalent to existing descriptions.
It should be without controversy that if a computer can do something then a human can also do the same thing, at least in theory. In practice, the computer may have more effective storage and be much faster in taking steps than a human. I could calculate one million digits of 𝜋, or find the first ten thousand prime numbers, but I have better things to do with my time. It is with controversy that a human can do things that a computer, in theory, cannot do.4 In any case, we don't need to establish this latter equivalence to see something important.
The lambda calculus is typically presented in two parts. Lambda expressions and the lambda expression evaluator:
![]()
One way to understand this is that lambda expressions represent software and the lambda evaluator represents hardware. This is a common view, as our computers (hardware) run programs (software). But this distinction between software and hardware, while economical and convenient, is an arbitrary distinction which hides a deep truth.
Looking first at 𝜆 expressions, they are defined by two kinds of objects. The first set of five arbitrary symbols: 𝜆 . ( ) and space represent simple behaviors. It isn't necessary at this level of detail to fully specify what those behaviors are, but they represent the "swirly, tangled" patterns posited by Hofstadter. The next set of symbols are meaningless. They represent arbitrary objects, called atoms. Here, they are characters are on a screen. They can just as well be actual atoms: hydrogen, oxygen, nitrogen, and so on.
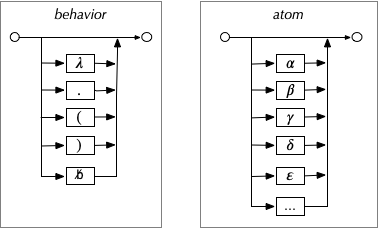
The only requirement for atoms is that they can be "strung together" to make more objects, here called names (naming is hard).

With these components, a lambda expression is defined as:
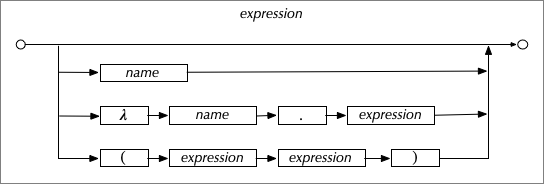
Note that a lambda expression is recursive, that is, a lambda expression can contain a lambda expression which can contain a lambda expression, .... This will become important in a future post when we consider the impact of infinity on worldviews.
With this simple notation, we can write any computer program. Nobody in their right mind would want to, because this notation is so tedious to use. But by careful arrangement of these symbols we can get memory, meaning, truth, programs that play chess, prove theorems, distinguish between cats and dogs.
Given this definition of lambda expressions, and the cursory explanation of the lambda expression evaluator (again, see [3] for details), the first key insight is that the lambda expression evaluator can be written as lambda expressions. Everything is software, description, word. This includes the rules for computation, the rules for physics, and perhaps even the rules for creating the universe.
But the second key insight is that the lambda evaluator can be expressed purely as hardware. Paul Graham shows how to implement a Lisp evaluator (which is based on lambda expressions) in Lisp. And since this evaluator runs on a computer, and computers are logic gates, then lambda expressions are all hardware. With the right wiring, not only can lambda expressions be evaluated, they can be generated. We can (and do) argue about how the wiring in the human brain came to be the way that it is, but that doesn't obscure the fact that the program is the wiring, the wiring is the program. That we can modify our wiring/programming, and therefore our programming/wiring, keeps life interesting.
Therefore, it seems that materialism and idealism remain in a stalemate as to which is more fundamental. It might be that dualism is true, but I think that by considering infinity that dualism can be ruled out as an option, as I hope to show in a future post.
[1] Gödel. Escher, Bach: an Eternal Golden Braid, Twentieth-anniversary Edition; Douglas R. Hofstadter; pg. P-2 & P-3
[2] The Bible, New Revised Standard Version, John 1:1, Genesis 1:3
[3] An Introduction to Functional Programming Through Lambda Calculus, Greg Michaelson
[4] This would require a behavior we cannot observe; a behavior we can't describe; or a behavior we can't duplicate. If we can't observe it, how do we know it's a behavior? A behavior that we can't describe would mean that nature is not self-describing. That seems impossible given the flexibility of description, but who knows?. There might be behaviors we can't duplicate, but that would mean that nature behaves inside human brains like it can behave nowhere else. But there just aren't examples of local violation of general covariance, except by special pleading.
Update 9/30/20
In The Emperor's New Mind, Richard Penrose muses:How can concrete reality become abstract and mathematical? This is perhaps the other side of the coin to the question of how abstract mathematical concepts can achieve an almost concrete reality in Plato’s world. Perhaps, in some sense, the two worlds are actually the same?
Note the unexamined bias. Why not ask, "how can the abstract and mathematical become concrete?" In any case, they can't be the same, since infinity is different in both.

