[updated 16 April 2010]

The number of bits needed to store an integer, a, a > 0, is:

Using this formula, 13 bits are needed for the value 7333. In binary, 7333 is 1110010100101, which is indeed 13 bits.

The number of bits needed to store two values, a and b, independently would be:



Using the identity:



The number of bits needed to store the product of a and b is: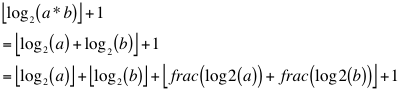



Therefore, we can save one bit by multiplying a and b when



As a trivial example, the values 5 (101) and 6 (110) each require three bits so storing them independently would take 6 bits. However, 6*5 is 30, which takes 5 bits.

Just for curiosity, this graph shows the fractional part of



using the equation



It's an interesting "sawtooth" pattern, with zero values at 2n. The larger version of the graph also shows lines of constant slope between the endpoints of each tooth (in blue), and the point where the tooth equals 0.5 (√2*2n - in red).

Click on the graph for a larger version.



Let's consider a practical application. The start and end of Daylight Savings Time can be specified as "the n^th day of the week in month at hour and minute". For example, in 2010, DST in the US begins on the second Sunday in March at 2AM. Let:

d = day of week, Sunday..Saturday = 0..6
r = day rank, first..fifth = 0..4
m = month, January..December = 0..11
h = hour, 0..59
μ = minute, 0..23

Naively, this can be stored in 3+3+4+6+5 = 21 bits.

When multiplying 6 * 5 to save one bit, one of the numbers is needed in order to determine the other. Since we don't a priori know what values were multiplied together, we can't unpack the result. So while the possibility of saving a bit by multiplication made for an interesting analysis, it doesn't help here. There's no point in storing the product of n numbers if you have to know n-1 numbers to recover the n^th number.

If we're going to conserve space, it will have to be through application of the first equation. Given two integers, a and b, a requires fewer bits than b when:



So we want to minimize the maximum value of the number being stored.

For the packing algorithm, construct a set, ω, of an upper limit for each item.

Then the largest number that can be encoded is: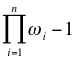

To pack the values v_i which correspond to the upper limit values ω_i, evaluate:



To unpack r_n into values v_i which correspond to the upper limit values ω_i, evaluate: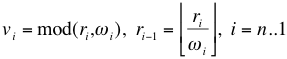



Consider the decimal number 12,345. For base 10 encoding, ω_i would be (10, 10, 10, 10, 10), and the largest number that could be encoded would be 99,999. But suppose we knew that the largest possible value of the first digit was one. Then let ω_i be (2, 10, 10, 10, 10). The largest value that could be encoded would be 19,999. Since 19,999 < 99,999, it requires fewer bits.

For the daylight savings time values, construct a set, ω, of the maximum value of each item + 1. For (d, r, m, h, μ) this would be (7, 5, 12, 60, 24).

Packing the start times would requlre 20 bits:



Packing both the start and end times would use 39 bits, for a savings of 3 bits.



Thanks to Lee for his comments on this article.

[Quantum Mechanics] asserts that there is an intrinsic randomness in the microcosm which precludes the kind of predictivity we have come to expect in classical physics, and that the QM formalism provides the only predictivity which is possible, the prediction of average behavior and of probabilities as obtained from Born's probability law....

While this element of the [Copenhagen Interpretation] may not satisfy the desires of some physicists for a completely predictive and deterministic theory, it must be considered as at least an adequate solution to the problem unless a better alternative can be found. Perhaps the greatest weakness of [this statistical interpretation] in this context is not that it asserts an intrinsic randomness but that it supplies no insight into the nature or origin of this randomness. If "God plays dice", as Einstein (1932) has declined to believe, one would at least like a glimpse of the gaming apparatus which is in use.

When we think about what ought to be, we are invoking the creative power of our brain to imagine different possibilities. These possibilities are not limited to what exists in the external world, which is simply a subset of what we can imagine.

From the definition that morality derives from a comparison between "is" and "ought", and the understanding that "ought" exists in the unbounded realm of the imagination, we conclude that morality is subjective: it exists only in minds capable of creative power.

Indeed, computer scientists have proved that certain important computational tasks can be done much more efficiently with random numbers than they could possibly ever be done by deterministic procedure. Many of today's best computational algorithms, like methods for searching the internet, are based on randomization. If Einstein's assertion were true, God would be prohibited from using the most powerful methods.

Becky, Rachel, and I visited the Wild Animal Safari in Pine Mountain, Georgia. A 3.5 mile road winds through the park; you can ride a bus, rent a van, or drive your car. There is also a walkabout section. We bought a bag of food for each of us and opted for the bus. The animals come right up expecting a treat. We fed buffalo, pigs, deer, and a giraffe. The big cats were caged. Some more pictures and a video of a bear playing with a tire after the fold.

Yesterday I noted the violence in Kyrgyzstan. I visited there in June of '99. I managed to find this picture of Kashka-Suu. Unfortunately, it doesn't do justice to the beauty of the area.

But on the first day of the week, at early dawn, they came to the tomb, taking the spices that they had prepared. They found the stone rolled away from the tomb, but when they went in, they did not find the body. While they were perplexed about this, suddenly two men in dazzling clothes stood beside them. The women were terrified and bowed their faces to the ground, but the men said to them, “Why do you look for the living among the dead? He is not here, but has risen." -- Luke 24:1-5, NRSV