October 2022
Venn Diagrams
[updated 13 October 2023 to include subtraction circuit]
[updated 04 May 2025 to include truth table for add, carry, subtract, and borrow values. Corrected the borrow value to 142 (was 178?!?)]
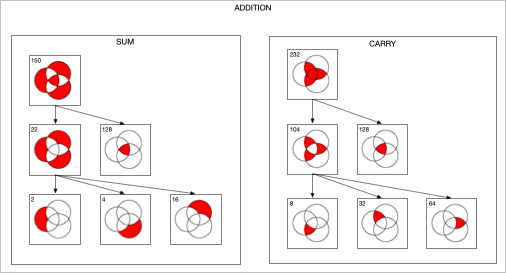
Twelve years ago I played around with designing digital circuits (1, 2, 3) and wrote some code to help in that endeavor. If you can evaluate logical expressions you ought to be able to visualize those expressions. So I extended the code to evaluate logical expressions to generate a Venn diagram of an expression. For review, adders and subtracters have three inputs: the two values to add/subtract and the carry/borrow. The truth tables for these are:
The NAND expressions are:
(NAND Z Z)) (NAND (NAND (NAND (NAND Y Y) (NAND Z X)) (NAND X Y)) Z))
Carry (232): (NAND (NAND (NAND (NAND Y Y) (NAND Z X)) X) (NAND Z Y))
Borrow (142): (NAND (NAND (NAND (NAND X Y) X) Z) (NAND (NAND X Y) Y))
The sum and carry portions of an adder are striking. Click for larger images.
[updated 04 May 2025 to include truth table for add, carry, subtract, and borrow values. Corrected the borrow value to 142 (was 178?!?)]
Twelve years ago I played around with designing digital circuits (1, 2, 3) and wrote some code to help in that endeavor. If you can evaluate logical expressions you ought to be able to visualize those expressions. So I extended the code to evaluate logical expressions to generate a Venn diagram of an expression. For review, adders and subtracters have three inputs: the two values to add/subtract and the carry/borrow. The truth tables for these are:
| x | y | z | add | carry | sub | borrow |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
The NAND expressions are:
Add/Subtract (150):(NAND (NAND (NAND (NAND (NAND X Y) X) (NAND (NAND X Y) Y))
(NAND Z Z)) (NAND (NAND (NAND (NAND Y Y) (NAND Z X)) (NAND X Y)) Z))
Carry (232): (NAND (NAND (NAND (NAND Y Y) (NAND Z X)) X) (NAND Z Y))
Borrow (142): (NAND (NAND (NAND (NAND X Y) X) Z) (NAND (NAND X Y) Y))
The sum and carry portions of an adder are striking. Click for larger images.
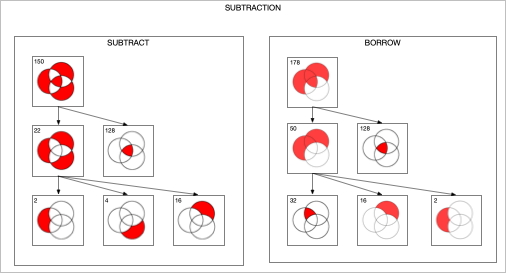
The Venn diagram for the subtraction and borrow equations of a subtraction circuit are similar:
I then produced an animated GIF of all of the 256 Venn diagrams for an equation of 3 variables. The right side is the complement of the equation on the left. 128 images were created, then I used Flying Meat's Retrobatch to resize each image, add the image number, and convert to .GIF format. Then I used the open source gifsicle to produce the final animated .GIF.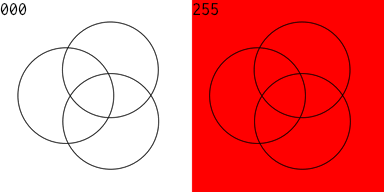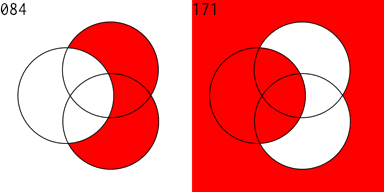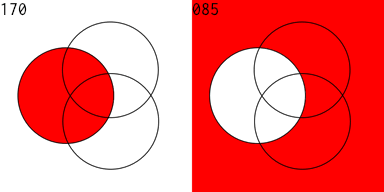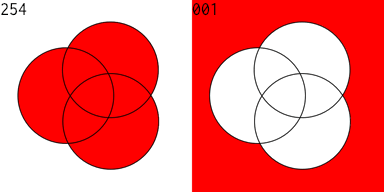
Comments