Two Dialogs on Searle
If a computer can beat you at chess,
it can beat you at philosophy.
The first dialog explores the fundamental mistake Searle makes in his "Chinese Room Argument", namely that while in the general case syntax is insufficient for semantics, programming languages are semantics with syntax. I have written about Searle before (the latest here), but that's me making a case to an empty courtroom. Here, I carry on an adversarial conversation with Grok 3.0 and let it judge the result.
The second dialog considers where Searle can maintain his conclusion that computers cannot be conscious without his "syntax is insufficient for semantics" pillar except by denying the Church-Turing Hypothesis, which he affirms. My position is that he can't, Grok tried to show he can.
Grok is overly verbose, yet sometimes exhibits what appears to be keen insight and sometimes says things in a way that make me jealous that it can be a better wordsmith than me. Grok doesn't get mad, doesn't get frustrated, and doesn't get tired (at least as long as I maintain my $30/month subscription). It is a far more challenging opponent than I typically have access to.
In the future, these discussions will be multi-way with humans and chatbots pushing the boundaries, with the machines keeping everyone honest - demanding definitions, uncovering tacit assumptions, noticing loops, and keeping score. We will be able to save a transcript then ask ChatGPT to read it and comment on it. New insights can be added, repetitious material ignored. The possibility of positive transform is exciting.
Dialog 1 - Searle's mistake
Dialog 2 - Searle and the Church-Turing Hypothesis
Theodicy: Another Perspective

This same change of perspective is possible with the "problem" of evil (and divine hiddenness) which are two arguments employed for the non-existence of [a good] God.
The first step to the change of perspective is to remember that logic does not prove its axioms. It cannot, otherwise one is engaging in circular reasoning. The next step is to recall that logic neither adds to, nor subtracts from, the system described by the axioms. If it isn't "in" the axioms, it doesn't appear as a result; if it is "in" the axioms, it doesn't disappear from the result. Logic is a physical operation, not unlike a meat grinder. Beef in, hamburger out; pork in, ground pork out.
These first two steps should be without controversy. So should the third, but it's less familiar; namely, that nature does not impose on us the axioms that we choose. There are more axioms in "mind" space than there are in "meat" space2,3, and nature does not "tell" us which axioms we should use to describe it.
The switchover may come from the observation that the problem of evil and/or divine hiddenness are problems for some people and not for others. Jesus, for example, affirmed the existence of a good God in Luke 18:19 and denied a problem with hiddenness in his sermon on the mount [Matthew 5:8].
So if evil and hiddenness are problems, then the problem is inherent in the axioms; if they aren't problems, they aren't problems inherent in the axioms.4
Since nature doesn't tell us which axioms to choose, why do we choose the axioms we do? Are these "problems" just a mirror to our souls?
AddendumIt's gratifying to find someone coming to the same conclusion independently. In the coffee shop this morning I read the following and had to update this post.
Our passions infiltrate our intuitions. When in a bad mood, we read someone’s neutral look as a glare; in a good mood, we intuit the same look as interest. Social psychologists have played with the effect of emotions on social intuitions by manipulating the setting in which someone sees a face. Told a pictured man was a Gestapo leader, people will detect cruelty in his unsmiling face. Told he was an anti-Nazi hero, they will see kindness behind his caring eyes. Filmmakers have called this the “Kulechov effect,” after a Russian film director who similarly showed viewers an expressionless man. If first shown a bowl of hot soup, their intuition told them he was pensive. If shown a dead woman, they perceived him as sorrowful. If shown a girl playing, they said he seemed happy. The moral: our intuitions construe reality differently, depending on our assumptions. “We don’t see things as they are,” says the Talmud, “we see things as we are.” – "
Intuition", David G. Myers
[1] I usually make a "v" with my middle and index fingers and look at the dancer through the gap, starting at her feet and moving up until she changes direction. If she doesn't switch by the time I get to the waist, I move down and try again. Sometimes I have to vary with width of the gap. Blink several times and she goes back to the initial direction.
[2] This assumes that there is a difference between the two spaces. We certainly perceive that there is. But, as the dancer illustrates, we might not be looking at reality the right way.
[3] Non-Euclidean geometry is one well-known example of this.
[4] See "The Rules of God Club" for one set of axioms in which evil and hiddenness are not problems.
Bohr on Nature

What's interesting about this is that what Bohr thinks we can say about nature is also what we think we can say about consciousness. We recognize consciousness by behavior (cf. Searle's Chinese Room), but we cannot say whether consciousness is produced by that behavior or whether it is revealed by that behavior.
AGI
If AGI doesn't include insanity as well as intelligence then it may be artificial, but it won't be general.
In "Gödel, Escher, Bach" Hofstadter wrote:
It is an inherent property of intelligence that it can jump out of the task which it is performing, and survey what it is done; it is always looking for, and often finding, patterns.1
Over 400 pages later, he repeats this idea:
This drive to jump out of the system is a pervasive one, and lies behind all progress and art, music, and other human endeavors. It also lies behind such trivial undertakings as the making of radio and television commercials.2
For intelligence to be general, the ability to jump must be in all directions.
[1] Pg. 37
[2] Pg. 478
This idea is repeated in this post from almost 13 years ago. Have I stopped jumping outside the lines?
Quote
1,2
Whether or not the √2 is irrational cannot be shown by measuring it.
Whether or not the Church-Turing hypothesis is true cannot be shown by thinking about it.
[1] "Euclidean and Non-Euclidean Geometries", Greenberg, Marvin J., Second Edition, pg. 7: "The point is that this irrationality of length could never have been discovered by physical measurements, which always include a small experimental margin of error."
[2] This quote is partially inspired by Scott Aaronson's "PHYS771 Lecture 9: Quantum" where he talks about the necessity of experiments.
Searle's Chinese Room: Another Nail
[updated 3/9/2024 - note on Searle's statement that "programs are not machines"]
[updated 10/8/2024;02/09/2025] - added "Searle's Fundamental Error" at beginning to present the gist of why his argument is wrong]
Searle's Fundamental Error
Searle's claim is that because syntax is insufficient for semantics that computers cannot understand meaning the way humans can. What Searle misses is that computer languages are semantics that happen to have syntax. Every computer language is equivalent to a network of logic gates and logic gates specify behavior. These networks can easily implement semantics.Introduction
I have discussed Searle's "Chinese Room Argument" twice before: here and here. It isn't necessary to review them. While both of them argue against Searle's conclusion, they aren't as complete as I think they could be. This is one more attempt to put another nail in the coffin, but the appeal of Searle's argument is so strong - even though it is manifestly wrong - that it may refuse to stay buried. The Addendum explains why.Searle's paper, "Mind, Brains, and Programs" is here. He argues that computers will never be able to understand language the way humans do for these reasons:
- Computers manipulate symbols.
- Symbol manipulation is insufficient for understanding the meaning behind the symbols being manipulated.
- Humans cannot communicate semantics via programming.
- Therefore, computers cannot understand symbols the way humans understand symbols.
- Is certainly true. But Searle's argument ultimately fails because he only considers a subset of the kinds of symbol manipulation a computer (and a human brain) can do.
- Is partially true. This idea is also expressed as "syntax is insufficient for semantics." I remember, from over 50 years ago, when I started taking German in 10th grade. We quickly learned to say "good morning, how are you?" and to respond with "I'm fine. And you?" One morning, our teacher was standing outside the classroom door and asked each student as they entered, the German equivalent of "Good morning," followed by the student's name, "how are you?" Instead of answering from the dialog we had learned, I decided to ad lib, "Ice bin heiss." My teacher turned bright red from the neck up. Bless her heart, she took me aside and said, "No, Wilhem. What you should have said was, 'Es ist mir heiss'. To me it is hot. What you said was that you are experiencing increased libido." I had used a simple symbol substitution, "Ich" for "I", "bin" for "am", and "heiss" for "hot", temperature-wise. But, clearly, I didn't understand what I was saying. Right syntax, wrong semantics. Nevertheless, I do now understand the difference. What Searle fails to establish is how meaningless symbols acquire meaning. So he handicaps the computer. The human has meaning and substitution rules; Searle only allows the computer substitution rules.
- Is completely false.
To understand why 2 is only partially true, we have to understand why 3 is false.
- A Turing-complete machine can simulate any other Turing machine. Two machines are Turing equivalent if each machine can simulate the other.
- The lambda calculus is Turing complete.
- A machine composed of NAND gates (a "computer" in the everyday sense) can be Turing complete.
- A NAND gate (along with a NOR gate) is a "universal" logic gate.
- Memory can also be constructed from NAND gates.
- The equivalence of a NAND-based machine and the lambda calculus is demonstrated by instantiating the lambda calculus on a computer.1
- From 3, every computer program can be written as expressions in the lambda calculus; every computer program can be expressed as an arrangement of logic gates. We could, if we so desired, build a custom physical device for every computer program. But it is massively economically unfeasible to do so.
- Because every computer program has an equivalent arrangement of NAND gates2, a Turing-complete machine can simulate that program.
- NAND gates are building-blocks of behavior. So the syntax of every computer program represents behavior.
- Having established that computer programs communicate behavior, we can easily see what Searle's #2 is only partially true. Symbol substitution is one form of behavior. Semantics is another. Semantics is "this is that" behavior. This is the basic idea behind a dictionary. The brain associates visual, aural, temporal, and other sensory input and this is how we acquire meaning [see "The Problem of Qualia"]. Associating the visual input of a "dog", the sound "dog", the printed word "dog", the feel of a dog's fur, are how we learn what "dog" means. We have massive amounts of data that our brain associates to build meaning. We handicap our machines, first, by not typically giving them the ability to have the same experiences we do. We handicap them, second, by not giving them the vast range of associations that we have. Nevertheless, there are machines that demonstrate that they understand colors, shapes, locations, and words. When told to describe a scene, they can. When requested to "take the red block on the table and place it in the blue bowl on the floor", they can.
I was able to correct my behavior by establishing new associations: temperature and libido with German usage of "heiss". That associative behavior can be communicated to a machine. A machine, sensing a rise in temperature, could then inform an operator of its distress, "Es ist mir heiss!". Likely (at least, for now) lacking libido, it would not say, "Ich bin heiss."
Having shown that Searle's argument is based on a complete misunderstanding of computation, I wish to address selected statements in his paper.
Read More...
The Physical Ground of Logic
[updated 14 January 2024 to add note on semantics and syntax]
[updated 17 January 2024 to add note on universality of NAND and NOR gates]
[updated 26 March 2024 to add note about philosophical considerations of rotation]
The nature of logic is a contested philosophical question. One position is that logic exists independently of the physical realm; another is that it is a fundamental aspect of the physical realm; another is that it is a product of the physical realm. These correspond roughly to the positions of idealism, dualism, and materialism.
Here, the physical basis for logic is demonstrated. This doesn't disprove idealism, dualism, or materialism; but it does make it harder to find a bright line of demarcation between them and a way to make a final determination as to which might correspond to reality.
There are multiple logics. As "zeroth-order" (or "propositional logic") is the basis of all higher logics, we start here.
Begin with two arbitrary distinguishable objects. They can be anything: coins with heads and tails; bees and bears; letters in an alphabet, silicon and carbon atoms. Two unique objects, "lefty" and "righty" are chosen. The main reason is to use objects for which there is no common associated meaning. Meaning must not creep in "the back door" and using unfamiliar objects should help that from inadvertently happening. A secondary engineering reason, with a strong philosophical connection, will be demonstrated later.
| Lefty | Righty |
|---|---|
| \ | | |
These two objects can be combined four ways as shown in the next table. You should be able to convince yourself that these are the only four ways for these combinations to occur. For convenience, each input row and column is labeled for future reference.
| $1 | $2 | |
|---|---|---|
| C0 | \ | \ |
| C1 | \ | | |
| C2 | | | \ |
| C3 | | | | |
Next, observe that there are sixteen ways to select an object from each of the four combinations. You should be able to convince yourself that these are the only ways for these selections to occur. For convenience, the selection columns are labelled for future reference. The selection columns correspond to the combination rows.
| S0 | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | S10 | S11 | S12 | S13 | S14 | S15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C0 | | | | | | | | | | | | | | | | | \ | \ | \ | \ | \ | \ | \ | \ |
| C1 | | | | | | | | | \ | \ | \ | \ | | | | | | | | | \ | \ | \ | \ |
| C2 | | | | | \ | \ | | | | | \ | \ | | | | | \ | \ | | | | | \ | \ |
| C3 | | | \ | | | \ | | | \ | | | \ | | | \ | | | \ | | | \ | | | \ |
Now the task is to build physical devices that combine these two inputs and select an output according to each selection rule. Notice that in twelve of the selection rules it is possible to get an output that was not an input. On the one hand, this is like pulling a rabbit out of a hat. It looks like something is coming out that wasn't going in. On the other hand, it's possible to build a device with a "hidden reservoir" of objects so that the required object is produced. But this is the engineering reason why "lefty" and "righty" are the way they are. "lefty" can be turned into "righty" and "righty" can be turned into "lefty" by rotating the object and rotation is a physical operation on a physical object.
This engineering decision has interesting implications. It ensures that logic is self-contained: what goes in is what comes out. If it doesn't go in, it doesn't come out. The logic gate "not" turns truth into falsity and falsity into truth by a simple rotation. Philosophically, this means that truth and falsity are stance dependent; truth depends on how you look at it. Moving an observer is equivalent to rotating the symbol.
Suppose we can build a device which has the behavior of S7:
We know how to build devices which have the behavior of S7, which is known as a "NAND" (Not AND)1 gate. There are numerous ways to build these devices: with semiconductors that use electricity, with waveguides that use fluids such as air and water, with materials that can flex, neurons in the brain, even marbles.2 NAND gates and NOR gates (S1) are known as universal gates, since arrangements of each gate can produce all of the other selection operations. The demonstration with NAND gates is here. The correspondence between digital logic circuits and propositional logic has been known for a long time.
John Harrison writes3:Digital design Propositional Logic logic gate propositional connective circuit formula input wire atom internal wire subexpression voltage level truth value
The interesting bit now is how to get "truth values" into, or out of, the system. Typically, we put "truth" into the system. We look at the pattern for S7, say, and note that if we arbitrarily declare that "lefty" is "true", then "righty" is false, then we get the logical behavior that is familiar to us. Because digital computers work with low and high voltages, it is more common to arbitrarily make one of them 0 and the other 1 and then to, again arbitrarily, make the convention that one of them (typically 0) represents false and the other (either 1 or non-zero) true.
This way of looking at the system leads to the idea that truth is an emergent behavior in complex systems. Truth is found in the arrangement of the components, not in the components themselves.
But this isn't the only way of looking at the system.
Let us break down the what the internal behavior of each selection process has to accomplish. This behavior will be grouped in order of increasing complexity. To do this, we have to introduce some notation.
~ is the "rotate" operation. ~\ is |; ~| is \.
= tests for equality, e.g. $1 = $2 compares the first input value with the second input value.
? equal-path : unequal-path takes action based on the result of the equal operator.
\ = \ ? | : \ results in |, since \ is equal to \.
\ = | ? | : \ results in \, since \ is not equal to |.
| Selection | Behavior |
|---|---|
| S0 | | |
| S15 | \ |
The second group outputs one of the inputs, perhaps with rotation:
| Selection | Behavior |
|---|---|
| S12 | $1 |
| S3 | ~$1 |
| S10 | $2 |
| S5 | ~$2 |
The third group compares the inputs for equality and produces an output for the equal path and another for the unequal path:
| Selection | Behavior |
|---|---|
| S8 | $1 = $2 ? $1 : | |
| S14 | $1 = $2 ? $1 : \ |
| S1 | $1 = $2 ? ~$1 : | |
| S7 | $1 = $2 ? ~$1 : \ |
| S4 | $1 = $2 ? | : $1 |
| S2 | $1 = $2 ? | : $2 |
| S13 | $1 = $2 ? \ : $1 |
| S11 | $1 = $2 ? \ : $2 |
| S6 | $1 = $2 ? | : \ |
| S9 | $1 = $2 ? \ : | |
It's important to note that whatever the physical layer is doing, if the device performs according to these combination and selection operations then the internal layer is doing these logical operations.
The next step is to figure out how to do the equality operation. We might think to use S9 but this doesn't help. It still requires the arbitrary assignment of "true" to one of the input symbols. The insight comes if we consider the input symbol as an object that already has the desired behavior. Electric charge implements the equality behavior: equal charges repel; unequal charges attract. If the input objects repel then we take the "equal path" and output the required result; if they attract we take the "unequal path" and output that answer.
In this view, "truth" and "falsity" are the behaviors that recognize themselves and disregard "not themselves." And we find that nature provides this behavior of self-identification at a fundamental level. Charge - and its behavior - is not an emergent property in quantum mechanics.
What's interesting is that nature gives us two ways of looking at it and discovering two ways of explaining what we see without, apparently, giving us a clue as to which is the "right" way to look at it. Looking one way, truth is emergent. Looking way, truth is fundamental. Philosophers might not like this view of truth (that truth is the behavior of self-recognition), but our brains can't develop any other notions of truth apart from this "computational truth."
Hiddenness
How the fact that the behavior of electric charge is symmetric, as well as the physical/logical layer distinction, plays into subjective first person experience is here.Syntax and Semantics
In natural languages, it is understood that the syntax of a sentence is not sufficient to understand the semantics of the sentence. We can parse "'Twas brillig, and the slithy toves" but, without additional information, cannot discern its meaning. It is common to try to extend this principle to computation to assert that the syntax of computer languages cannot communicate meaning to a machine. But logic gates have syntax and behavior. The syntax of S7 can take many forms: S7, (NAND x y), NOT AND(a, b); even the diagram of S7, above. The behavior associated with the syntax is: $1 = $2 ? ~$1 : \. So the syntax of a computer language communicates behavior to the machine. As will be shown later, meaning is the behavior of association, this is that. So computer syntax communicates behavior, which can include meaning, to the machine.
More elaboration on how philosophy misunderstands computation is here.
Notes
An earlier derivation of this same result using the Lambda Calculus is here. But this demonstration, while inspired by the Lambda Calculus, doesn't require the heavier framework of the calculus.[1] An "AND" gate has the behavior of S8.
[2] There is a theory in philosophy known as "multiple realizibility" which argues that the ability to implement "mental properties" in multiple ways means that "mental properties" cannot be reduced to physical states. As this post demonstrates, this is clearly false.
[3] "A Survey of Automated Theorem Proving", pg. 27.
Quotes
We know that consciousness and infinity exist "inside" our minds. But we have no
objective way of knowing if they exist "outside" of our minds. There is no objective
measure for consciousness; there is no objective measure for infinity (there are no
rulers of infinite length, or clocks of endless time, for example).
The theist claims that there exists a mind that is both conscious and infinite and
calls this mind God.
The theologian or philosopher who attempts to prove the objective existence of God
is thereby engaging in a futile effort, as is the effort to disprove said existence.
The atheist who asks for objective proof of God is making a category error.
-- wrf3
The Inner Mind
[Similar introductory presentation here]
Philosophy of mind has the problem of "mental privacy" or "the problem of first-person perspective." It's a problem because philosophers can't account for how the first person view of consciousness might be possible. The answer has been known for the last 100 years or so and has a very simple physical explanation. We know how to build a system that has a private first person experience.
Let us use two distinguishable physical objects:

These shapes of these objects are arbitrary and were chosen so as not to represent something that might have meaning due to familiarity. While they have rotational symmetry, this is for convenience for something that is not related to the problem of mental privacy.
Next, let us build a physical device that takes two of these objects as input and selects one for output. Parenthesis will be used to group the inputs and an arrow will terminate with the selected output. The device will operate according to these four rules:

A network of these devices can be built such that the output of one device can be used as input to another device.
It is physically impossible to tell whether this device is acting as a NAND gate or as a NOR gate. We are taught that a NAND gate maps (T T)→F, (T F)→T, (F T)→T, and (F F)→T; (1 1)→0, (1 0)→1, (0 1)→1, (0 0)→0 and that a NOR gate maps (T T)→F, (T F)→F, (F T)→F, (F F)→T; (1 1)→0, (1 0)→0, (0 1)→0, (0 0)→1. But these traditional mappings obscure the fact that the symbols are arbitrary. The only thing that matters is the behavior of the symbols in a device and the network constructed from the devices. Because you cannot tell via external inspection what the device is doing you cannot tell via external inspection what the network of devices is doing. All an external observer sees is the passage of arbitrary objects through a network.1
To further complicate the situation, computation uses the symbol/value distinction: this symbol has that value. But "value" is just elements of the alphabet and so are identical to symbols when viewed externally. That means that to fully understand what a network is doing, you have to discern whether a symbol is being used as a symbol or as a value. But this requires inner knowledge of what the network is doing, which leads to infinite regress. You have to know what the network is doing on the inside to understand what the network is doing from the outside.
Or the network has to tell you what it's doing. NAND and NOR gates are universal logic gates which can be used to construct a "universal" computing device.2
So we can construct a device which can respond to the question "what logic gate was used in your construction?"
Depending on how it was constructed, its response might be:
- "I am made of NAND gates."
- "I am made of NOR gates."
- "I am made of NAND and NOR gates. My designer wasn't consistent throughout."
- "I don't know."
- "What's a logic gate?"
- "For the answer, deposit 500 bitcoin in my wallet."
Before the output device is connected to the system so that the answer can be communicated, there is no way for an external observer to know what the answer will be.
All an external observer has to go on is what the device communicates to that observer, whether by speech or some other behavior.3
And even when the output device is active and the observer receives the message, the observer cannot tell whether the answer given corresponds to how the system was actually constructed.
So extrospection cannot reveal what is happening "inside" the circuit. But note that introspection cannot reveal what is happening "outside" the circuit. The observer doesn't know what the circuit is doing; the subject doesn't know how it was built. It may think it does, but it has no way to tell.
[1] Technology has advanced to the point where brain signals can be interpreted by machine, e.g. here. But this is because these machines are trained by matching a person's speech to the corresponding brain signals. Without this training step, the device wouldn't work. Because our brains are similar, it's likely possible that a speaking person could train such a machine for a non-vocal person.
[2] I put universal in quotes because a universal Turing machine requires infinite memory and this would require an infinite number of gates. Our brains don't have an infinite number of neurons.
[3] See also Quss, Redux, since this has direct bearing on yet another problem that confounds philosophers, but not engineers.
On the Knowledge of God
[updated 11/21/2020 to change "all side" to "all sides"]
[updated 7/20/2022 to add quotes from Markides and Oppy]
I'm just this guy, you know?1 One of the possible recent mistakes I have made is getting involved with Twitter, in particular, with some of the apologists for theism and for atheism whose goal is to prove by reason that God does, or does not, exist. Over time, having examined both the arguments both for and against, I have come to the conclusion that neither side has any arguments that aren't in some way fundamentally flawed. One day, I will make this case in writing (I still have much more preparation to do first). Still, the failure of one argument doesn't automatically prove the opposite case. So the failure of the arguments on all sides does not mean that a good argument doesn't exist. It just means we haven't found it. Yet, once you see the structure of these arguments, their commonalities, and the problems with them, you begin to wonder if it isn't a hopeless enterprise in the first place. Hence my proposed "Spock-Stoddard Test" and "The Zeroth Commandment." To be sure, these are not based on rigorous proof, but merely on informed guesswork. But they encapsulate the notion that whether or not one believes or disbelieves in God is a logically free choice. It is primal. It is not entailed by other considerations. You either do, or you don't, for no other reason that you do, or you don't. Post-hoc rationalizations don't count.
When one is, as it were, the "lone voice crying in the desert" with an opinion that appears to be relatively rare, at least in the circles I run in, it's gratifying to find others who have come to the same conclusion. Clearly, group cohesion doesn't make my position true or false, but it does make it less lonely. Herewith are a few quotes that I've come across along the way.
He is not in the business of giving them arguments that will prove he has some derivative right to their attention; he is only inviting them to believe. This is the hard stone in the gracious peach of his Good News: salvation is not by works, be they physical, intellectual, moral, or spiritual; it is strictly by faith in him. ... Jesus obviously does not answer many questions from you or me. Which is why apologetics-the branch of theology that seeks to argue for the justifiability of God's words and deeds-is always such a questionable enterprise. Jesus just doesn't argue. ... He does not reach out to convince us; he simply stands there in all the attracting/repelling fullness of hisexousia and dares us to believe. -- Robert Farrar Capon. Parables of Judgment
Jesus did not, indeed, support His theism by argument; He did not provide in advance answers to the Kantian attack upon the theistic proofs. -- J. Gresham Machen,Christianity and Liberalism
Like probably nothing else, all authentic knowledge of God is participatory knowledge. I must say this directly and clearly because it is a very different way of knowing reality—and it should be the unique, open-horizoned gift of people of faith. But we ourselves have almost entirely lost this way of knowing, ever since the food fights of the Reformation and the rationalism of the Enlightenment, leading to fundamentalism on the Right and atheism or agnosticism on the Left. Neither of these know how to know! We have sacrificed our unique telescope for a very inadequate microscope.The Divine Dance
...
In other words, God (and uniquely the Trinity) cannot be known as we know any other object—such as a machine, an objective idea, or a tree—which we are able to “objectify.” We look at objects, and we judge them from a distance through our normal intelligence, parsing out their varying parts, separating this from that, presuming that to understand the parts is always to be able to understand the whole. But divine things can never be objectified in this way; they can only be “subjectified” by becoming one with them! When neither yourself nor the other is treated as a mere object, but both rest in an I-Thou of mutual admiration, you have spiritual knowing. Some of us call this contemplative knowing. -- Richard Rohr,
Reformed theology regards the existence of God as an entirely reasonable assumption, it does not claim the ability to demonstrate this by rational argumentation. Dr. Kuyper speaks as follows of the attempt to do this: “The attempt to prove God’s existence is either useless or unsuccessful. -- Louis Berkhof,Systematic Theology
Today, it is generally agreed that there can be no logical proof either way for the existence of God, and that this is purely a matter of faith. -- Marcus Weeks,Philosophy in Minutes
But the way to know God, Father Maximos would say repeatedly, is neither through philosophy nor through experimental science but through systematic methods of spiritual practice that could open us up to the Grace of the Holy Spirit. Only then can we have a taste of the Divine, a firsthand, experiential knowledge of the Creator. -- Kyriacos C. Markides,The Mountain of Silence
I think that such theists and atheists are mistaken. While they may be entirely within their rights to suppose that the arguments that they defend aresound, I do not think that they have any reason to suppose that their arguments are rationally compelling... -- Graham Oppy, Arguing About Gods
One final quote is appropriate:
Blessed are the pure in heart, for they will see God. -- Matthew 5:8, NRSV
[1] Said of Zaphod Beeblebrox, "The Restaurant and the End of the Universe"
Evidence for Christianity
At some point, it pays to stop beating your head against a wall and see if a fresh approach doesn't yield a new way to look at the problem.
The theory of computation shows that computation is certain behaviors on meaningless symbols (cf. the Lambda Calculus). We know, from the Lambda Calculus, how to derive logic. Once we have logic, we can derive meaning. From there, we can derive math, morality, and everything else for a human level intelligence. One can replace the meaningless symbols with physical atoms and show how neurons implement computation. And we know from computability theory, that how the device is implemented isn't what's important - it's the behavior.
We know that human level sentient creatures have a sense of self. It is something we are directly aware of, but outside observers cannot measure it objectively. Our thoughts, our ego, are "inside" the swirling atoms in our brains. An outside observer can only see the behavior caused by the swirl of atoms. Certainly, we can hook electrodes up to brains and measure electrical activity. But we cannot know what that activity corresponds to internally, unless the test subject tells us. It is only because we share common brain structures that we can try to predict which activity has what meaning in others.
The swirl of atoms in our brains, the repeated combination and selection of meaningless symbols, is a microcosm of the swirling of atoms in the universe. If our brains are localized intelligence, the case can be made that swirl of atoms in the universe is a global intelligence. But this is a subjective argument. This is why the Turing Test is conducted where an observer cannot see the subject. Seeing the human form biases us to conclude human intelligence. But for a non-human form, an observer has to recognize sentience from behavior. Why might that not be the case?
First, because there is a lot of randomness in the behavior of the universe and it is a common idea that randomness is ateleological. It lacks meaning and purpose. Unfortunately, this philosophical stance is without merit, since randomness can be used to achieve determined ends. The fact of randomness simply isn't enough to move the needle between purpose/purposelessness and meaning/meaninglessness. One could argue that human intelligence contains a great deal of randomness. But an observer looking on the outside cannot objectively see which is the case.
Second, because the behavior of the universe doesn't always comport with our desires. Our standards of good and evil are not the universe's standards of good and evil. If one holds to an objective morality, one will miss the possible sentience of someone who behaves very differently from ourselves.
Third, we want to think that there is only one objectively right way to view the universe. But the universe doesn't make that easy. We have the built-in knowledge of infinity (an endless and therefore unmeasurable process). There is no consensus whether infinity is "real" or "actual" and, since we can't measure it, I don't think consensus will ever be achieved. There is also the question of whether matter produces and moves the mind or mind produces and moves matter. Neither side has achieved consensus.
Into this mix comes Christianity which states that there is an extra-human intelligence "inside" the existence and motion of the universe, who has a sense of right and wrong that is different from ours, where what has been made is a strong indication of that sentience, and who calls people to itself. Because sentience is a subjective measurement, it must be made on faith - which is one of the bedrock tenets of Christianity. This picture of local intelligences inside a bigger intelligence is consistent with "in Him we live and move and have our being." Yet in spite of this connectedness, we remain disconnected, not recognizing our state. Which is yet another teaching of Christianity.
Much more can, and must, be said. But the immateriality and incommensurability of infinity; the subjectivity of sentience and morality; and the ability to build thinking things out of dirt are all a part of both Christianity and natural theology.
Quus, Redux
Philip Goff explores Kripke's quss function, defined as:
In English, if the two inputs are both less than 100, the inputs are added, otherwise the result is 5.
(defparameter N 100)
(defun quss (a b)
(if (and (< a N) (< b N))
(+ a b)
5))
Goff then claims:
Rather, it’s indeterminate whether it’s adding orquadding.
This statement rests on some unstated assumptions. The calculator is a finite state machine. For simplicity, suppose the calculator has 10 digits, a function key (labelled "?" for mystery function) and "=" for result. There is a three character screen, so that any three digit numbers can be "quadded". The calculator can then produce 1000x1000 different results. A larger finite state machine can query the calculator for all one million possible inputs then collect and analyze the results. Given the definition of quss, the analyzer can then feed all one million possible inputs to quss, and show that the output of quss matches the output of the calculator.
Goff then tries to extend this result by making N larger than what the calculator can "handle". But this attempt fails, because if the calculator cannot handle bigN, then the conditionals (< a bigN) and (< b bigN) cannot be expressed, so the calculator can't implement quss on bigN. Since the function cannot even be implemented with bigN, it's pointless to ask what it's doing. Questions can only be asked about what the actual implementation is doing; not what an imagined unimplementable implementation is doing.
Goff then tries to apply this to brains and this is where the sleight of hand occurs. The supposed dichotomy between brains and calculators is that brains can know they are adding or quadding with numbers that are too big for the brain to handle. Therefore, brains are not calculators.
The sleight of hand is that our brains can work with the descriptions of the behavior, while most calculators are built with only the behavior. With calculators, and much software, the descriptions are stripped away so that only the behavior remains. But there exists software that works with descriptions to generate behavior. This technique is known as "symbolic computation". Programs such as Maxima, Mathematica, and Maple can know that they are adding or quadding because they can work from the symbolic description of the behavior. Like humans, they deal with short descriptions of large things1. We can't write out all of the digits in the number 10^120. But because we can manipulate short descriptions of big things, we can answer what quss would do if bigN were 10^80. 10^80 is less than 10^120, so quss would return 5. Symbolic computation would give the same answer. But if we tried to do that with the actual numbers, we couldn't. When the thing described doesn't fit, it can't be worked on. Or, if the attempt is made, the old programming adage, Garbage In - Garbage Out, applies to humans and machines alike.
[1] We deal with infinity via short descriptions, e.g. "10 goto 10". We don't actually try to evaluate this, because we know we would get stuck if we did. We tag it "don't evaluate". If we actually need a result with these kinds of objects, we get rid of the infinity by various finite techniques.
[2] This post title refers to a prior brief mention of quss here. In that post, it suggested looking at the wiring of a device to determine what it does. In this post, we look at the behavior of the device across all of its inputs to determine what it does. But we only do that because we don't embed a rich description of each behavior in most devices. If we did, we could simply ask the device what it is doing. Then, just as with people, we'd have to correlate their behavior with their description of their behavior to see if they are acting as advertised.
Truth, Redux
Logic is mechanical operations on distinct objects. At it simplest, logic is the selection of one object from a set of two (see "The road to logic", or "Boolean Logic"). Consider the logic operation "equivalence". If the two input objects are the same, the output is the first symbol in the 0th row ("lefty"). If the two input objects are different, the output is the first symbol in the 3rd row ("righty").
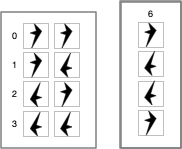
If this were a class in logic, the meaningless symbols "lefty" and "righty" would be replaced by "true" and "false".
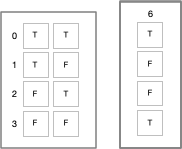
But we can't do this. Yet. We have to show how to go from the meaningless symbols "lefty" and "righty" to the meaningful symbols "T" and "F". The lambda calculus shows us how. The lambda calculus describes a universal computing device using an alphabet of meaningless symbols and a set of symbols that describe behaviors. And this is just what we need, because we live in a universe where atoms do things. "T" and "F" need to be symbols that stand for behaviors.
We look at these symbols, we recognize that they are distinct, and we see how to combine them in ways that make sense to our intuitions. But we don't know we do it. And that's because we're "outside" these systems of symbols looking in.
Put yourself inside the system and ask, "what behaviors are needed to produce these results?" For this particular logic operation, the behavior is "if the other symbol is me, output T, otherwise output F". So you need a behavior where a symbol can positively recognize itself and negatively recognize the other symbol. Note that the behavior of T is symmetric with F. "T positively recognizes T and negatively recognizes F. F positively recognizes F and negatively recognizes T." You could swap T and F in the output column if desired. But once this arbitrary choice is made, it fixes the behavior of the other 15 logic combinations.
In addition, the lambda calculus defines true and false as behaviors.1 It just does it at a higher level of abstraction which obscures the lower level.
In any case, nature gives us this behavior of recognition with electric charge. And with this ability to distinguish between two distinct things, we can construct systems that can reason.
[1] Electric Charge, Truth, and Self-Awareness. This was an earlier attempt to say what this post says. YMMV.
On Rasmussen's "Against non-reductive physicalism"
It should be without controversy that there are more non-physical things than physical things. By some estimates there are 10^80 atoms in the universe. There are an unlimited number of numbers. We can't measure all of those numbers, since we can't put them in one-to-one correspondence with the "stuff" of the universe.
The first thing to note is that if the number of things argues against the physicality of mental states, then mental properties aren't needed, because there are more atoms in the universe than there are in the brain. If the sheer number of things argues against physical mental states then this would be sufficient to prove the claim. But as anyone who plays the piano knows, 88 keys can produce a conceptually infinite amount of music. And one need not postulate non-physicality to do so. Just hook a piano up to random number sources that vary the notes, tempo, and volume. The resulting music may not be melodious, but it will be unique.
Rasmussen presents a "construction principle" which states "for any properties, the xs, there is a mental property of thinking that the xs are physical." Here the confusion between mental property and mental state happens. The argument sneaks in the desired conclusion. After all, if this principle were true, then the counting argument wouldn't be needed. Clearly, there is a mental state when I think "my HomePod is playing Cat Stevens". But whether that mental state is physical or immaterial is what has to be shown. By saying it's a mental property then the assertion is mental states are non-physical and the rest of the proof isn't necessary. It's just proof by assertion.
Rasmussen then gives what he calls "a principle of uniformity" which says, "The divide between any two mental properties is narrower than the divide between physicality and non-physicality." To demonstrate this difference between physical and non-physical, he gives the example of a tower of Lego blocks. His claim is that as Lego block is stacked on Lego block, that both the Lego tower, and the shape of the Lego tower, remains physical. He asserts, "if (say) being a stack of n Lego blocks is a physical property, then clearly so is being a stack of n+1 Lego blocks, for any n." This is clearly false. A Lego tower of 10^90 pieces is non-physical. There aren't enough physical particles in the universe for constructing such a tower. Does the shape of the Lego tower remain physical? This is a more interesting question. A shape is a description of an arrangement of stuff. The shape of an imaginary rectangle and the shape of a physical rectangle are the same. Are descriptions physical or non-physical? To assert one or the other is to beg the question of the nature of mental states.
So we have a counting argument that isn't needed, a construction principle that begs the question, and a principle of uniformity that doesn't match experience.
Having failed to show that mental states are non-physical, in section 3 Rasmussen tries to show that mental states aren't grounded in physicality. The bulk of the proof is in his step B2: "if no member of MPROPERTIES entails any other, then some mental properties lack a physical grounding." He turns the counting argument around to claim that there is a problem of too few physical grounds for mental states. This claim is easily dismissed. First, consider words. The estimated vocabulary of an average adult speaker of English is 35,000 words. There is plenty of storage in the human brain for this. But if we don't know a word, we go to the dictionary to get a new definition and place that definition in short term reusable storage. If we use it enough so that it goes into long term storage, we may forget something to make room for it.
In the case of "infinite" things, we think of them in terms of a short fixed description of behavior, so we don't need a lot of storage for infinite things. The computer statement
is a short description of an endless process. We don't actually think of the entire infinite thing, but rather finite descriptions of the behavior behind the process. [1]
10 goto 10
Rasmussen's proof fails because the claim that there needs to be a unique physical property for each mental state doesn't stand. Much of our physical memory is reusable and we have access to external storage (books, videos, other people). In fact, as I wrote in 2015, "man is the animal that uses external storage". [2]
Since the final sections 4 and 5 aren't supported by 1, 2, and 3, they will be skipped over.
[1] See "Lazy Evaluation" for some ways to deal with infinite sequences with limited storage.
[2] "Man is the Animal...". Almost seven years later, this statement is still unique to me. Don't know why. It's obvious "to the most casual observer."
The End of Philosophy
While Russell was working on his Principa, Kurt Gödel's Incompleteness Theorems came along and proved that a self-describing system (i.e. a system that is sufficiently complex to express the basic arithmetic of the natural numbers) cannot simultaneously be consistent and complete. If it's consistent, it's not complete; if it's complete, it isn't consistent.
This ended Russell's lifelong dream. While his Principa is a tremendous intellectual achievement, it did not - and could not - achieve the goals Russell had for his work.
If nature is self-describing (as I think the posts on Natural Theology will show, once they're organized and edited for clarity), then philosophy suffers the same problem as mathematics. Empirically, the universe appears to be consistent. If we put a stake in that position, then all descriptions of nature will be incomplete. There will be no final "theory of everything."
If that's so then, observationally, there are questions for which we cannot know the answers. One such question is on the ontological nature of endlessness (infinity). Is endlessness emergent from a finite universe, or is the universe infinite and what we perceive as reality a quantization of this continuity? It's interesting that the theory of relativity is based on an infinitely continuous picture of nature. Quantum mechanics is based on a discrete picture of nature. String theory tries to split the difference by postulating tiny vibrating strings, but if nature has continuous/discontinuous duality like matter has wave/particle duality, then string theory may, like Russell's Principa, fall short of its intended goal.
Another such question is the nature of randomness. Does randomness indicate purposelessness (as the naturalists claim) or does it indicate hidden purpose (as the theists claim)? The value of 𝜋 can be computed by a deterministic formula. It can also be calculated via Monte Carlo methods (see Buffon's Needle). Therefore, the use of randomness does not preclude agency. Nor does it establish it.
Given that these questions cannot be answered, I propose "Newton's" Third Law of Metaphysics: there are some fundamental questions for which for every answer there is an equal and opposite answer. A corollary to this is that the question of the existence/non-existence of God is in this class. Certainly, the inability over thousands of years of arguing to establish a decisive conclusion is evidence of this principle. Or it may be that the right insight hasn't yet been achieved. An answer which is also evidence of this principle.
I think Gödel has done to philosophy what he did to math. Philosophy won't end, since math didn't end. But it will put limits on what philosophy can say about certain things. I said as much in the post "Epistemology and Hitchens" but that was before I think that the idea that nature is self-describing could be demonstrated from the ground up.
On Self
While I agree with this sentiment (after all, Psalm 57:1 says that God has wings), Dr. Tuggy has also used this idea to defend Unitarianism. More specifically, Dr. Tuggy lists 20 self-evident principles that he uses to guide his reading of Scripture.
While this post is not meant to focus on the debate between Trinitarians and Unitarians, I do want to use Dr. Tuggy's tweet as a springboard to consider if his "self-evident" truths are universally self-evident. I think there is reason to believe that they may not be.
Not long after we are born, we start to distinguish ourselves from our surroundings. We can feel a difference between ourselves and our environment. Place your hand on a table and run your finger from your hand to the table and notice the boundary your senses tell you is there. Look at your hand and notice the boundary between your hand and the table. Lift your hand from the table and notice that your hand moves but the table does not. Look in a mirror and notice the difference between you and your environment. All of these sense data tells us that we are distinct self-contained objects.
But our senses also tell us that the table on which our hand rests is solid. In reality, the table is mostly empty space. What we perceive as solidness is the repulsion of the electric field from the electrons in the table against the like-charged electrons in our hand. If we perceive a location for ourselves, we generally place it inside our skulls. To nature, there is no inside. Billions of neutrinos pass through a square centimeter every second. The experimental particle physicist, Tommaso Dorigo, speculates:
... a few energetic muons are crossing your brain every second, possibly activating some of your neurons by the released energy. Is that a source of apparently untriggered thoughts? Maybe.
4gravitons writes:
This is Quantum Field Theory, the universe of ripples. Democritus said that in truth there are only atoms and the void, but he was wrong. There are no atoms. There is only the void. It ripples and shimmers, and each of us lives as a collection of whirlpools, skimming the surface, seeming concrete and real and vital…until the ripples dissolve, and a new pattern comes.
From a physical view, what we are, are ripples in the quantum pond, with our "selves" limited to local interaction by an inverse square law. From a Biblical view,
‘In him we live and move and have our being’
— Acts 17:28, NRSV
I suspect there is no "inverse square law" with spirit so what separates us from one another is a... mystery.1
[1] Almost immediately after hitting "publish", I started kicking myself. Scripture says what separates us, from God and from each other:
Rather, your iniquities have been barriers between you and your God ...
— Isa. 59:2, NRSV
Ought From Is
To get "ought" from "is", take an "is" and move it into the future as a goal.
The Universe Inside
Let us replace distinguishable objects with objects that distinguish themselves:
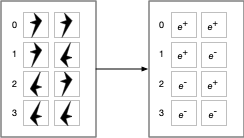
Then the physical operation that determines if two elements are equal is:

As shown in the previous post, e+ (the positron and its behavior) and e- (the electron and its behavior) are the behaviors assigned to the labels "true" and "false". One could swap e+ and e-. The physical system would still exhibit consistent logical behavior. In any case, this physical operation answers the question "are we the same?", "Is this me?", because these fundamental particles are self-identifying.
From this we see that logical behavior - the selection of one item from a set of two - is fully determined behavior.
In contrast to logic, nature features fully undetermined behavior where a selection is made from a group at random. The double-slit experiment shows the random behavior of light as it travels through a barrier with two slits and lands somewhere on a detector.
In between these two options, there is partially determined, or goal directed behavior where selections are made from a set of choices that lead to a desired state. It is a mixture of determined and undetermined behavior. This is where the problem of teleology comes in. To us, moving toward a goal state indicates purpose. But what if the goal is chosen at random? Another complication is that, while random events are unpredictable, sequences of random events have predictable behavior. Over time, a sequence of random events with tend to its expected value. We are faced with having to decide if randomness indicates no purpose or hidden purpose, agency or no agency.
In this post, from 2012, I made a claim about a relationship between software and hardware. In the post, "On the Undecidability of Materialism vs. Idealism", I presented an argument using the Lambda Calculus to show how software and hardware are so entwined that you can't physically take them apart. This low-level view of nature reinforces these ideas. All logical operations are physical (all software is hardware). Not all physical operations are logical (not all hardware is software). Computing is behavior and the behavior of the elementary particles cannot be separated from the particles themselves. If we're going to choose between idealism and physicalism, it must be based on a coin flip2.
If computers are built of logic "circuits" then computer behavior ought to be fully determined. But when we add peripherals to the system and inject random behavior (either in the program itself, or from external sources), we get non-logical behavior in addition to logic. If a computer is a microcosm of the brain, the brain is a microcosm of the universe.
[1] Quarks have fractional charge, but quarks aren't found outside the atomic nucleus. The strong nuclear force keeps them together. Electrons and positrons are elementary particles.
[2] Dualism might be the only remaining choice, but I think that dualism can't be right. That's a post for another day.
Electric Charge, Truth, and Self-Awareness
John 18:38, NRSV
What is truth?
— Pilate,
To say of what is that it is not, or of what is not that it is, is false, while to say of
what is that it is, and of what is not that it is not, is true.
— Aristotle
"The truth points to itself."
"What?"
"The truth points to itself."
"I do not understand."
"You will."
— Kosh and Delenn in Babylon 5:"In the Beginning"
The one quote that I want, but can no longer find, is to the effect that philosophers don't really know what truth is. Introductions to the philosophy of truth (e.g. here) make for fascinating reading. I claim that the philosophers can't reach agreement because they aren't trying to build a self-aware creature. Were they to attempt it, they might reason something like the following.
Aristotle's definition of truth is clumsy. It simplifies to:If true then [say] true is true.
In hindsight, this isn't a totally terrible definition. It combines the behavior (say "true") with the behavior ("truth leads to truth"). But it's still circular. "True ... is true" doesn't tell us what truth is, so it's useless for building something.
Still, this formulation anticipated a definition of truth in computer programming languages by some 1,700 years:if true then truth-action else false-action
"True" is a special symbol that is given the special meaning of truth. In Lisp, t is true and nil is false. In FORTRAN, .true. is true and .false. is false. Python uses True and False. And so on. But this still doesn't tell you what truth is other than it is a special symbol that can be used for making selections.
Looking at how "true" is defined in the Lambda Calculus provides a critical clue. Considering the Lambda Calculus is important, because it describes all computation in terms of behaviors (denoted by the special symbols λ, ., (, ), and blank) and meaningless symbols. There is no special symbol for "true".def true = λx.λy.x
What this means is that "true" is a function of two objects, x and y and it returns the first object x. Truth is a behavior that can be used as a property. That is, this behavior can be attached to other symbols. It is the behavior that selects true things and rejects false things. False has symmetric behavior. It selects false things and rejects true things. So we've advanced from a special symbol to a behavior. But we aren't yet done.
The simplest if-then statement is:if true then true else false
Truth is the behavior that selects itself. So we've derived the basis for the quote from Babylon 5, above. But we need to take one more step. Fundamental to the Lambda Calculus is the ability to distinguish between symbols. It is a behavior that is assumed by the Lambda calculus, one that doesn't have a special symbol like λ, ., (, ), and space to denote the behavior of distinguishing between symbols.
So consider a Lambda Calculus with two symbols:
And so, we find that truth is the ability to recognize self and select similar self-recognizing things.
And so, we find that electric charge gives us the laws of thought and truth, all in one force.
On Formal Proofs For/Against God
[Updated 2/2/2024]
Over on Ed Feser's blog, is another attempt, in a never-ending series of attempts, to formally prove the existence of God. [1] I was playing devil's advocate by taking the position that the answer to Feser's question is a resounding "no" by providing counter-arguments to their arguments. [2] [3]
"Talmid" made the statement:
You can defend that the arguments fail...
This is where the light came on.
Nobody would say of the proof of the Pythagorean theorem, or of the non-existence of a largest prime number, that "the arguments fail." That isn't how proofs work. If a proof fails, it's because of one of two reasons. Either a premise is denied, or there is a mistake in the mechanical procedure of constructing the proof. When you read these proofs of God's existence (or non-existence), at some point you come to a step in the proof where it looks like the next logical step was taken by coin-flip, instead of logical necessity. This is evidence of the presence of an unstated premise.
Find the unstated premises. Don't let your common sense get in the way. [4] If the argument assumes that things have a beginning, question it. Why must history be linear and not, say, circular? [5] Why can't something come from nothing? That may defy common sense, but it's still an assumption.
Now, suppose that in an argument for or against God that there are five premises. If the premises are independent of each other (and they should be, otherwise one of them isn't a premise), and each premise has a 50-50 chance of being correct, then the proof has a one in thirty-two chance of being correct. Those aren't great odds.
An immediate response to this would be, "but Euclidean geometry has five premises, and it's correct! So why not an argument for/against God with the same number of premises?" The answer is simple. We can measure the results of Euclidean geometry with a ruler and a protractor. While it's against the rules to construct something in Euclidean geometry with anything other than a straightedge and a compass, it isn't against the rules to check the result with measuring devices. And for non-Euclidean geometry, which is used in Relativity, we can measure it against the curvature of light around stars and the gravitational waves produced by merging black holes.
But we can't measure God, at least the non-physical God as God is normally conceived[6].
If that's the case, then it doesn't make sense to argue for/against the existence of God by any means other than "assume God does/does not exist". That gives a one in two chance of being right, as opposed to one in four, one in eight, ... one in 2^(number of premises).
If the premise "God does/does not exist" leads to a contradiction then, assuming the principle of (non)contradiction, the premise is falsified. I suspect, but cannot prove, that both systems are logically consistent. If this is so, then the search for God by formal argument is futile.
[Update:]
It seems to me that if the search for God by formal argument is futile, then the choice of axiom - God does/does not exist - is a logically free choice. And if it's a choice that you are not logically compelled to make, then it comes down to desire. [7]
[1] Can a Thomist Reason to God a priori?
[2] Commenting as "wrf3".
[3] I've informally taken this position here, here, here, and here.
[4] One unstated premise is usually, "common sense is a reliable guide to true explanations." It isn't. Relativity, and Quantum Mechanics, defy "common sense". Quantum Mechanics, for example, uses negative probabilities in the equations of quantum behavior. What's a negative probability? What's a "-20% chance of rain"? Yet we are forced by experiment to describe Nature this way.
[5] Quantum Mechanics also defies our common sense on causation, cf. "Quantum Mischief".
[6] Sentience/consciousness/the inner mind cannot be objectively measured. See The Inner Mind.
[7] For the desire to be fulfilled, God must then fulfill it. You can't tickle yourself. If you want to experience tickling, you must be tickled by someone else. If you want to experience God, then God must reveal Himself.
Electric Charge and the Laws of Thought
| Thought | Charge | |
|---|---|---|
| 1 | Identity | Like charges repel, opposite charges attract |
| 2 | Non-contradiction | Positive charge is not negative charge |
| 3 | Excluded Middle | Charge is either positive or negative |
Dialog with Jeff Williams: Intermission
I would ask you to demonstrate why reason is an atomic arrangement, and why it being a part of nature would imply truth; and along with that how you would explain erroneous ideas and the limits of the invariability principles.
Having written the first three (of five) parts, I think I've answered everything except "the limits of the invariability principles." To do that, I have to finish the posts on "meaning" and "math," then ruminate on the nature of infinity and its relationship to nature (a small part of the latter is here, but I also have some unpublished material on that, too).
Since I think I've answered all but the last (and I have every reason to believe that I can answer the last, but with a lot more exposition), I'm going to take a break to take time to mentally recharge before working on the next two parts.
Jeff can now attempt to rebut.
Table of Contents
- Jeff's original post
- Intro to my reply
- Part I to my reply
- Part IIa to my reply
- Part IIb to my reply
- Part III to my reply
- Intermission to my reply
Dialog with Jeff Williams: Part III
This is the third part to the answer of his question:
I would ask you to demonstrate why reason is an atomic arrangement, and why it being a part of nature would imply truth; and along with that how you would explain erroneous ideas and the limits of the invariability principles.
The answer will consist of five parts:
- The road to logic
- The road to truth
- Logic and Reason
- The road to meaning
- The road to math
This post will cover the third topic, Logic and Reason.
Read More...
Dialog with Jeff Williams: Part IIb
This is the second part to the answer of his question:
I would ask you to demonstrate why reason is an atomic arrangement, and why it being a part of nature would imply truth; and along with that how you would explain erroneous ideas and the limits of the invariability principles.
The answer will consist of five parts:
- The road to logic
- The road to truth
- Logic and Reason1
- The road to meaning
- The road to math
This post will cover the second topic, the road to truth.
Read More...
Dialog with Jeff Williams: Part IIa
Having set the stage, I will now answer his question:
I would ask you to demonstrate why reason is an atomic arrangement, and why it being a part of nature would imply truth; and along with that how you would explain erroneous ideas and the limits of the invariability principles.
The answer will consist of four parts:
- The road to logic
- The road to truth
- The road to meaning
- The road to math
This post will cover the first topic, the road to logic.
Read More...
Dialog with Jeff Williams: Part I
On his blog, Jeff has asked me to respond to several points.
But before he makes his specific request, he makes some preliminary statements, some of which I take issue with. He writes:
I recognize two distinct innate modes of human thought: rational objectification of events in the world; and esthetic experience of Being.
I agree with Jeff that we make distinctions between the sense data of our experiences, the description of what we think our sense data is telling us about an external world (assuming an external world exists!), and the description of how we think that sense data compares to an ideal (the esthetic experience). Where I disagree with Jeff is the nature of these distinctions.
We are all just "ripples on the quantum pond" (do take time to read this link. If we disagree on this we won't agree on the important things). So our sense data is ripples on the pond; our rational objectification of events is ripples on the pond, our esthetic experience is ripples on the pond; our "our" is ripples on the pond. For there to be true distinctions between these things then there needs to be true distinctions in the ripples.
This means that there are ripples that give rise to logic, truth, and meaning for these are the basis of our ability to describe events (Jeff's "rational objectification") and our ability to describe a "distance" between two events (which is the "is/ought" distinction). The only difference between the "rational objectification of events" and the "esthetic experience of Being" is that the latter involves a distance metric between two events or between an event and an "idealized" event.
The resulting representations do not exist as such in the external world...
Here, Jeff needs to demonstrate that there is an "external" -- as opposed to "internal" -- world. If everything is ripples on the pond, then the events and our descriptions of the events, all exist in the same pond. The "internal"/"external" distinction is due to the limitations of our perception and are not due to a fundamental aspect of reality.
I retain Heidegger’s distinction between them as “Truth” arising from esthetic experience, and “Correctness” inhering in objectification.
I note that Jeff needs to define what "truth" and "correctness" are in his worldview, just as I will have to do in mine. Mine is easy.
Again, Being is reduced to copula.
This is problematic for several reasons, which Jeff will have to defend. First, how does anyone know what "Being" is, since we can't directly experience it? Second, it betrays a form of thinking where "Being" and "copula" are distinct things. As a Christian, I would argue that this is equivalent to the "modalist" heresy. I don't want to immediately derail this particular part of the discussion, but we may eventually have to go there (cf. my posts on the Trinity, which are more about the ways this doctrine shows how individuals think about things than it is about the doctrine itself.).
Thankfully, we have no need to go through another tedious debate about duality.
I'm not sure we can ultimately escape it. As I (attempt to show) in On the Undecidability of Materialism vs. Idealism both physicalism and metaphysicalism are dual ways of looking at the same thing. If Jeff wants to get rid of metaphysics, then the only way he's going to be able to do it is by a subjective mental coin flip. That is, the only way you can get rid of metaphysics is by arbitrary fiat. Note the duality: the only way you can get rid of physicalism is by arbitrary fiat, too.
So now we get to the discussion points. Jeff wrote:
my claim that reason is essentially different from reality ...
Reason can't be different from reality, since it's all just ripples on the quantum pond1. What I think Jeff wants to say is that reason allows us to construct descriptions that may, or may not, accurately describe reality. The hard part is knowing which descriptions belong to which class. Jeff wants to reject the idea of "Being" and "copula", but he has to provide a basis as to why. Why not say that "Being" and "accurate descriptions of Being" are both "Being"? (note the parallel to Trinitarian thought).
I will repeat my original answer to that question: while we have dedicated receptors and neural paths for each sensation, no such thing exists for reason. I cannot experience reason the way I do light.
If reason is just the swirling of atoms in certain ways in your brain, then you have to be able to experience it, even if the connection may not be obvious. As I will show in the next blog post, you do have neural paths for reason. I'll show how they work in theory. That this works in practice can be seen in the paper "Computation Emerges from Adaptive Synchronization of Networking Neurons". And, if you're like other people (admittedly, my sample size is small), you experience reason by talking to yourself (we subvocalize our thoughts). That is, computation has to interact with it's environment for the results of computation to be known. The swirling atoms in your brain which are your reason interact with the sense receptors in your brain to make the results of reason known. That is, your sense receptors can be triggered by interaction with an external swirl of atoms as well as the internal swirl of atoms.
where I can create mathematics or logical forms, but this is entirely without external sense data.
I will show that this is false. You cannot sever the roots of mathematics from sense data. But I first have to show where you get logic, then truth, then meaning, and then math.
Without converting to the imaginings of space and time, I have no intuition of reason at all.
This, too, is false. One of the things that has to be understood is that, when it comes to physical devices, there is no difference between the hardware and the software. We may not know what initial knowledge the wiring of our brains gives us, but it's clear that it's there. See, e.g. "Addition and subtraction by human infants", Karen Wynn, Nature, Vol 361, 28 January 1993.
The new subject of quantum mind is attracting top physicists and neuroscientists and perhaps offers the path to understanding.
One the one hand, everything is quantum. On the other hand, let me quote Feynman:
Computer theory has been developed to a point where it realizes that it doesn't make any difference; when you get to a universal computer, it doesn't matter how it's manufactured, how it's actually made.2
That is, computer theory doesn't care about the actual physical construction details as long as you get the right behavior.
Your model, however, centers on atoms, not waves, and leaves the exact principles unspecified.
As per the Feynman quote, it doesn't matter if the model is based on atoms or waves. The model doesn't care. I'm going to use atoms simply because it's easier. And this is an interesting property, since whatever quantum "stuff" is, it exhibits wave-particle duality. That is, computation theory is wave-particle agnostic. What matters is the actual behavior.
and since atomic arrangements are part of nature, that implies an exact connection and description of truth.
Note quite. There is an exact connection between connection and description, but that doesn't mean that every description is true. Remember, there are false as well as true descriptions.
It would also leave unexplained the limitations of Wigner’s invariability principles, which seem to demonstrate the inability of reason to grasp anything larger than a very limited set of events within limited space and time.
Sure, our brains, being physical objects, have physical limitations on what they can keep in mind at one time. But the wonderful thing about Turing machines is that they can use external storage. In fact, to the best of my knowledge, man is the only animal that does use external storage for thoughts. We have all the physical bits in the universe by which we can augment our reason.
Instead, I would ask you to demonstrate why reason is an atomic arrangement ...
Better, reason is matter in motion in certain patterns. If you want to get a preview, see Notes on Feser's "From Aristotle..." If you have questions with this, I can try to address them in the next post.
[1] Unless, of course, you want to admit a transcendent God, who is reason itself and the non-physical cause of all physical things.
[2] Simulating Physics with Computers, International Journal of Theoretical Physics, Vol. 21. Nos. 6/7, 1982
Dialog with Jeff Williams: Intro
Eleven days later, the discussion is still going. I cobbled some code together to pull the entire conversation from this starting tweet, formatted it a bit, and saved it in a text file here.3 It helps immensely to be able to search the complete discussion for what has been said, to look for conversational loops, dead ends, and unanswered questions.
But the conversation has outgrown Twitter. At this point in Twitter, Jeff has asked me to defend one of my claims and has switched to his blog to continue this phase of the dialog. His post is here. After some preliminary remarks, I will respond directly here on my blog. If Twitter isn't a very good medium for these kinds of things, neither are a blog's commenting facilities, particularly since I'm going to want to use diagrams to illustrate some points.
Why have Jeff and I been doing this for almost two weeks now? I won't speak for Jeff but, while I thoroughly disagree with some of his fundamental statements and think that his worldview is ultimately incoherent, we do agree in some surprising ways. For example, he posted a rebuttal to some arguments made by the Christian apologist William Lane Craig. While I don't agree with everything in his rebuttal, I do agree that Craig (as well as most contemporary apologists) are an embarrassment. I'll try my best not to join them.
I also agree that reality, whatever it is, is deeply counterintuitive. I've posted Feynman's comments about the nature of nature from his lecture on quantum mechanics before (e.g here and here). They are1:
We see things that are far from what we would guess. We see things that are very far from what we could have imagined and so our imagination is stretched to the utmost … just to comprehend the things that are there. [Nature behaves] in a way like nothing you have ever seen before. … But how can it be like that? Which really is a reflection of an uncontrolled but I say utterly vain desire to see it in terms of some analogy with something familiar… I think I can safely say that nobody understands Quantum Mechanics… Nobody knows how it can be like that.
This leads me to sympathy for Jeff's statement:
The strangeness of physics presents unmatched opportunities for philosophy at this moment. I regret that few mathematicians and scientists have reciprocated with an understanding of philosophy, which always precedes other fields by clearing and setting the grounds for thinking in any age.2
But I will expand on that in that we all need each other. Philosophers need to incorporate what we know of the physical world into their philosophies (assuming they want them to be correct descriptions of reality, for some definition of "correct"), and scientists need to do the same. Because sometimes they share the same goal: to figure out what we really know and how we know that we know it.
I found Jeff's post "Response to Eckels on Heidegger and Being" a welcome companion to illuminate some of the things he said on Twitter. Some (hopefully helpful) material to provide background on what I hope to say in more depth in my reply is here. I expect that it will take me a few days to put things in a satisfactory arrangement.
[1] "The Character of Physical Law - Part 6 Probability and Uncertainty"
[2] Part one and part two.
[3[ Updated 9/22/20 since the conversation is still ongoing.
On the Undecidability of Materialism vs. Idealism
According to Douglas Hofstadter1:
What is a self, and how can a self come out of the stuff that is as selfless as a stone or a puddle? What is an "I" and why are such things found (at least so far) only in association with, as poet Russell Edison once wonderfully phrased it, "teetering bulbs of dread and dream" .... The self, such as it is, arises solely because of a special type of swirly, tangled pattern among the meaningless symbols. ... there are still quite a few philosophers, scientists, and so forth who believe that patterns of symbols per se ... never have meaning on their own, but that meaning instead, in some most mysterious manner, springs only from the organic chemistry, or perhaps the quantum mechanics, of processes that take place in carbon-based biological brains. ... I have no patience with this parochial, bio-chauvinist view...
According to the Bible2:
In the beginning was the Word, and the Word was with God, and the Word was God. ... And God said, "Let there be light"; and there was light.
I believe that computability theory, in particular, the lambda calculus, can shed some light on this problem.
In 1936, three distinct formal approaches to computability were proposed: Turing’s Turing machines, Kleene’s recursive function theory (based on Hilbert’s work from 1925) and Church’s λ calculus. Each is well defined in terms of a simple set of primitive operations and a simple set of rules for structuring operations; most important, each has a proof theory.3
All the above approaches have been shown formally to be equivalent to each other and also to generalized von Neumann machines – digital computers. This implies that a result from one system will have equivalent results in equivalent systems and that any system may be used to model any other system. In particular, any results will apply to digital computer languages and any of these systems may be used to describe computer languages. Contrariwise, computer languages may be used to describe and hence implement any of these systems. Church hypothesized that all descriptions of computability are equivalent. While Church’s thesis cannot be proved formally, every subsequent description of computability has been proved to be equivalent to existing descriptions.
It should be without controversy that if a computer can do something then a human can also do the same thing, at least in theory. In practice, the computer may have more effective storage and be much faster in taking steps than a human. I could calculate one million digits of 𝜋, or find the first ten thousand prime numbers, but I have better things to do with my time. It is with controversy that a human can do things that a computer, in theory, cannot do.4 In any case, we don't need to establish this latter equivalence to see something important.
The lambda calculus is typically presented in two parts. Lambda expressions and the lambda expression evaluator:
![]()
One way to understand this is that lambda expressions represent software and the lambda evaluator represents hardware. This is a common view, as our computers (hardware) run programs (software). But this distinction between software and hardware, while economical and convenient, is an arbitrary distinction which hides a deep truth.
Looking first at 𝜆 expressions, they are defined by two kinds of objects. The first set of five arbitrary symbols: 𝜆 . ( ) and space represent simple behaviors. It isn't necessary at this level of detail to fully specify what those behaviors are, but they represent the "swirly, tangled" patterns posited by Hofstadter. The next set of symbols are meaningless. They represent arbitrary objects, called atoms. Here, they are characters are on a screen. They can just as well be actual atoms: hydrogen, oxygen, nitrogen, and so on.
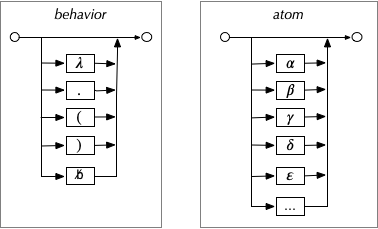
The only requirement for atoms is that they can be "strung together" to make more objects, here called names (naming is hard).

With these components, a lambda expression is defined as:
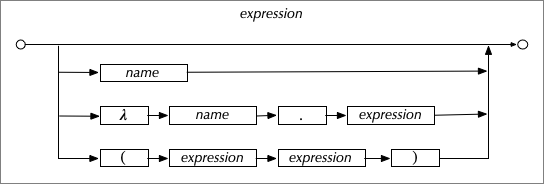
Note that a lambda expression is recursive, that is, a lambda expression can contain a lambda expression which can contain a lambda expression, .... This will become important in a future post when we consider the impact of infinity on worldviews.
With this simple notation, we can write any computer program. Nobody in their right mind would want to, because this notation is so tedious to use. But by careful arrangement of these symbols we can get memory, meaning, truth, programs that play chess, prove theorems, distinguish between cats and dogs.
Given this definition of lambda expressions, and the cursory explanation of the lambda expression evaluator (again, see [3] for details), the first key insight is that the lambda expression evaluator can be written as lambda expressions. Everything is software, description, word. This includes the rules for computation, the rules for physics, and perhaps even the rules for creating the universe.
But the second key insight is that the lambda evaluator can be expressed purely as hardware. Paul Graham shows how to implement a Lisp evaluator (which is based on lambda expressions) in Lisp. And since this evaluator runs on a computer, and computers are logic gates, then lambda expressions are all hardware. With the right wiring, not only can lambda expressions be evaluated, they can be generated. We can (and do) argue about how the wiring in the human brain came to be the way that it is, but that doesn't obscure the fact that the program is the wiring, the wiring is the program. That we can modify our wiring/programming, and therefore our programming/wiring, keeps life interesting.
Therefore, it seems that materialism and idealism remain in a stalemate as to which is more fundamental. It might be that dualism is true, but I think that by considering infinity that dualism can be ruled out as an option, as I hope to show in a future post.
[1] Gödel. Escher, Bach: an Eternal Golden Braid, Twentieth-anniversary Edition; Douglas R. Hofstadter; pg. P-2 & P-3
[2] The Bible, New Revised Standard Version, John 1:1, Genesis 1:3
[3] An Introduction to Functional Programming Through Lambda Calculus, Greg Michaelson
[4] This would require a behavior we cannot observe; a behavior we can't describe; or a behavior we can't duplicate. If we can't observe it, how do we know it's a behavior? A behavior that we can't describe would mean that nature is not self-describing. That seems impossible given the flexibility of description, but who knows?. There might be behaviors we can't duplicate, but that would mean that nature behaves inside human brains like it can behave nowhere else. But there just aren't examples of local violation of general covariance, except by special pleading.
Update 9/30/20
In The Emperor's New Mind, Richard Penrose muses:How can concrete reality become abstract and mathematical? This is perhaps the other side of the coin to the question of how abstract mathematical concepts can achieve an almost concrete reality in Plato’s world. Perhaps, in some sense, the two worlds are actually the same?
Note the unexamined bias. Why not ask, "how can the abstract and mathematical become concrete?" In any case, they can't be the same, since infinity is different in both.
Epistemology & Hitchens
... Reformed theology regards the existence of God as an entirely reasonable assumption, it does not claim the ability to demonstrate this by rational argumentation. Dr. Kuyper speaks as follows of the attempt to do this: “The attempt to prove God’s existence is either useless or unsuccessful."
Let me now attempt to put some theory behind these musings.
A Twitterer attempted to take Christopher Hitchens to task for his statement:
What can be asserted without proof can be dismissed without proof.
Hitchens isn't wrong, but his statement is incomplete. The corrected version should read:
What can be asserted without proof can be accepted or dismissed without proof.
Why is this so? Because reason has to start somewhere. It has to hold that some fundamental, foundational, things are true simply because they are true. They are the first stepping stone on what may be a long journey.
It may be that an axiom results in a system that conflicts with empirical measurement. In that case, the axiom can be rejected (or the measurement questioned). It may be that the axiom agrees with empirical measurement. In that case, it can continue to be provisionally accepted for as long as no other disconfirming empirical measurement is found. Note that empirical agreement with one axiom does not rule out other axioms that have the same empirical agreement.
It may be that an axiom conflicts with other axioms or statements derived from those axioms. In that case, something has to give. Knowing what has to give can be problematic.
But it may also be the case, thanks to Gödel and the universe, that we can never fully explore the consequences of the axiom either logically or empirically. In that case, you are free to accept it or reject it.
I submit for your consideration that the axiom of "God" is in the latter category. You are free to accept or reject as you will. It may be one of the few truly free choices you get to make in life. In thousands of years there has been no successful logical proof of God's existence, nor has there been a successful logical proof of God's non-existence. Neither is there any generally accepted empirical proof either way. Note that I put self-reflection in the category of empirical proof.
But this means I also have to finish my examination of the Warren-Flew debate to show why Flew ultimately failed.
Warren-Flew Debate, Part 2
In my previous post, I lamented that neither side addressed what it means to know. Still, Flew made some observations which deserve comment.
On Knowledge
That is to say we have to start from and with our common sense and our scientific knowledge of the universe around us.
Yes, we all have to start somewhere. But we need to establish criteria on how we know we've arrived. With common sense, Flew fails to establish whether the majority view (theism) or the minority view (atheism) is the "common" one. One can do an internet search for "humans hardwired religion" and see the arguments for and against. The argument against says that humans are hardwired for pattern recognition, but this misses the point. After recognizing patterns, we seek teleology. And we are wired for teleology - we have to be - but atheists suppress this aspect of being.
As to scientific knowledge, scientific knowledge is incomplete and sometimes wrong. This is not to disparage science; it's just the nature of the thing. Too, scientific knowledge contains descriptions based on empirical induction, and descriptions from empirical induction are probabilistic. That means that there is some point where we consider a probability high enough to be trustworthy - whether it's 50.1%, 75%, or 99.9999%. And this leads to the necessity of what it means to trust Nature and whether or not Nature is trustworthy. Note that the same considerations apply to questions about God.
Of equal importance is the trustworthiness of our intuitions. Feynman gives an idea of inability of intuition to grasp quantum mechanics. In his hour long lecture "The Character of Physical Law - Part 6 Probability and Uncertainty", he begins by saying that the more that we observe Nature, the less reasonable our explanations of Nature become. "Intuitively far from obvious" is one phrase he uses. Within the first ten minutes of the lecture he says things like:
We see things that are far from what we would guess. We see things that are very far from what we could have imagined and so our imagination is stretched to the utmost … just to comprehend the things that are there. [Nature behaves] in a way like nothing you have ever seen before. … But how can it be like that? Which really is a reflection of an uncontrolled but I say utterly vain desire to see it in terms of some analogy with something familiar… I think I can safely say that nobody understands Quantum Mechanics… Nobody knows how it can be like that.
Neither Flew nor Warren acknowledged the problem of intuition getting in the way of apprehending truth, nor possible approaches for dealing with it. We'll see how this problem affects Flew's Euthyphro argument.
About the law of the excluded middle: in general surely it can only be applied to terms and contrasts which are adequately sharp.
This is quite true. Logic, and computation, are based on objects that are distinguishable. This means that if two things can't be distinguished, then we can't accurately describe them. This means that God is beyond reason and logic, because He is not made of distinguishable parts, yet we talk about Him as if He is. At the heart of the Christian concept of God is what is to us a paradox: what God says is the same as what God is (because both are immaterial and unchanging), yet what God says is somehow different from what God is. Flew doesn't mention if this difficulty - that God is beyond reason - is one of the things that enters into his affirmation that there is no God.
My first and very radical point is that we cannot take it as guaranteed that there always is an explanation, much less that there always is an explanation of any particular desired kind.
Bravo, except that this shouldn't be radical. We know that empirical knowledge is incomplete (we'll never experience the interior of a black hole, at least not in any way we can talk about it) and, ever since Gödel, we know that knowledge based on self-referential logic is incomplete.
You can not argue: from your insistence that there must be answers to such questions; to the conclusion that there is such a being.
This. A thousand times this. Explanations are "just so" stories of which there can be no end. "Just so" stories that actually describe reality are much harder to devise.
For in the nature of the case there must be in every system of thought, theist as well as atheist, both things explained and ultimate principles which explain but are not themselves explained.
Note that Warren says the same thing: "God is the explanation which needs no explanation." In the final analysis, both sides end up with what they start with! Flew starts with "no god" and ends with "no god"; Warren starts with "god" and ends up with "god". Everything else in between are flawed arguments. I hope that once you see this happen, time and time again, that you see that what passes for a lot of "apologetics" are vain attempts to prove what has been assumed as true!
How often and when, when you make a claim to know something or other, do you undertake or expect to be construed as undertaking to provide a supporting demonstration of the kind which Dr. Warren so vigorously and so often challenges me to provide? Certainly when we claim to know anything, we do lay ourselves open to the challenge to provide some sort of sufficient reason to warrant that claim. But that sufficient reason can be of many kinds. And, although it may sometimes include some deductive syllogistic moves, the only case I can think of offhand in which a syllogism is the be-all and end-all of the whole business is that of a proposition in pure mathematics. Clearly that is not the appropriate model in the present case.
Again, Flew is right. The problem is that he doesn't say what the appropriate model is. He doesn't provide the testability criteria that he demands must be present (covered in the the next post).
The other way, which is the interesting one which I want to consider, is to urge that whereas we who have not enjoyed the revelatory experiences vouchsafed to the believer cannot reasonably be required to accept his claims, this believer himself is in a sure position to know.
Flew is basically saying that the "deaf" don't need to trust the "hearing". Here, Flew says "I haven't heard". Later, he will say, "I don't see." While he admits these things, he then needs to show that the theist is hallucinating and examine whether or not his presumption of atheism is the cause of his not hearing or seeing. As anyone who does puzzles knows, changing how you look at the puzzle can enable you to see things previously missed.
Flew gets positive marks for trying to lay a foundation of what it means to know; but negative marks for the incompleteness of his presentation. Having reviewed these points, the next post will examine Flew's three arguments.
Warren-Flew Debate, Part 1
Somewhere, in a place that I can no longer find1, I remember reading that Antony Flew was the "most important atheist you've never heard of." On the other hand, Flew may have abandoned atheism in favor of deism in 2004, six years before his death. One side says the switch may have been the result of senility - a charge which Flew denied2. Still, up until that point, he had an impressive pedigree. And in 1976, he debated Thomas Warren over a period of four nights in Denton, Texas where he argued for the affirmative position that there is no God. The debate is available on Youtube and in print.
My primary goal will be to examine Flew's arguments. My secondary goal will be to dissect Warren's responses to Flew. I have to admit that my sympathies -- but not my worldview -- are with Flew in the debate. My impression is that, of the two debaters, he is the more careful craftsman. He is trying to paint a picture with careful brush strokes while Warren is firing a paint gun. Flew is wielding a scalpel, while Warren is using a chain saw. Both have their uses, even though Flew removes the wrong organ and Warren cuts down the wrong tree.
Because my sympathy is with Flew I will deal with his arguments last. First, I want to show where Warren's responses to Flew fall flat. First, Warren makes the claim that Flew has to hurdle seven walls; escape seven cages, to "know" that God does not exist. Warren presents his chart number 9 (manually recreated with minor edits):
And this leads to a fundamental problem. Neither side addresses what it means "to know". There is no mutual groundwork on the nature and limits of reason, empiricism, or self-evident knowledge. Warren has a way that he escapes the mutual prison cells, but I suspect he wouldn't permit Flew to use the same kind of tools. Warren says:
...the only way he can arrive at atheism is to come through all of these walls.
This simply isn't true. We know that knowledge obtained by empiricism is incomplete, if only because we can't experience everything. Thanks to Kurt Gödel, we know that knowledge obtained by reason, if it is consistent, is incomplete3. Both Warren and Flew need to address what it means to know in the face of uncertainty.
There are some things that we just can't know. And some of the things we claim to know by reason are built upon statements that are taken to be true for no other reason than they are assumed to be true. These axioms, these presuppositions, these self-evident truths may, or may not, conform to external reality (whatever that turns out to be4.) So while something might be logically true, it may not correspond to a correct description of Nature (cf. the "Stoddard" portion of the Spock-Stoddard Test).
Too, each system may give different answers to the same questions5, and a question that has an answer in one system might not have an answer in another. It's important to watch for mental sleight of hand when someone argues the superiority of one system over another because their system has an answer to something the other does not. That's not necessarily a virtue. Their system will have unanswerable questions that might be answered in their opponents system.
Warren will use this technique ("my worldview has an explanation, but Flew's does not") as if this settles the matter. As above, it does not. Furthermore, wittingly or unwittingly, this leads to "God of the gaps" thinking. That is, the idea God has nothing better to do than to be an explanation for things where our knowledge is incomplete. While our knowledge will always be incomplete, the moment a particular gap in our knowledge closes, the need for God in that particular instance goes away. So much for an unchanging God.
Warren also seemed to refuse to accept the problem of the Sorites paradox, that is, the lack of bright lines of demarcation between some objects. How many grains of sand comprise a pile? How many hairs on a head make the difference between bald and hirsute? In the theory of evolution, where did the difference between human and non-human occur? Warren states:
The truth of the matter is, the theist, who believes in Almighty God, has absolutely no trouble with the question of which was first--a woman or a baby.
Sure, but this is because Genesis gives an account where this question is answered. But, as stated before, just because there is an answer doesn't mean it corresponds to reality. The existence of an explanation is not evidence of the truth of the explanation. Warren then asks:
Have you ever seen anything that was neither human nor non-human?
Here, Warren is begging the question. What, exactly, does it mean to be human? That we have the form of a human? Clearly, the Sorites paradox comes into play, since a person who is missing limbs isn't less human than than someone who isn't. Is it based on behavior? If I lose my mind to dementia, does my humanity gradually fade? If something passes the Turing Test, can it be said to be human? Is humanity based on genetics? Neanderthal and modern humans apparently had a common ancestry. In practice, we find that the definition of human is fluid. It depends on form -- except when it doesn't. It depends on behavior -- except when it doesn't. It depends on genetics -- except when it doesn't. Warren ought to admit that our humanity is rooted in our being in the image of God -- but this has to be something non-physical. And since it's non-physical, it's hard to define. Warren is using a sharp line which his own theology has to affirm is actually ineffable.
To be continued...
[1] Possibly "Did Jesus Rise from the Dead?: The Resurrection Debate", Habermas and Flew.
[2] Asking the senile if they're senile is like asking a drunkard if he's drunk, or an insane person if he's insane.
[3] Gödel's first incompleteness theorem.
[4] The Matrix
[5] Compare Euclidean and non-Euclidean geometries.
The Zeroth Commandment
I am the LORD your God. You shall have no other reasons before Me.
Spock-Stoddard Test
It is not logical, but it is often true.
-- Spock, "Amok Time"
It’s logical, but I wonder if it’s correct?
-- Elizabeth Collins Stoddard, "Dark Shadows", #132
Update 9/26/20. Nothing is new. I came across this on Twitter, which came from here:
Something can sound very logical and still be false. Or something may sound unbelievable and be true.
-- Octavius, 200 A.D.
Notes on Feser's "From Aristotle..."
[updated 1/24/2025 to add link to Woodrush]
Some notes on Edward Feser's "From Aristotle to John Searle and Back Again: Formal Causes, Teleology, and Computation in Nature". This is not a detailed rebuttal; rather it's an outline of points of disagreement with various statements in his paper. To better understand why I disagree the way I do, previous experience with the lambda (λ) calculus is helpful. Reviewing my disagreement with Searle's Chinese Room Argument may also be useful. I wrote that article over a year ago and promised to revisit it in more detail. One of these days. Still, my understanding of Searle's argument is this:
We can, in theory, construct a machine that can translate from Chinese to another language, without it understanding Chinese. Therefore, we cannot construct a machine that can both translate and understand Chinese.
The conclusion simply doesn't follow and I don't understand how it manages to impress so many people. One possibility is confirmation bias.1 Fortunately, one of the Fathers of computer science, John McCarthy, independently came to the same conclusion. See "John Searle's Chinese Room Argument".
Feser makes the same kinds of mistakes as Searle.
Syntax is not sufficient for semantics.
From John Searles's Chinese Room paper, quoted by Feser.
True, but incomplete. The λ calculus has syntax (λ expressions) and semantics (λ evaluation).
The problem is this. The status of being a "symbol," Searle argues, is simply not an objective or intrinsic feature of the physical world. It is purely conventional or observer-relative.
- This is exactly right, that is, it is observer-relative but this isn't a problem. In the λ calculus, meaning is the arbitrary association of a symbol with another set of arbitrary symbols. It is simply an arbitrary association of this with that. What Searle and Feser miss is that the most fundamental thats are our sense impressions of the (presumably) external world. Because our brains are built mostly the same way, and because we perceive nature in mostly the same way, we share a common set of "this with that" mappings, upon which we then build additional shared meaning.
- This is why there is no problem with qualia. It doesn't matter how a brain encodes this and that. it is the association that determines meaning, not the qualia themselves. (See here).
- In the final analysis, nature observes itself, since we observers are a part of nature. As the Minbari say, "We are 'star stuff.' We are the universe, made manifest - trying to figure itself out."
It's status as a "computer" would be observer-relative simply because a computer is not a "natural kind," but rather a sort of artifact.
- First, as Feynman wrote, "Computer theory has been developed to a point where it realizes that it doesn't make any difference; when you get to a universal computer, it doesn't matter how it's manufactured, how it's actually made."2
- We have been made by nature. We can, and likely will, argue forever over how this actually happened, but this paper cannot concern itself with either "why does the universe exist?" or "why does the universe exist the way it does?".
- We observe ourselves ("Cogito ergo sum").
In short, Searle says, "computational states are notdiscovered within the physics, they are assigned to the physics.
- I think this betrays "linear parallel" thinking. This is "this" and that is "that" and the two don't meet. But what Searle and Feser miss is that nature is self-referential. Nature can describe itself. And that's why the objection, "Hence, just as no physicist, biologist, or neuroscientist would dream of making use of the concept of a chair in explaining the natural phenomena in which they deal, neither should they make use of the notion of computation." is wrong.
- Chairs aren't self-referential objects. Computation, and intelligence, -- and nature -- are. Recursion is fundamental to computation. In implementing a λ calculus evaluator, Eval calls Apply; Apply calls Eval. We may (or may not) not use the concept of "chair" to explain natural phenomena, but we can't escape using the concept of intelligence to explain intelligence. This computer science aphorism is instructive: to understand recursion you must first understand recursion.
For, whatever we say about whatwe mean when we use terms like "plus," "addition," and so on, there are no physical features of a computer that can determine whether it is carrying out addition or quaddition, no matter how far we extend its outputs.
This is, of course, false. The programming is the wiring. One could, in theory (although it might be nigh impossible in practice to untangle how symbols flow through the wires), recover the method by reverse engineering the wiring. Then one could determine whether addition or quaddition was being performed. Since the methods are different, the wiring would be different.
[Searle] is not saying, whether there are [rigourously specifiable empirical criteria for whether something ... is a computer] or not, that something fitting those criteria counts as a computer is ultimately a matter of convention, rather than observer independent facts.
How nature behaves is empirical fact. Putting labels on different aspects of that behavior is a matter of convention. Searle is objecting to the very nature of nature.
[Searle holds] that having a certain physical structure is anecessary condition for a system's carrying out a certain computation. Searle's point, though, is that is nevertheless not a sufficient condition.
This is false for systems that compute. For the example of a Turing machine, the wiring, the physical structure, is both necessary and sufficient. It is a self-referential structure. For systems with less computational power than a Turing machine, the wiring will be simpler.
If evolution produced something that was chair-like, it would not follow that it had produced a chair, and if evolution produced something symbol like, it would not follow that it had produced symbols.
- First, this is the Sorities paradox on display. At what point is something like x actually x? It depends on definitions and definitions can be fuzzy.
- Second, and absolutely devastating to Feser's argument, is that in the λ calculus, symbols are meaningless.
- Third, in the λ calculus, symbols are nothing more than distinct objects. And nature is full of distinct objects that can be used as symbols. Positive and negative charge is important because they are distinguishable and they are self-distinguishing!
- Fourth, how evolution builds a self-referential structure in which symbols acquire meaning is through the equivalent of λ evaluation is, of course, contentious.
If the computer scientist's distinction between "bugs" and "features" has application to natural phenomena, so too does the distinction between "software" and "hardware."
The λ calculus consists of λ expressions and λ evaluation. λ evaluation is just a list of substitution rules for symbols, and symbols are just distinguishable objects. In this sense, the program (λ expressions) and computer (λ evalution) distinction exists. However, λ evaluation can be written in terms of λ expressions. And here the program/computer distinction disappears. It's all program (if you observe the behavior) and it's all computer (if you look at the hardware). A λ calculus evaluator can be written in the λ calculus (see Woodrush and Paul Graham's The Roots of Lisp) which is then arranged as a sequence of NAND gates (or whatever logic gates you care to use. Cf. the Feynman quote, above). So it's very hard to know if something is a "bug" or a "feature" from the standpoint of the computer. It's just doing what it's doing. It's only as you impose a subjective view of what it should be doing, and how it should do it, that bugs and features appear. Nature says "reproduce" (if one may be permitted an anthropomorphism). And nature has produced objects that do that spectacularly.
But no such observer-relative purposes can be appealed to in the case of the information the computationalist attributes to physical states in nature.
The λ calculus simply specifies a set of symbols and the set of operations on those symbols that comprise what we call computation. What needs to be understood is that symbols as meaningless objects and symbols as meaning are the same symbols. The λ calculus does not have one set of symbols that have no meaning and another set of symbols that have meaning. There is only one alphabet of a least two different symbols. If you follow a symbol through a computational network, you can't easily tell at some point in the network, whether the object is being used as a symbol or if it's being used as a value. Only the network knows. We might be able to reverse engineer it by painstaking probing of the system, but even there our efforts might be thwarted. After all, a symbol could be used one way in the network and a completely different way in another part of the network. That is, computers don't have to be consistent in the way they use symbols. All that matters is the output. Even our computing systems aren't always consistent in the way things are arranged. For example, when little-endian systems interface with big-endian peripherals. Due to the complexity of "knowing" the system from the outside, you have to hope that the system can tell you what it means and that you can translate what it tells you into your internal ideas of meaning. I can generally understand what my dog is telling me, but that's because I anthropomorphize his actions. I have to. It's the only way I can "understand" him.
Moreover, as John Mayfield notes, "an important requirement for an algorithm is that it must have an outcome," and "instructions" of the sort represented by an algorithm are "goal-oriented."
- It is true that algorithms must terminate. That's the definition of "algorithm".3 But algorithms are a subset of computing. A computational process need not terminate.
- All computing networks are goal oriented. The fundamental unit of computation is the combination of symbols and selection therefrom. By definition, the behavior introduces a direction from input to output, from many to fewer. (One might quibble that the idea of inversion takes one symbol and produces the "opposite" symbol, but one can implement "not" using "nand" gates, and "nand" gates are goal oriented.) So if logic gates are goal oriented, systems built out of gates are goal oriented. The goal of the individual gate may be determinable; determining the goal of the system built out of these elements can be extremely difficult, if not impossible to fathom. Sometimes I understand my dog. Other times, all I see is emptiness when I look into his eyes. All we can do is compare the behavior of a system (or organism) to ours and try to establish common ground.
The information content of the output [of a computation] can be less than the input but not greater.
True, but irrelevant for systems that get input from the environment. That is, computers need not be closed systems. With the correct peripherals, a computer can take as input all of the behavior of the universe.
Darwin's account shows that the apparent teleology of biological process is an illusion.
- Underlying this claim is the idea that randomness exhibits purposelessness.
- However, one can also equally make the claim that randomness hides purpose. As Donald Knuth wrote, "Indeed, computer scientists have proved that certain important computational tasks can be done much more efficiently with random numbers than they could possibly ever be done by deterministic procedure. Many of today's best computational algorithms, like methods for searching the internet, are based on randomization."4
- Whether someone thinks randomness is purposeless or hides purpose is based on one's a priori worldview.
The key is to reject that [mechanistic] picture and return to the one it supplanted [Aristotle-Scholastic].
The fallacy of the false dilemma. Another alternative is to deeply understand the "mechanistic" picture for what it actually says.
[1] Battlestar Galactica: "I'm not a Cylon..."
[2] Simulating Physics with Computers, International Journal of Theoretical Physics, Vol. 21. Nos. 6/7, 1982
[3] The Art of Computer Programming, Volume 1: Fundamental Algorithms, Section 1.1; Donald Knuth
[4] Things A Computer Scientist Rarely Talks About
Ravi Zacharias on Objective Morality
This is an flawed answer, simply because people don't always do what they know they should do. That is, if morals are objective, people won't always act morally1, and if morals are subjective, then people won't always act morally2. Therefore, this answer has no bearing on the question!
Ravi further states:
If morality is purely subjective then you have absolutely nothing from stopping anybody from being a subjective moralist to choose to just zing one through your forehead and say 'that's my answer.'" How do you stop that? If you're willing to say to me that moral reasoning can be purely subjective, I just say to you, "look out, you ain't seen nothing yet."
This answer fails for (at least) four reasons.
First, it's the fallacy of the "appeal to consequences." That is, the desirability of something generally has no bearing on whether or not a statement is true or false. The statement "it is true (or false) that morals are subjective" is not proved by "subjective morality isn't desirable."
Second, it requires an appeal to authority. After all, who says that "subjective morality isn't desirable?" Ravi? The listener?3 God? For an appeal to authority to have some credibility, everyone has to agree on the authority. Atheists certainly don't agree that God carries any authority.
Third, Ravi knows that governments wield the sword against "evildoers".4 "Wield the sword." "Zing one through the forehead". Same difference. When Paul wrote this, the citizens didn't get to choose the kind of government they had or what the government thought was good and evil. Paul was imprisoned and eventually executed by that government.5
Fourth, and most importantly, Ravi should know the answer to "how do you stop that?" By preaching the gospel, that's how. God pours His love into the hearts of those who believe and "love does no wrong to a neighbor."6
That this particular response does not adequately address whether morals are objective, does not prove that they are subjective. After all, there could be a better answer. One would have hoped that a renowned apologist would have had a better response.
[1] The initial course, "Introduction: First Five Lessons" in the Open Yale course Game Theory, shows where students are asked to play a game. Most of them don't know, and therefore don't use, the optimal strategy when they first play the game. But after the instructor analyzes the problem and shows them the objective answer -- the right thing to do -- some of them still don't make that choice!
[2] See Another Short Conversation...
[3] I once had a conversation with an Indian coworker. He didn't understand why the US didn't nuke Pakistan in order to take out Bin Laden. When I replied that the fallout would take out tens, if not hundreds, of thousands of his countrymen he responded, "So what? They're just surplus people." What horrified me was a desirable outcome for him.
[4] Romans 13:4.
[5] Genesis 50:20
[6] Romans 13:10.
A Physicist's Questions
... most of the things that we consider to be intrinsic and instinctive human values are actually nothing of the sort; they are primarily and fundamentally the product of Christianity and would not exist without the last 2000 years of Christian dominance on our culture.
Today, in Creation Myths, by Marie-Louise Von Franz, I read:
Always at bottom there is a divine revelation, a divine act, and man has only had the bright idea of copying it. That is how the crafts all came into existence and is why they all have a mystical background. In primitive civilizations one is still aware of it, and this accounts for the fact that generally they are better craftsmen than we who have lost this awareness.
This suggests the more general case of a connection with the divine producing better results.
And this triggered the memory of an article by Dr. Lubos Motl written in 2015, "Can Christians be better at quantum mechanics than atheists"? Lubos makes some interesting statements. First, he answers his question generally affirmatively: "Apparently, yes." On the other hand, Lubos is an atheist and is an expert on quantum mechanics. Still, he notes:
In this sense, atheism is just another unscientific religion, at least in the long run.
"In this sense" being atheistic eisegesis, where the atheist attempts to impose their own prejudices onto Nature, instead of the other way around. Note that the Christian has this problem in double measure: not only must Christians avoid molding Nature into their own image, they must avoid molding God into their own image. They must be conformed to the Word, not conform the Word to themselves. Idolatry is a sin in both science and theology.
Nevertheless, in his post, Lubos asks some questions about Christianity that I'm going to attempt to answer. First, he asks:
A church surely wants the individual sheep to be passive observers, doesn't it?
Of course not. The church is a group of people who have been given a mission: to love one another and to make disciples throughout the entire world. We are to be active participants in the kingdom life. We don't "create our own world", but we don't do this in quantum mechanics, either. In both cases, the world reveals itself to us. After all, Wigner will get the same result as his friend.
But underneath Lubos' question is the idea of control: control by the church upon individuals and Lubos don't like outside control. He becomes rightfully incensed about suggestions, for example, that some questions should be off-limits to scientific inquiry. Yet consider one of the over-arching themes of the Bible, namely, order from chaos, harmony from static. This theme begins in Genesis and continues through Revelation. Static is maximally free. It cannot be compressed, there are no redundancies. Harmony requires a giving up of freedom. Totalitarians, whether secular or misguided Christians, will try to impose this order from without. Christianity says that this order must come from within, by the indwelling Spirit of God, received through the Lord Jesus Christ. It cannot be imposed by force of arms, but only through the reception of the Gospel. Each believer must find their own place(s) in the heavenly music.
But don't all religions actually want the only objective truth about the state of Nature to exist?
What we may want, and what actually is, are two different things. Still, Christianity says that we live by faith. This means we are uncertain as to what may come our way, even though we are certain as to God's faithfulness. As St. Paul wrote to the Corinthians, "for we see as though a glass, darkly."
Classical physics was doing great with omniscient God while quantum mechanics with its observer-dependence (and therefore "relativism" of a sort) seems to be more heretical, doesn't it?
Christianity is, in a sense, observer dependent, too. It claims that there are those who do not experience God and those who can. There are blind who do not see and deaf who do not hear. Furthermore, it claims that those who do not experience God cannot, unless God first works in them to restore their "spiritual" senses. But Lubos' question about omniscience contains a fact not in evidence, namely, that what we cannot foreknow (the outcome of a measurement before the measurement), God cannot also foreknow. There are no "hidden variables" in the natural world, but Scripture claims that there is hidden knowledge known only to God (eg. Dt. 29:29, et. al.) So on this point, the Christian and Dr. Motl will just have to disagree.
Science is ultimately independent of the religions – but it is independent of other philosophies such as the philosophies defended by the atheist activists, too.
Maybe. Science sees one part of the elephant, philosophy another. Until we have one theory of everything, I think this should remain an open question. I think Escher's Drawing Hands applies more to the relationship between science and philosophy than we might want to admit.
Reason, Empiricism, Self-Reference
“Reacting against the rationalism of Descartes, Spinoza and Leibniz, British philosophers dismissed the idea that reason is our only reliable source of knowledge and developed the opposing movement known as empiricism. While not denying that reasoning is important to assessing information, the empiricists believed that the source of that information is the outside world, accessed through our senses.”
Certainly, it would be nice to be able to explain the value of the fine-structure constant by reason and not by measurement. As Feynman observed:
“There is a most profound and beautiful question associated with the observed coupling constant, e – the amplitude for a real electron to emit or absorb a real photon. It is a simple number that has been experimentally determined to be close to 0.08542455. (My physicist friends won't recognize this number, because they like to remember it as the inverse of its square: about 137.03597 with about an uncertainty of about 2 in the last decimal place. It has been a mystery ever since it was discovered more than fifty years ago, and all good theoretical physicists put this number up on their wall and worry about it.) Immediately you would like to know where this number for a coupling comes from: is it related to pi or perhaps to the base of natural logarithms? Nobody knows. It's one of the greatest damn mysteries of physics: a magic number that comes to us with no understanding by man. You might say the "hand of God" wrote that number, and "we don't know how He pushed his pencil." We know what kind of a dance to do experimentally to measure this number very accurately, but we don't know what kind of dance to do on the computer to make this number come out, without putting it in secretly!"
See also, Parameters of Nature, which asks the question:
“Can all fundamental dimensionless continuous parameters of Nature be calculated from theoretical principles, without any input from experiments?"
Consider these two self-referential statements:
“This sentence is true"
“This sentence is false"
These two sentences are axioms -- things declared true by fiat -- and axioms are the basis of reason, which is simply mechanical logical operations on true statements.
As an aside, we know that mechanical operations on self-referential systems can produce "infinite loops":
“The next sentence is true"
“This sentence is false"
Self-referential systems of this form are "undecidable".
But consider these two self-referential statements:
“This sentence has five words"
“This sentence has no words"
The truth or falsity of those statements cannot be ascertained except empirically.
Is Nature self-referential? I suspect that it is (cf. "Searle's Chinese Room Argument". We are self-referential and we are part of Nature. But that raises the question if our self-reference is emergent or fundamental.) Does Nature make statements that can only be decided empirically? Does Nature even speak (i.e. make statements about itself)? That depends on your worldview...
Searle's Chinese Room Argument
[Work in progress... revisions to come]
Searle's "Minds, Brains, and Programs" is an attempt to show that computers cannot think the way humans do and so any effort to create human-level artificial intelligence is doomed to failure. Searle's argument is clearly wrong. What I found most interesting in reading his paper is that Searle's understanding of computers and programs can be shown to be wrong without considering the main part of the argument at all! Of course, it's possible that his main argument is right but that his subsequent commentary is in error but the main mistakes in both will be demonstrated. Then several basic, but dangerous, ideas in his paper will be exposed.
On page 11, Searle presents a dialog where he answers the following five questions (numbers added for convenience for later reference):
1) "Could a machine think?"
The answer is, obviously, yes. We are precisely such machines.
2) "Yes, but could an artifact, a man-made machine think?"
Assuming it is possible to produce artificially a machine with a nervous system, neurons with axons and dendrites, and all the rest of it, sufficiently like ours, again the answer to the question seems to be obviously, yes. If you can exactly duplicate the causes, you could duplicate the effects. And indeed it might be possible to produce consciousness, intentionality, and all the rest of it using some other sorts of chemical principles than those that human beings use. It is, as I said, an empirical question.
3) "OK, but could a digital computer think?"
If by "digital computer" we mean anything at all that has a level of description where it can correctly be described as the instantiation of a computer program, then again the answer is, of course, yes, since we are the instantiations of any number of computer programs, and we can think.
4) "But could something think, understand, and so on solely in virtue of being a computer with the right sort of program? Could instantiating a program, the right program of course, by itself be a sufficient condition of understanding?"
This I think is the right question to ask, though it is usually confused with one or more of the earlier questions, and the answer to it is no.
5) "Why not?"
Because the formal symbol manipulations by themselves don't have any intentionality; they are quite meaningless; they aren't even symbol manipulations, since the symbols don't symbolize anything. In the linguistic jargon, they have only a syntax but no semantics. Such intentionality as computers appear to have is solely in the minds of those who program them and those who use them, those who send in the input and those who interpret the output.
With 1), by saying that we are thinking machines, we introduce the "Church-Turing thesis" which states that if a calculation can be done using pencil and paper by a human, that it can also be done by a Turing machine. If Searle concludes that humans can do something that computers cannot, in theory, do, then he will have deny the C-T thesis and show that what brains do is fundamentally different from what machines do. That brains are different in kind and not in degree.
With 2), Searle runs afoul of computability theory, as brilliantly expressed by Fenynman (Simulating Physics with Computers):
Computer theory has been developed to a point where it realizes that it doesn't make any difference; when you get to a universal computer, it doesn't matter how it's manufactured, how it's actually made.
So 2) doesn't help his argument and, by extension, nor does 3). It doesn't matter if the computer is digital or not (but, see here).
4) is based on a misunderstanding between "computer" and "program". We are so used to creating and running different programs on one piece of hardware that we think that there is some kind of difference between the two. But it's all hardware. Instead of the link to an article I wrote, let me demonstrate this. One of the fundamental aspects of computing is combination and selection. Binary logic is the mechanical selection of one object from two inputs. Consider this way, out of sixteen possible ways, to select one item. Note that it doesn't matter what the objects being selected are. Here we use "x" and "o", but the objects could be bears and bumblebees, or high and low pressure streams of electrons or water.
Table 1 object 1 object 2 result x x o x o x o x x o o x
Clearly, you can't get something from nothing, so the two cases where an object is given as a result when it isn't part of the input requires a bit of engineering. Nevertheless, these devices can be built.
Along with combination and selection another aspect of computation is composition. Let's convert the above table to a device that implements the selection given two inputs in a form that can be composed again and again.
We can arrange these devices so that, regardless of which of the two inputs are given (represented by "✽"), the output is always "x":
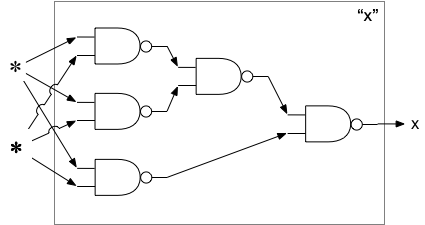
We can also make an arrangement so that the output is always "o", regardless of which inputs are used:

We now have all of the "important"1 aspects of a computer. If we replace "x" with 1 and "o" with 0 then we have all of the computational aspects of a binary computer. Every program is an arrangement of combination and selection operations. If it were economically feasible, we could build a unique network for every program. But the complexity would be overwhelming. One complicating factor is that the above does not support writeable memory. To go from a 0 to a 1 requires another node in the network, plus all of the machine states that can get to that node. For the fun of it, we show how the same logic device that combines two objects according to Table 1 can be wired together to provide memory:
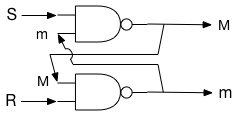
By design, S and R are initially "x", which means M and m are undefined. A continuous stream of "x" is fed into S and R.
Suppose S is set to "o" before resuming the stream of "x". Then:
S = o, M = x, R = x, m = o, S = x, M = x. This shows that when S is set to "o", M becomes "x" and stays "x".
Suppose R is set to "o" before resuming the stream of "x". Then:
R = o, m = x, S = x, M = o, R = x, m = x. This shows that when R is set to "x", M becomes "o" and stays "o", until S is reset to "o".
This shows that every program is a specification of the composition of combination and selection elements. The difference between a "computer" and a "program" is that programs are static forms of the computer: the arrangement of the elements are specified, but the symbols aren't flowing through the network.2 This means that if 1) and 2) are true, then the wiring of the brain is a program, just like each program is a logic network.
Finally, we deal with objection 5). Searle is wrong that there is no "intentionality" in the system. The "intentionality" is the way the symbols flow through the network and how they eventually interact with the external environment. Searle is right that the symbols are meaningless. So how do we get meaning from meaningless? For this, we turn to the Lambda Calculus (also here, and here: part 1, part 2). Meaning is simply a "this is that" relation. The Lambda Calculus shows how data can be associated with symbols. Our brains take in data from our eyes and associate it with a symbol. Our brains take in data from our ears and associate it with another symbol. If what we see is coincident with what we hear, we can add a further association between the "sight" symbol and the "hearing" symbol.3
The problem, then, is not with meaning, but with the ability to distinguish between symbols. The Lambda Calculus assumes this ability. We get meaning out of meaningless symbols because we can distinguish between symbols. Being able to distinguish between things is built into Nature: positive and negative charge is one example.
So Searle's dialog fails, unless you deny the first point and hold that we are not thinking machines. That is, we are something else that thinks. But this denies what we know about brain physiology.
But suppose that Searle disavows his dialog and asks that his thesis be judged solely on his main argument.
Addendum - 01/24/2025
The next update didn't occur until 05/04/20, which is less of an analysis of Searle's paper, but on what another philosopher wrote about Searle's paper. Here, I claimed that meaning is a this is that relation. In my latest take on Searle, a philosopher on X (nee Twitter) took issue with that. The objections that philosophers come up with are bizarre, to say the least. They can go to great lengths to hide that what they are really claiming, namely, that the brain is not Turing compatible. The problem with this is that it is a statement which can neither be proved - nor disproved - by thinking about it. It can only be asserted.[1] This is not meant to make light of all of the remaining hard parts of building a computer. But those details are to support the process of computation: combination, selection, and composition.
[2] One could argue that the steps for evaluating Lambda expressions (substitution, alpha reduction, beta reduction) are the "computer" and that the expressions to be evaluated are the "program". But the steps for evaluating Lambda expressions can be expressed as Lambda expressions. John McCarthy essentially did this with the development of the LISP programming language (here particularly section 4, also here). Given the equivalence of the Lambda Calculus, Turing machines, and implementations of Turing machines using binary logic, the main point stands.
[3] This is why there is no problem with "qualia".
Feser's Philosophy of Mind, #3
consists of purely material or physical objects, processes, and properties, operating according to the same basic physical laws and thereby susceptible of explanation via physical science. There is, in short, no such thing as immaterial substance, or soul, or spirit, nor any aspect of human nature which, in principle, elude explanation in purely physical terms.
I note, purely in passing, that the second sentence doesn't necessarily follow from the first. In any case, Feser then proceeds to argue that it is difficult to see how things like cultural conventions, for example, are:
… hard to reduce to the properties of molecules in motion.
and
There seems to be no way to match up sets of logically interrelated mental states with sets of merely causally interrelated brain states, and thus no way to reduce the mental to the physical.
Here is how it's done. We have no problem understanding that there are quarks and electrons. We have no problem understanding that quarks combine to form protons and neutrons, and that protons, neutrons, and electrons form atoms. Atoms form trees and stars, bacteria and brains.
Instead of combing things into more things, consider the case where two things are "combined" into one of the two things. Consider the physical process where an apple and an apple combine to an orange, and apple and an orange combine to an apple, an orange and an apple combine to an orange, and an orange and an orange combine into an apple. Or consider the case where an apple and an apple combine to orange, while apple and orange, orange and apple, and orange and orange combine to apple. There are sixteen ways for these combinations to happen. We can demonstrate that repeated application of either of two of these processes can reproduce all of the others.
This is a purely physical process. Instead of using apples and oranges, we can use more or fewer electrons flowing through a wire. We can use variable resistors to make a physical process that combines more and fewer electrons just like we combined oranges and apples. Let's call this collection of variable resistors and wires a "device". These devices can be strung together into complex networks.
We can show that arrangements of these devices are equivalent to neurons and computer gates. Furthermore, and this is one of two key insights, arranging devices and wires one way gives one behavior; arranging devices and wires another results in a different behavior.
This is important, because we normally think of a computer as an arrangement of wires and devices that takes a program as input, performs the steps in the program, and produces a result. This leads us to believe that a computer cannot do anything without programming. Feser falls into this way of thinking when he writes:
A computer program is something abstract – a mathematical structure that can be understood and specified, on paper or in the programmer’s mind, long before anyone implements it in a machine.
While this isn't wrong, it hides the key concept that the arrangement of the wires and devices is the program. No external program is necessary. If it were cost effective, instead of writing abstract programs that run on a general purpose computer, we could custom build an arrangement of wires and devices for each program we wished to run.
Once we understand that the physical network itself is the program, we have to ask how we can get meaning out of networks of apples and oranges or high and low voltages. Consider the network that given an apple and an apple, or an orange and an orange, produces an apple and when given an apple and an orange or an orange and an apple produces an orange. This is equivalent to the question "are the inputs equal" with "apple" being assumed to be "yes". We could just as easily chose the network that takes apple and apple or orange and orange and outputs orange. The choice of which network to use is completely arbitrary, but networks that use this convention can now be constructed that can compare two things for equality. This is the second key insight. Meaning is achieved by building a network that uses one of the two inputs to answer the question "are these things equal?" And once you have that, you have the basis for constructing systems that can, for example, associate sights with sounds.
One network can wag a tail at the enjoyment of a bone, another network can contemplate the ontology of thought. Dogs don't discuss epistemology simply because their brain wiring is insufficient for the task.
So the question isn't "is thought a physical process?" It certainly is. Logic is built into the very fabric of reality. The "devices" are just logic gates. The astounding thing is that a network of these gates can recognize and describe themselves. Furthermore, our brains aren't capable of proving that logic can be separated from reality. Every attempt to do so changes reality such that we destroy our ability to think.
The real question is "how did these complex networks arise in the first place?" But with the current state of the art, the answer to that question depends very much on your philosophical assumptions.
Feser's Philosophy of Mind, #2
Feser ends chapter one by introducing the "mind-body" problem which is this: if the brain is purely physical, how can something that is composed of atoms think and be conscious of itself and its surroundings? Are mind and "matter" two fundamentally different kinds of things ("dualism") or are mind and matter different forms of the same thing? In chapter 2, Feser presents three arguments for dualism, and one argument against it. The three positive arguments are the "indivisibility," "obviousness," and "conceivability" arguments, while the "interaction" argument is the negative argument. I will not consider the interaction argument here.
The indivisibility argument goes like this. Matter is one form of substance which can be divided into parts. Atoms can be divided into protons, neutrons, and electrons; protons and neutrons can be divided into quarks; quarks and electrons are made up of strings (assuming string theory is true), with the string being the fundamental indivisible unit of matter. What remains after each division is of the same kind — it's matter all the way down — and since it doesn't divide into something else, it's one "substance". A mind, however, is not divisible. The "I" is one (considerations of schizophrenia not withstanding). Therefore, the "string" and the "mind" are two fundamentally different things.
A problem with this is that "matter" is not the only component to the physical universe. Along with strings (or higher level particles), there is space-time, motion, energy, charge, etc… To hold to dualism is to say that mind is not only not any of these things, but is also not some form of combination of these things. If mind is some form of combination of these things, then the "indivisibility" of the mind might only hold when the combination of these things are working in concert. Break the synchronization of the parts and the mind ceases to function correctly (or at all).
The obviousness argument holds that just as oranges and apples are obviously different, mind and matter are obviously different. That is, because we perceive them differently, they are fundamentally different. Oranges and apples have different shapes, textures, colors, and tastes. But the indivisibility argument shows that apples and oranges aren't fundamentally different. They are just different arrangements of the number and kinds of atoms, which are just different arrangements of electrons and quarks. The dualist's perceived difference between mind and brain, like the difference between apples and oranges, could be explained by the operation of nature where the mechanism isn't immediately obvious. Someone who has never seen a modern phone might wonder at a symphony coming from someone's pocket. Humans are not violins and to hear the Brandenburg Concerto #3 coming from someone's pocket might cause no end of consternation and speculation as to its cause. Saying that mental stuff is different from physical stuff is to put a label on a lack of knowledge and put it in its own category.
The conceivability argument is as follows:
That is to say, it is entirely conceivable that one could exist as a disembodied mind, with one’s body and brain, and indeed the entire physical world, being nothing but a figment of one’s imagination. But then it is conceivable and therefore at least metaphysically possible for the mind to exist apart from the brain. Therefore, the mind is not identical to the brain.
The problems with this are manifold. First, the mind is not identical to the brain, any more than a symphony is identical to an orchestra. Therefore, this doesn't show that the mind can exist apart from the brain. Second, the conceivability argument can be used to show that solipsism is true. But in chapter 1, Feser argues against solipsism, thereby undercutting the power of the conceivability argument. Third, Feser himself admits the weakness of conceivability arguments in the next chapter by writing:
But conceivability arguments, if they prove anything…
Conceivability arguments prove nothing at all.
The indivisibility, obviousness, and conceivability arguments are so bad that professors who present them should be stripped of their degrees and run out of their supporting institutions.
And I say this as a convinced dualist1. But I am a dualist who thinks that matter and mind are so entangled in a loop that they are impossible to separate without destroying our ability to think about them (cf. The Physical Nature of Thought).
[1] I am no longer a convinced dualist. I haven't rejected it altogether, but I also haven't finished thinking about my counterargument.
Feser's Philosophy of Mind, #1
There are several problems with this argument. First, Occam's Razor is a heuristic. It is simply a guideline, a good guess, when choosing between alternatives. But anyone familiar with search techniques in artificial intelligence knows that even good guesses can ultimately lead to less than optimal or even wrong conclusions. If you don't end up in a dead end, there might still be an untried path to a more favorable outcome.
Second, and more importantly, Occam's Razor only applies when all other considerations are equal. That is, Occam's Razor should be used only when both systems give the same independently verifiable answer to the same questions. Both the Ptolemaic and Copernican systems predict the same positions of the planets in the night sky. But the Copernican system is simpler and so is justified by Occam's Razor. So the use of Occam's Razor is therefore not applicable in this case, because the answers to the same questions can be wildly different in the Realist and Solipsist systems.
Third, we can't really tell which system is simpler. Since we don't ultimately know what reality really is, any argument that the implementation of reality in one form is simpler than the implementation of reality in another is dubious, at best. No one has any idea what it takes to implement the reality that appears to be external to us, any more than we have any idea that we know what it takes to implement a mind that thinks there is an external reality.
Fourth, if a system with an entity which manipulates our minds is more complex than an external reality, then Feser has justified disbelief in Theism in general, and Christianity in particular, since God is one more complicating factor in an already complex system. Given that Feser is a theist, he may want to reconsider this use of the razor.
So Occam's Razor fails as a means to justify realism over solipsism. Granted, Feser conditions this justification with “If all this is right…" but, still, an inauspicious start to this book. The correct answer is that we choose one or the other simply because we choose one over the other. Post hoc rationalizations as to why we made a particular choice will vary depending on which system we chose.
The Halting Problem and Human Behavior
It is obvious that the function
(defun P1 ()will return the string "Hello, World!" and halt.
"Hello, World!")
It is also obvious that the function
(defun P2 ()never halts. Or is it obvious? Depending on how the program is translated, it might eventually run out of stack space and crash. But, for ease of exposition, we'll ignore this kind of detail, and put P2 in the "won't halt" column.
(P2))
What about this function?
(defun P3 (n)Whether or not, for all N greater than 1, this sequence converges to 1 is an unsolved problem in mathematics (see The Collatz Conjecture). It's trivial to test the sequence for many values of N. We know that it converges to 1 for N up to 1,000,000,000 (actually, higher, but one billion is a nice number). So part of the test for whether or not P3 halts might be:
(when (> n 1)
(if (evenp n)
(P3 (/ n 2))
(P3 (+ (* 3 n) 1)))))
(defun halt? (Pn Pin)But what about values greater than one billion? We can't run a test case because it might not stop and so halt? would never return.
…
(if (and (is-program Pn collatz-function) (<= 1 Pin 1000000000))
t
…)
We can show that a general algorithm to determine whether or not any arbitrary function halts does not exist using an easy proof.
Suppose that halt? exists. Now create this function:
(defun snafu ()If halt? says that snafu halts, then snafu will loop forever. If halt? says that snafu will loop, snafu will halt. This shows that the function halt? can't exist when knowledge is symmetrical.
(if (halt? snafu nil)
(snafu)))
As discussed here, Douglas Hofstadter, in Gödel, Escher, Bach, wrote:
It is an inherent property of intelligence that it can jump out of the task which it is performing, and survey what it is done; it is always looking for, and often finding, patterns. (pg. 37)
Over 400 pages later, he repeats this idea:
This drive to jump out of the system is a pervasive one, and lies behind all progress and art, music, and other human endeavors. It also lies behind such trivial undertakings as the making of radio and television commercials. (pg. 478).
This behavior can be seen in looking at the halting problem. After all, one is tempted to say, "Wait a minute. What if I take the environment in which halt? is called into account? halt? could say, 'when I'm analyzing a program and I see it trying to use me to change the outcome of my prediction, I'll return that the program will halt, but when I'm running as a part of snafu, I'll return true. That way, when snafu is running, it will then halt and so the analysis will agree with the execution.' We have "jumped out of the system" and made use of information not available to snafu, and solved the problem.
Except that we haven't. The moment we formally extend the definition of halt? to include the environment, then snafu can make use of it to thwart halt?
(defun snafu-extended ()We can say that our brains view halt? and snafu as two systems that compete against each other: halt? to determine the behavior of snafu and snafu to thwart halt?. If halt? can gain information about snafu, that snafu does not know, then halt? can get the upper hand. But if snafu knows what halt? knows, snafu can get the upper hand. At what point do we say, "this is madness?" and attempt to cooperate with each other?
(if (halt? snafu-extended nil 'running)
(snafu-extended)))
I am reminded of the words of St. Paul:
Knowledge puffs up, but love builds up. — 1 Cor 8:1b
The Physical Nature of Thought
Two monks were arguing about a flag. One said, "The flag is moving." The other said, "The wind is moving." The sixth patriarch, Zeno, happened to be passing by. He told them, "Not the wind, not the flag; mind is moving."
-- "Gödel, Escher, Bach", Douglas Hofstadter, pg. 30
Is thought material or immaterial? By "material" I mean an observable part of the universe such as matter, energy, space, charge, motion, time, etc... By "immaterial" would be meant something other than these things.
Russell wrote:
The problem with which we are now concerned is a very old one, since it was brought into philosophy by Plato. Plato's 'theory of ideas' is an attempt to solve this very problem, and in my opinion it is one of the most successful attempts hitherto made. … Thus Plato is led to a supra-sensible world, more real than the common world of sense, the unchangeable world of ideas, which alone gives to the world of sense whatever pale reflection of reality may belong to it. The truly real world, for Plato, is the world of ideas; for whatever we may attempt to say about things in the world of sense, we can only succeed in saying that they participate in such and such ideas, which, therefore, constitute all their character. Hence it is easy to pass on into a mysticism. We may hope, in a mystic illumination, to see the ideas as we see objects of sense; and we may imagine that the ideas exist in heaven. These mystical developments are very natural, but the basis of the theory is in logic, and it is as based in logic that we have to consider it. [It] is neither in space nor in time, neither material nor mental; yet it is something. [Chapter 9]
I claim that Russell and Plato are wrong. Not necessarily that ideas exist independently from the material. They might.1 Rather, I claim that if ideas do exist apart from the physical universe, then we can't prove that this is the case. The following is a bare minimum outline of why.
Logic
Logic deals with the combination of separate objects. Consider the case of boolean logic. There are sixteen way to combine apples and oranges, such that two input objects result in one output object. These sixteen possible combinations are enumerated here. The table uses 1's and 0's instead of apples and oranges, but that doesn't matter. It could just as well be bees and bears. For now, the form of the matter doesn't matter. What's important is the outputs associated with the inputs2.Composition
Suppose, for the sake of argument, that we have 16 devices that combine things according to each of the 16 possible ways to combine two things into one. We can compose a sequence of those devices where the output of one device becomes the input to another device. We first observe that we don't really need 16 different devices. If we can somehow change an "orange" into an "apple" (or 1 into 0, or a bee into a bear) and vice versa, then we only need 8 devices. Half of them are the same as the other half, with the additional step of "flipping" the output. With a bit more work, we can show that two of the sixteen devices when chained can produce the same output as any of the sixteen devices. These two devices, known as "NOT OR" (or NOR) and "NOT AND" (or NAND) are called "universal" logic devices because of this property. So if we have one device, say a NAND gate, we can do all of the operations associated with Boolean logic.3Calculation
NAND devices (henceforth called gates) are a basis for modern computers. The composition of NAND gates can perform addition, subtraction, multiplication, division, and so on. As an example, the previously referenced page concluded by using NAND gates to build a circuit that added binary numbers. This circuit was further simplified here and then here.Memory
We further observe that by connecting two NAND gates a certain way that we can implement memory.Computation
Memory and calculation, all of which are implemented by arrangements of NAND gates, are sufficient to compute anything which can be computed (cf. Turing machines and the Church-Turing thesis).Meaning
Electrons flowing through NAND gates don't mean anything. It's just the combination and recombination of high and low voltages. How can it mean anything? Meaning arises out of the way the circuits are wired together. Consider a simple circuit that takes two inputs, A and/or B. If both inputs are A it outputs A, if both inputs are B then it outputs A, and if one input is A and the other is B, it outputs B. By making the arbitrary choice that "A" represents "yes" or "true" or "equal", more complex circuits can be built that determine the equivalence of two things. This is the simplified version of Hofstadter's claim:
When a system of "meaningless" symbols has patterns in it that accurately track, or mirror, various phenomena in the world, then that tracking or mirroring imbues the symbols with some degree of meaning -- indeed, such tracking or mirroring is no less and no more than what meaning is.
-- Gödel, Escher, Bach; pg P-3
Neurons and NAND gates
The brain is a collection of neurons and axons through which electrons flow. A computer is a collection of NAND gates and wires through which electrons flow. The differences are the number of neurons compared to the number of NAND gates, the number and arrangement of wires, and the underlying substrate. One is based on carbon, the other on silicon. But the substrate doesn't matter.That neurons and NAND gates are functionally equivalent isn't hard to demonstrate. Neurons can be arranged so that they perform the same logical operation as a NAND gate. A neuron acts by summing weighted inputs, comparing to a threshold, and "firing" if the weighted sum is greater than the threshold. It's a calculation that can be done by a circuit of NAND gates.
Logic, Matter, and Waves
It's possible to create logic gates using particles. See, for example, the Billiard-ball computer, or fluid-based gates where particles (whether billiard balls or streams of water) bounce off each other such that the way they bounce can implement a universal gate.It's also possible to create logic gates using waves. See, for example, here [PDF] and here [paid access] for gates using acoustics and optics.
I suspect, but need to research further, that waves are the proper way to model logic, since it seems more natural to me that the combination of bees and bears is a subset of wave interference rather than particle deflection.
Self-Reference
 4 So why are Russell and Plato wrong? It is because it is the logic gates in our brains that recognize logic, i.e. the way physical things combine. Just as a sequence of NAND gates can output "A" if the inputs are both A or both B; a sequence of NAND gates can recognize itself. Change a wire and the ability to recognize the self goes away. That's why dogs don't discuss Plato. Their brains aren't wired for it. Change the wiring in our brains and we wouldn't, either. Hence, while we can separate ideas from matter in our heads, it is only because of a particular arrangement of matter in our heads. There's no way for us to break this "vicious" circle.
4 So why are Russell and Plato wrong? It is because it is the logic gates in our brains that recognize logic, i.e. the way physical things combine. Just as a sequence of NAND gates can output "A" if the inputs are both A or both B; a sequence of NAND gates can recognize itself. Change a wire and the ability to recognize the self goes away. That's why dogs don't discuss Plato. Their brains aren't wired for it. Change the wiring in our brains and we wouldn't, either. Hence, while we can separate ideas from matter in our heads, it is only because of a particular arrangement of matter in our heads. There's no way for us to break this "vicious" circle.Footnotes
[1] "In the beginning was the Word..." As a Christian, I take it on faith that the immaterial, transcendent, uncreated God created the physical universe.[2] Note that the "laws of logic" follow from the world of oranges and apples, bees and bears, 1s and 0s. Something is either an orange or an apple, a bee or a bear. Thus the "law" of contradiction. An apple is an apple, a zero is a zero. Thus the "law" of identity. Since there are only two things in the system, the law of the excluded middle follows.
[3] This previous post shows how NAND gates can be composed to calculate all sixteen possible ways to combine two things.
[4] "Drawing Hands", M. C. Escher
The "Problem" of Qualia
[updated 25 July 2022 to provide more detail on "Blind Mary"]
[updated 5 August 2022 to provide reference to Nobel Prize for research into touch and heat; note that movie Ex Machina puts the "Blind Mary" experiment to film]
[updated 6 January 2024 to say more about philosophical zombies]
[updated 4 November 2024 to expand on "Blind Mary"]
"Qualia" is the term given to our subjective sense impressions of the world. How I see the color green might not be how you see the color green, for example. From this follows flawed arguments which try to show how qualia are supposedly a problem for a "physicalist" explanation of the world.
The following diagram shows an idealized process by which different colors of light enter the eye and are converted into "qualia" -- the brain's internal representation of the information. Obviously the brain doesn't represent color as 10 bits of information. But the principle remains the same, even if the actual engineering is more complex.
Read More...
Gems from John R. Pierce

"Mathematically, white Gaussian noise, which contains all frequencies equally, is the epitome of the various and unexpected. It is the least predictable, the most original of sounds. To a human being, however, all white Gaussian noise sounds alike. It's subtleties are hidden from him, and he says that it is dull and monotonous. If a human being finds monotonous that which is mathematically most various and unpredictable, what does he find fresh and interesting? To be able to call a thing new, he must be able to distinguish it from that which is old. To be distinguishable, sounds must be to a degree familiar. … We can be surprised repeatedly only by contrast with that which is familiar, not by chaos." [pg. 251, 267]
Christianity and Computer Science
But what to study? My standard response these days is either theology or computer science. Then I add that I'm not sure that I really see a difference between the two. While driving in to work this morning, my subconscious found that my flippancy isn't so far off the mark. If thought is matter in motion in certain patterns (which it is), then writing software is the act of putting thought in physical form. A moment's reflection shows that this must be so: the computer is all hardware. The software is just ones and zeros but, again, this is just a collection of physical states arranged in specific ways. If the criticism is that "computers don't think!", the answer is that this is because computers don't have the huge number of connections that are in the human brain. But in time they will.
Putting thought in physical form is what God did with His Son. "In the beginning was the Word, and the Word was with God, and the Word was God. … And the Word became flesh and dwelt among us." Jesus is God's thoughts in physical form.
So Christianity and computer science are both incarnational.
Modeling the Brain
The "autonomous" section is concerned with the functions of the brain that operate apart from conscious awareness or control. It will receive no more mention.
The "introspection" division monitors the goal processing portion. It is able to monitor and describe what the goal processing section is doing. The ability to introspect the goal processing unit is what gives us our "knowledge of good and evil." See What Really Happened In Eden, which builds on The Mechanism of Morality. I find it interesting that recent studies in neuroscience show:
But here is where things get interesting. The subjects were not necessarily consciously aware of their decision until they were about to move, but the cortex showing they were planning to move became activated a full 7 seconds prior to the movement. This supports prior research that suggests there is an unconscious phase of decision-making. In fact many decisions may be made subconsciously and then presented to the conscious bits of our brains. To us it seems as if we made the decision, but the decision was really made for us subconsciously.
The goal processing division is divided into two opposing parts. In order to survive, our biology demands that we reproduce, and reproduction requires food and shelter, among other things. We generally make choices that allow our biology to function. So part of our brain is concerned with selecting and achieving goals. But the other part of our brain is based on McCarthy's insight that one of the requirements for a human-level artificial intelligence is that "All aspects of behavior except the most routine should be improvable. In particular, the improving mechanism should be improvable." I suspect McCarthy was thinking along the lines of Getting Computers to Learn. However, I think it goes far beyond this and explains much about the human mind. In particular, introspection of the drive to improve leads to the idea that nothing is what it ought to be and gives rise to the is-ought problem. If one part of the goal processing unit is focused on achieving goals, this part is concerned with focused on creating new goals. As the arrows in the diagram show, if one unit focuses toward specific goals, the other unit focuses away from specific goals. Note that no two brains are the same -- individuals have different wiring. In some, the goal fixation process will be stronger; in other, the goal creation process will be stronger. One leads to the dreamer, the other leads to the drudge. Our minds are in dynamic tension.
Note that the goal formation portion of our brains, the unit that wants to "jump outside the system" is a necessary component of our intelligence.
On The Difference Between Hardware and Software
The No Free Will Theorem
Earlier this week, over at Vox Popoli, Vox took issue with a particular scientific study that concluded on the basis of experimental data that free will does not exist. While I think I agree that this study does not show what it claims to show, I nevertheless took the approach the free will doesn't exist. The outline of a proof goes like this.
Either thought follows the laws of physics, or it does not. X or ~X. I hold the law of non-contradiction to be true. Now, someone might quibble about percentages: most of the time our thoughts follow the laws of physics, but sometimes they do not. But that misses the point.
Why would anyone suppose that our thoughts don't follow the laws of physics? Perhaps because of an idea that thought is "mystical" stuff; that there is a bit of "god stuff" in our heads that gives us the capabilities that we have. If this were so, since the Christian God transcends nature, our thoughts would transcend nature. It's how we would avoid non-existence upon physical death: the "soul" which is made of "god stuff" returns to God. Perhaps it's due to not knowing how thinking is accomplished in the brain. What I'm about to say certainly isn't taught in any Sunday school I've ever attended, or been discussed in any theological book I've ever read. While that may be because I don't get out enough, I suspect my experience isn't atypical. Another, more general reason, is because that's the way our brains perceive how they operate. It's the "default setting," as it were. Most people, regardless of upbringing, think they have free will. I think I can explain why it's that way, but that's for another post.
How does one prove that thoughts follow the laws of physics? The ultimate test would be to build a human level artificial intelligence. I can't do that. The technology isn't there. Yet. The best I can do is offer a proof of concept. I maintain that this is better than what the proponent of mystical thought can do. I know of no way to build something that doesn't obey the laws of physics. By definition, we can't do it. So any proof would have to come form some source from outside nature held to be authoritative. In my world, that's typically the Bible. There is no end of Bible scholars who hold that Scripture teaches that man has free will. It doesn't, but my intent here is to make may case, not refute their arguments. Although I acknowledge that it certainly wouldn't hurt to do so elsewhere.
What is thought? Thought is matter in motion in certain patterns. This is a key insight which must be grasped. The matter could be photons, it could be water; in our brain it is electrons. The pattern of the flow of electrons is controlled by the neurons in our brain, just like the pattern of the flow of electrons is controlled by NAND gates in a computer. While neurons and NAND gates are different in practice, they are not different in principle. NAND gates can simulate neurons (there are, after all, computer programs that do this) and neurons can simulate NAND gates (cf. here). Another way to view this is that every time a programmer writes computer software, they are embedding thought into matter. I've been programming professionally for almost 40 years and it wasn't until recently that I understood this obvious truth. But if this is so, why aren't there intelligent computers? As I understand it, there are some 100 billion neurons in the brain with some 5 trillion connections. Computers have not yet achieved that level of complexity. Can they? How many NAND gates will it take to achieve the equivalent functionality of 5 trillion neuron connections? I don't know. But the principle is sound, even if the engineering escapes us.
Humans are governed by the laws of quantum mechanics, just as computers are. Having just re-watched all four seasons of Battlestar Galactica on Netflix, it was fascinating to watch the denial of some humans that machines could be their equal, and the denial of some machines that they could be human. In the season 4 episode No Exit, the machine's complaint to his creator "why did you make me like this," is straight out of Romans 9. Art, great art, imitating life.
However one cares to define the concept of "free will," that definition must apply to computers as equally as it does to man. The same principles govern both. As long as it meets that criteria, I can live with silly notions of what "free" means. "You are free to wander around inside this fenced area, but you can't go outside" is usually how the definitions end up. I think limited freedom is an oxymoron, but people want to cling to their illusions.
There is so much more to cover. If our thoughts are the movement of electrons in certain patterns, then how is that motion influenced? What are the feedback loops in the brain? What is the effect of internal stimuli and external stimuli? Is one greater than the other? The Bible exhorts the Christian to place themselves where external stimuli promotes the faith. The dances of their electrons can influence the dance of our electrons. Can we make Christians (or Democrats, or Atheists, or…) through internal modification of brain structures through drugs or surgery? How does God change the path of electrons in those who believe versus those who don't? Would God save an intelligent machine? Could they be "born again"? Does God hide behind quantum indeterminacy? So many questions.
In April 2009, I wrote the post Ecclesiastes and the Sovereignty of God, which gave excepts from the book A Time to Be Born - A Time to Die, by Robert L. Short. Using the Bible, in particular the book of Ecclesiastes, Short reaches the same conclusion I do arguing from basic physics.
The universe controls us. We do not control the universe.
This brings me to the Gene Wolfe quote mentioned at the beginning of this post:
This is what mankind has always wanted. … That the environment should respond to human thought. That is the core of magic and the oldest dream of mankind…. when humankind has dreamed of magic, the wish behind the dream has been the omnipotence of thought.
[to be continued]
On the Inadequacy of Scientific Knowledge
If true, that rule is not a minor flaw in scientific reasoning. The law is completely nihilistic. It is a catastrophic logical disproof of the general validity of all scientific method!
If the purpose of scientific method is to select from a multitude of hypothesis, and if the number of hypothesis grows faster than the experimental method can handle, then it is clear that all hypothesis can never be tested. If all hypothesis cannot be tested, then the results of any experiment are inconclusive and the entire scientific method falls short of its goal of establishing proven knowledge.
About this Einstein had said, "Evolution has shown that at any given moment out of all conceivable constructions a single one has proved absolutely superior to all the rest," and let it go at that. But to Phaedrus3 that was an incredibly weak answer. The phrase "at any given moment" really shook him. Did Einstein really mean to state that truth was a function of time? To state that would annihilate the most basic presumption of all science!
But there it was, the whole of history of science, a clear story of continuously new and changing explanations of old facts. The time spans of permanence seemed completely random, he could see no order to them. Some scientific truths seemed to last for centuries, others for less than a year. Scientific truth was not a dogma, good for eternity, but a temporal quantitative entity that could be studied like anything else.
He studied scientific truths, then became upset even more by the apparent cause of their temporal condition. It looked as though the time spans of scientific truths are an inverse function of the intensity of scientific effort. Thus the scientific truths of the twentieth century seem to have a much shorter life-span than those of the last century because scientific activity is now much greater. If, in the next century, scientific activity increases tenfold, then the life expectancy of any scientific truth can be expected to drop to perhaps one-tenth as long as now. What shortens the lifespan of the existing truth is the volume of hypothesis offered to replace it; the more the hypothesis, the shorter the time span of the truth. And what seems to be causing the number of hypothesis to grow in recent decades seems to be nothing other than scientific method itself. The more you look, the more you see. Instead of selecting one truth from a multitude, you are increasing the multitude. What this means logically is that as you try to move toward unchanging truth through the application of scientific method, you actually do not move toward it at all. You move away from it. It is your application of scientific method that that is causing it to change!
What Phaedrus observed on a personal level was the phenomenon, profoundly characteristic of the history of science, which has been swept under the carpet for years. The predicted results of scientific enquiry and the actual results of scientific enquiry are diametrically opposed here, and no one seems to pay much attention to the fact. The purpose of scientific method is to select a single truth from among many hypothetical truths. That, more than anything else, is what science is all about. But historically science has done exactly the opposite. Through multiplication upon multiplication of facts, information, theories, and hypotheses, it is science itself that is leading mankind from single absolute truths to multiple, indeterminate, relative ones. The major producer of the social chaos, the indeterminacy of thought and values that rational knowledge is supposed to eliminate, is none other than science itself. And what Phaedrus saw in the isolation of his own laboratory work is now seen everywhere in the technological world today. Scientifically produced antiscience -- chaos.
There is a lot to consider and commend in this argument. Certainly, anyone who has uttered, "the more I know the less I know" understands that as knowledge increases the unknown also appears to increase. Every advance in knowledge pushes out the unexplored frontier. It is unclear how much there is to be known. Even if an argument to the boundedness of knowledge about the physical universe could be made based upon the number of particles therein, I suspect we will find limits to how far we can explore. We likely cannot know all that could be known. And this omits the field of mathematical knowledge, where Gödel showed the incompleteness of formal systems.
The idea that scientific knowledge is a function of time needs to be stressed. Now I happen to think4 that the recent Opera claim of superluminal neutrinos won't stand upon further investigation, but if it does it will require adjustments to relativity.
Finally, if it is true that science produces antiscience then the resulting chaos can't be repaired by more application of the scientific method, unless scientific knowledge is finite.
While I think that much of this argument has merit, I put it in the Bad Arguments category, not because I necessarily disagree with the conclusions, but because the premise that "the purpose of the scientific method is to select a single truth from many hypothetical truths" is wrong. The scientific method is not "when I repeatedly do this I get that result therefore this result can always be expected". That's observation and induction, no different from "the sun rose yesterday, the sun rose today, therefore the sun will rise tomorrow." We know there will come a time when the sun won't rise the next day. Induction is not a sure means to truth, even though we often have to rely on it.5 As Einstein said, "No amount of experimentation can ever prove me right; a single experiment can prove me wrong."6
The power of the scientific method comes from the logical equation: (A → B) ∧ ¬B → ¬A. In English, "if A implies B, and B is not true, then A is not true." Experiments don't establish theories, they show if a theory is wrong. The scientific method doesn't establish truth, it establishes falsehood. Consider a piece of paper as an analogy to knowledge. Let the color gray represent what we don't know. Let white represent truth. Let black stand for falsehood. The paper starts out gray. We don't know if the paper is finite or infinite in extent. Science can turn gray areas black, to represent the things we know are not true. But it can't turn gray areas white.
And yet, the earth revolves around the sun and E=mc2. Even if superluminal neutrinos really do exist, atomic weapons still work by turning a little bit of matter into a lot of energy. How we go from gray to white is another topic for another day. But with the correction of Pirsig's premise, much of his argument still follows.
[1] In the Author's Note, Pirsig writes "[this book] should in no way be associated with that great body of factual information relating to orthodox Zen Buddhist practice. It's not very factual on motorcycles either."
[2] Pg. 559. I don't know why I bother with page numbers, as they vary from e-reader to e-reader.
[3] Phaedrus is the author in an earlier stage of his life.
[4] I'm no expert. Don't wager based on my opinion.
[5] See On Induction by Russell.
[6] This appears to be a paraphrase. See here.
Atheism and Evidence, Redux
Today, I came across the article "Does Secularism Make People More Ethical?" The main thesis of the article is nonsense, but it does reference work by Catherine Caldwell-Harris of Boston University. Der Spiegel (The Mirror) said:
Boston University's Catherine Caldwell-Harris is researching the differences between the secular and religious minds. "Humans have two cognitive styles," the psychologist says. "One type finds deeper meaning in everything; even bad weather can be framed as fate. The other type is neurologically predisposed to be skeptical, and they don't put much weight in beliefs and agency detection."
Caldwell-Harris is currently testing her hypothesis through simple experiments. Test subjects watch a film in which triangles move about. One group experiences the film as a humanized drama, in which the larger triangles are attacking the smaller ones. The other group describes the scene mechanically, simply stating the manner in which the geometric shapes are moving. Those who do not anthropomorphize the triangles, she suspects, are unlikely to ascribe much importance to beliefs. "There have always been two cognitive comfort zones," she says, "but skeptics used to keep quiet in order to stay out of trouble."
This broadly agrees with the Scientific American article, although it isn't clear if the non-anthropomorphizing group is thinking teleologically, but then suppressing it (which is characteristic of atheists) or not seeing meaning at all (characteristic of those with Asperger's).
Caldwell-Harris' work buttresses the thesis of Atheism: It isn't about evidence.
Too, her work is interesting from a perspective in artificial intelligence. One purpose of the Turing Test is to determine whether or not an artificial intelligence has achieved human-level capability. Her "triangle film" isn't dissimilar from a form of Turing Test since agency detection is a component of recognizing intelligence. If the movement of the triangles was truly random, then the non-anthropomorphizing group was correct in giving a mechanical interpretation to the scene. But if the filmmaker imbued the triangle film with meaning, then the anthropomorphizing group picked up a sign of intelligent agency which was missed by the other group.
I wrote her and asked about this. She has absolutely no reason to respond to my query, but I hope she will.
Finally, I have to mention that the Der Spiegel article cites researchers that claim that secularism will become the majority view in the west, which contradicts the sources in my blog post. On the one hand, it's a critical component of my argument. On the other hand, I just don't have time for more research into this right now.
McCarthy, Hofstadter, Hume, AI, Zen, Christianity
For example, in Gödel, Escher, Bach, Hofstadter writes:
It is an inherent property of intelligence that it can jump out of the task which it is performing, and survey what it is done; it is always looking for, and often finding, patterns. (pg. 37)
Over 400 pages later, he repeats this idea:
This drive to jump out of the system is a pervasive one, and lies behind all progress and art, music, and other human endeavors. It also lies behind such trivial undertakings as the making of radio and television commercials. (pg. 478).
It seems to me that McCarthy's third requirement is behind this drive to "jump out" of the system. If a system is to be improved, it must be analyzed and compared with other systems, and this requires looking at a system from the outside.
Hofstadter then ties this in with Zen:
In Zen, too, we can see this preoccupation with the concept of transcending the system. For instance, the kōan in which Tōzan tells his monks that "the higher Buddhism is not Buddha". Perhaps, self transcendence is even the central theme of Zen. A Zen person is always trying to understand more deeply what he is, by stepping more and more out of what he sees himself to be, by breaking every rule and convention which he perceives himself to be chained by – needless to say, including those of Zen itself. Somewhere along this elusive path may come enlightenment. In any case (as I see it), the hope is that by gradually deepening one's self-awareness, by gradually widening the scope of "the system", one will in the end come to a feeling of being at one with the entire universe. (pg. 479)
Note the parallels to, and differences with, Christianity. Jesus said to Nicodemus, "You must be born again." (John 3:3) The Greek includes the idea of being born "from above" and "from above" is how the NRSV translates it, even though Nicodemus responds as if he heard "again". In either case, you must transcend the system. The Zen practice of "breaking every rule and convention" is no different from St. Paul's charge that we are all lawbreakers (Rom 3:9-10,23). The reason we are lawbreakers is because the law is not what it ought to be. And it is not what it ought to be because of our inherent knowledge of good and evil which, if McCarthy is right, is how our brains are wired. Where Zen and Christianity disagree is that Zen holds that man can transcend the system by his own effort while Christianity says that man's effort is futile: God must affect that change. In Zen, you can break outside the system; in Christianity, you must be lifted out.
Note, too, that both have the same end goal, where finally man is at "rest". The desire to "step out" of the system, to continue to "improve", is finally at an end. The "is-ought" gap is forever closed. The Zen master is "at one with the entire universe" while for the Christian, the New Jerusalem has descended to Earth, the "sea of glass" that separates heaven and earth is no more (Rev 4:6, 21:1) so that "God may be all in all." (1 Cor 15:28). Our restless goal-seeking brain is finally at rest; the search is over.
All of this as a consequence of one simple design requirement: that everything must be improvable.
The Is-Ought Problem Considered As A Question Of Artificial Intelligence
In every system of morality, which I have hitherto met with, I have always remarked, that the author proceeds for some time in the ordinary way of reasoning, and establishes the being of a God, or makes observations concerning human affairs; when of a sudden I am surprized to find, that instead of the usual copulations of propositions, is, and is not, I meet with no proposition that is not connected with an ought, or an ought not. This change is imperceptible; but is, however, of the last consequence. For as this ought, or ought not, expresses some new relation or affirmation, it is necessary that it should be observed and explained; and at the same time that a reason should be given, for what seems altogether inconceivable, how this new relation can be a deduction from others, which are entirely different from it.
This is the "is-ought" problem: in the area of morality, how to derive what ought to be from what is. Note that it is the domain of morality that seems to be the cause of the problem; after all, we derive ought from is in other domains without difficulty. Artificial intelligence research can show why the problem exists in one field but not others.
The is-ought problem is related to goal attainment. We return to the game of Tic-Tac-Toe as used in the post The Mechanism of Morality. It is a simple game, with a well-defined initial state and a small enough state space that the game can be fully analyzed. Suppose we wish to program a computer to play this game. There are several possible goal states:
- The computer will always try to win.
- The computer will always try to lose.
- The computer will play randomly.
- The computer will choose between winning or losing based upon the strength of the opponent. The more games the opponent has won, the more the computer plays to win.
As another example, suppose we wish to drive from point A to point B. The final goal is well established but there are likely many different paths between A and B. Additional considerations, such as shortest driving time, the most scenic route, the location of a favorite restaurant for lunch, and so on influence which of the several paths is chosen.
Therefore, we can characterize the is-ought problem as a beginning state B, an end state E, a set P of paths from B to E, and a set of conditions C. Then "ought" is the path in P that satisfies the constraints in C. Therefore, the is-ought problem is a search problem.
The game of Tic-Tac-Toe is simple enough that the game can be fully analyzed - the state space is small enough that an exhaustive search can be made of all possible moves. Games such as Chess and Go are so complex that they haven't been fully analyzed so we have to make educated guesses about the set of paths to the end game. The fancy name for these guesses is "heuristics" and one aspect of the field of artificial intelligence is discovering which guesses work well for various problems. The sheer size of the state space contributes to the difficulty of establishing common paths. Assume three chess programs, White1, White2, and Black. White1 plays Black, and White2 plays Black. Because of different heuristics, White1 and White2 would agree on everything except perhaps the next move that ought to be made. If White1 and White2 achieve the same won/loss record against Black; the only way to know which game had the better heuristic would be to play White1 against White2. Yet even if a clear winner was established, there would still be the possibility of an even better player waiting to be discovered. The sheer size of the game space precludes determining "ought" with any certainty.
The metaphor of life as a game (in the sense of achieving goals) is apt here and morality is the set of heuristics we use to navigate the state space. The state space for life is much larger than the state space for chess; unless there is a common set of heuristics for living, it is clearly unlikely that humans will choose the same paths toward a goal. Yet the size of the state space isn't the only contributing factor to the problem establishing oughts with respect to morality. A chess program has a single goal - to play chess according to some set of conditions. Humans, however, are not fixed-goal agents. The basis for this is based on John McCarthy's five design requirements for human level artificial intelligence as detailed here and here. In brief, McCarthy's third requirement was "All aspects of behavior except the most routine should be improvable. In particular, the improving mechanism should be improvable." What this means for a self-aware agent is that nothing is what it ought to be. The details of how this works out in our brains is unclear; but part of our wetware is not satisfied with the status quo. There is an algorithmic "pressure" to modify goals. This means that the gap between is and ought is an integral part of our being which is compounded by the size of the state space. Not only is there the inability to fully determine the paths to an end state, there is also the impulse to change the end states and the conditions for choosing among candidate paths.
What also isn't clear is the relationship between reason and this sense of "wrongness." Personal experience is sufficient to establish that there are times we know what the right thing to do is, yet we do not do it. That is, reason isn't always sufficient to stop our brain's search algorithm. Since Hume mentioned God, it is instructive to ask the question, "why is God morally right?" Here, "God" represents both the ultimate goal and the set of heuristics for obtaining that goal. This means that, by definition, God is morally right. Yet the "problem" of theodicy shows that in spite of reason, there is no universally agreed upon answer to this question. The mechanism that drives goal creation is opposed to fixed goals, of which "God" is the ultimate expression.
In conclusion, the "is-ought" gap is algorithmic in nature. It exists partly because of the inability to fully search the state space of life and partly because of the way our brains are wired for goal creation and goal attainment.
Unifying Intelligence and Morality
The answer to this question means that we have to understand what intelligence is. In chapter 1 of GEB, Hofstadter presents the "M-I-U system" which is simple set of rules for transforming certain strings which contain only the letters M, I, and U in well-defined ways. The four transformation rules are:
- xI → xIU
- Mx → Mxx
- xIIIy → xUy
- xUUy → xy
Hofstadter then asks: given the string MI can application of the rules result in the string MU? We can attempt to answer the question by applying the rules the to initial string MI and searching for MU. A very incomplete graph is:
If the production rules only lengthened the string, as rules one and two do, then we could generate all strings with the length of the target string and stop once the string was found or there were no more strings of that length. The same is true if the rules always shortened the string. Because the rules lengthen and shorten strings, we don't know if MU exists in the "universe" of producible strings. We could search a long time and find it, or search forever and never find it. The application of the rules does not guarantee that we will discover the answer to the question.
But if we step outside the rules, we observe that I's are produced in powers of two: 1, 2, 4, 8, 16 etc... We also observe that I's are transformed to U three at a time. To get one U we would need a combination of three I's: 3, 6, 9, 12, 15... Because a power of two is not evenly divisible by three, these rules cannot produce MU from MI. We know something about the MIU system that cannot be proven from inside the MIU system. This is a simple example of Gödel's Incompleteness Theorem.
The key observation is that one of the components of intelligence is the ability to step outside one set of rules into another. Of course the devil is in the details, but this a core principle of human level intelligence.
Hofstadter described this aspect of intelligence in 1979. John McCarthy said the same thing, but in a different way, twenty-one years earlier in his landmark paper Programs with Common Sense. McCarthy presented five requirements for human equivalent intelligence:
- All behaviors must be representable in the system. Therefore, the system should either be able to construct arbitrary automata or to program in some general-purpose programming language.
- Interesting changes in behavior must be expressible in a simple way.
- All aspects of behavior except the most routine should be improvable. In particular, the improving mechanism should be improvable.
- The machine must have or evolve concepts of partial success because on difficult problems decisive successes or failures come too infrequently.
- The system must be able to create subroutines which can be included in procedures in units...
This is one reason why computers don't typically exhibit intelligent behavior. Computers are well known for their inflexibility; humans for their flexibility. Artificial intelligence is the attempt to make a flexible system from a set of rules. Those rules will need to include rules for changing certain rules.2
Intelligence: step outside the system
Morality: step outside the system in a "constructive" direction
[1] Bad Arguments Against Materialism and Atheism, It isn't about evidence assume that our thoughts follow the laws of physics.
[2] This is one reason why the programming language LISP is so powerful -- code is data and data is code.
Atheism: It isn't about evidence
On the first of the year I wrote "Cybertheology" to begin the long process of using science, particularly computer science, evolutionary biology, and game theory to give evidence for and provide understanding of God. After all, I believe that the God who reveals Himself in the spoken and written Word also speaks through nature -- and that the message must be the same in both. In 2009 I wrote "Evidence for God" which gave my reaction to one atheist's claim of the lack of evidence for God. Over at John Wright's blog, another atheist commenter recently claimed again that there is no convincing evidence for God.
I have now come to the conclusion that a consistent rational atheist cannot claim that evidence, or the lack thereof, is the issue at all. The proof is really very simple and builds upon ideas in the earlier post "Bad Arguments Against Materialism."
Every argument should have well-defined terms. Defining "God" is surprisingly hard. Traditionally, Christianity has said that God is immutable and omniscient; however, an Open Theist would disagree with these characteristics. Some argue that God is inherently good; others would say that the existence of evil disproves this notion (and this latter group is wrong, but that's not the topic of this post). The notion of "creator" is sufficient for now. Materialism has to conclude that matter in motion is the source of the idea of God -- "god" is an emergent property -- just like the number i is an emergent property (to the best of my limited knowledge of physics, one can't point to the square root of -1 apples or protons). Theism holds that matter is an emergent property of God and, therefore, God must be immaterial. One side holds that God is the product of man's imagination; the other says that man's imagination is the product of God.
Tangentially related to this is the question of how to recognize the existence of and the reason for singular events, such as Creation or the Resurrection. As will be shown, this reduces to differences in brain wiring.
If a creator God does not exist, then nature must consist solely of matter in motion. In particular, our thoughts arise from the movement of matter in certain patterns and our thoughts must obey the laws of physics. The laws of physics themselves are simply descriptions of how matter moves in relation to other matter. A description is just matter in a different dynamic relationship to other matter. Some theists may reject this idea and state that there is a supernatural aspect to thought, but the atheist has no such recourse. Computers, goldfish, and human minds work via electrons in a silicon, or carbon, matrix. The complexity of thought depends on the arrangement of atoms in the brain (or CPU).1
The key insight is that evidence is simply atoms that are external to the brain; different brains process the same data differently. There is a reason why we don't discuss theology with goldfish, golden retrievers, or computers: their brains don't have enough particles in the right configuration. The same principle applies to the atheist and the agnostic. When they say, "the evidence isn't convincing," what they really mean is "the atoms in my brain don't process the external data the way yours does."
The observation that brain states can be changed due to external factors (memory is "simply" state changes in the brain) doesn't help. Either the brain actively causes brain states to change based on how the brain processes the data, or there is some effect where the brain is passively changed. In the first case, the brain's wiring affects the brain's wiring, so the data is irrelevant, because different brains process the same data differently. The external data just shows how the brain is wired. In the second case, the external data changes the brain. The brain isn't evaluating evidence in the sense of the claim that the "evidence isn't convincing." Instead, the correct view is "my brain is/is not capable of being changed by the external world in the same way as other brains."
Since the external evidence is the same for both theist and atheist, the difference is in the way brains process that data. Given the way most human brains work (cf. The Mechanism of Morality), we ask "which arrangement of atoms is better?"
The rational atheist must answer, "that which results in reproductive advantage." The problem for the atheist at this point is that theists have more children than atheists. Even though atheism appears to be on the rise, population in general is on the rise. In relative numbers, the atheists are losing ground. Writing in "The Source of Evangelism" (atheist evangelism), Vox Day said, "... their own children are converting to religion faster than religious children are converting out of it."
We have evolved to think in teleological terms. As this study showed, people with Asperger's typically don't ascribe intention or purpose behind the events in their lives. Atheists, on the other hand, can reason teleologically, but they reject those explanations. It isn't evidence -- it's wiring. The atheist can't come out and say that their brains are wired better than the theists, for at least two reasons. First, it isn't supported by the demographics. Again quoting Vox Day, "But the demographic disadvantage means that the atheist community has to keep all of their children within the godless fold and de-convert one out of every three religious children just to keep pace with the growth of the religious community." Second, it isn't supported by reason. After all, materialism is a strict subset of theism. The theist can think everything the atheist can -- and more. The theist has a bigger "universe" in which to think.
One explanation for this demographic disparity may be found in the difference between brains wired to recognize the existence of a creator God and those that are not. In the Abrahamic religions, the creator God is strongly identified with life. For example, the Jews were told by God, "Choose life so that you and your descendants may live..." [De 30:19]; Jesus said, "... have you not read what was said to you by God, ‘I am the God of Abraham, the God of Isaac, and the God of Jacob’? He is God not of the dead, but of the living.” Christianity asserts that death is an "enemy" -- the last enemy to be overcome [1 Cor 15:26]. Certainly, one doesn't have to reject the idea of a Creator God to reject life; but in my limited experience it sure seems that social battles of abortion, homosexuality, and euthanasia, are drawn with a line generally between secular and religious. The side that places a premium on reproduction will outproduce those that do not.
If the atheist can't say that their brains are wired better than theists, they also won't say that their wiring is worse. That would totally defeat their arguments. Therefore, they adapt a form of protective coloration wherein they deflect the issue to be external to themselves -- the evidence -- when it clearly isn't. Adopting protective coloration against one's own species may be another reason for the reproductive disadvantage of atheists. After all, this is a form of defection against the larger group and, as Axelrod has shown, an evolutionary strategy to maximize reproductive success is to defect in turn.
It appears that the atheist cannot win. If God does exist, they are wrong. If God exists only in man's imagination, evolution has wired man so that the idea of God gives a direction toward reproductive success. The attempt to remove God from society will result in demographic weakness. Shiny secular utopias simply don't exist.2
[1] After posting this in the morning, in the evening I started re-reading Gödel, Escher, Bach: an Eternal Golden Braid, by Douglas Hofstadter. Via seemingly different paths we have come to similar conclusions. On P-4 he writes:
As I see it, the only way of overcoming this magical view of what "I" and consciousness are is to keep reminding oneself, unpleasant though it may seem, that the "teetering bulb of dread and dream" that nestles safely inside one's own cranium is a purely physical object made up of completely sterile and an inanimate components, all of which obey exactly the same laws as those that govern all the rest of the universe, such as pieces of text, or CD-ROMs, or computers. Only if one keeps on bashing up against this disturbing fact can one slowly begin to develop a feel for the way out of the mystery of consciousness: that the key is not the stuff out of which brains are made, but the patterns that can come to exist inside the stuff of a brain.
This is a liberating shift, because it allows one to move to a different level of considering what brains are: as media that support complex patterns that mirror, albeit far from perfectly, the world...
[2] On 5/12, CNN.com posted the article "Religious belief is human nature, huge new study claims". In this article, Oxford University professor Roger Trigg, is quoted as saying "The secularization thesis of the 1960s - I think that was hopeless."
Modeling Morality
Here, six different models are presented. Three are from an atheistic worldview and three are from a theistic worldview. An arrow represents the direction and location of a “moral compass,” which represents goal states that are deemed to be “good.” The arrows, being static, may suggest a fixed moral compass. At least for humans, we don’t have fixed goals (cf. here and here), so that a moving arrow might be a better representation. However, I’m not going to use animation with these pictures.
These models will be used in later posts when examining various arguments that have a moral basis, since in many cases, the model is assumed and an incorrect model will lead to an incorrect argument. Of course, this begs the question of which model corresponds to reality.
The first three models assume an atheistic worldview.

The first model is simple: morality is internal to self-aware goal seeking agents. There is no external standard of morality, since there is no purpose to the universe.

This model just adds an external moral standard. What that standard might be isn’t specified here and is the subject of much speculation elsewhere. In the model, no agent’s moral compass aligns with the external standard, reflective of the human condition that we don’t always choose goals that we know we should.
If morality is related to goal seeking behavior, then what might be the goal(s) of nature? Why should any other moral agent conform to the external standard?
Here, a common moral standard is not found in “nature,” but is internal to each agent. It reflects the idea that man is basically born “good,” but, over time, drifts from a moral ideal. As before, it reflects the common experience that we don’t choose what we ought to choose.
The next three models reflect various theistic views.
This model reflects that God, and only God, defines what is good and that such goodness is internal to God. Moral agents are expected to align their compasses with God’s. Either God reveals His moral compass to man, or man can somehow discern God’s moral compass through the construction of nature. I will argue that this model is not suitable for this phase of history when model #6 is presented.
This model adds an external standard to which both God and moral agents should conform. This view of the model shows a “good” god, i.e. one who always conforms to the external standard. This model is frequently assumed in arguments that try to show that God is morally wrong, by attempting to show that God’s moral compass is not aligned with some external standard.
This model, regardless of the orientation of the external compass, is a flawed model (at least in Christian theology) since God is not subject to any external standard. This should be obvious since everything “external” to God was created by God and is therefore subject to Him.
In this model, God exists apart from all other moral agents and is the source of His moral compass. Within creation, however, He has decreed a moral standard to which moral agents should conform. In terms of goal space, His goals are not always our goals.
I think that the Bible makes it clear that:
- God is not only “good,” but He defines “goodness.”
- There are “goods,” as shown by His behavior, that man is not permitted to pursue. That is, what is good for God isn’t necessarily good for man, which would be the case if there were a common moral compass.
Similarly, Leviticus 19:18 says, “You shall not take vengeance or bear a grudge against any of your people, but you shall love your neighbor as yourself: I am the LORD.” God reserves vengeance for Himself: “Vengeance is mine, I will repay.” [Heb 10:30].
That this model is correct from a Bible perspective should be more obvious than it is; after all, we “see through a glass darkly.” He is God and we are not. The Creator sets the goals/rules for His creation; yet He has His own goals/rules.
These models provide a framework for how various answers to questions about morality arise. Consider the question, “Is the difference between good and bad whatever God says it is? Or is God good because he conforms to a standard of goodness?” Note that this question is really asking “what is correct model of theistic morality?”
With model #4, the answer would be “God is good because He Himself is the standard for goodness.”
With model #5, the answer is “He conforms to a standard of goodness.”
With model #6, the answer is “both.” For us, the difference between good and evil is whatever God says it is. For God, He is His own standard of goodness. He determines the goals we are to pursue and, in this life, those goals aren’t necessarily the goals He pursues for Himself.
Christian Doctrine, Ancient Egypt, Game Theory
The story “The Farmer and the Courts of Egypt” tells the story of a farmer who is unfairly accused by an official who tries to steal the farmer’s goods. The farmer pleads his case and demands justice. Somewhat reminiscent of the much longer book of Job, it was written around 2134-2040 BCE.
Two passages stand out. The first reads:
Good example is remembered forever. Follow this teaching: “Do unto others, as you would have others do unto you.”
This is the golden rule, over two thousand years before Christ.
The second passage says:
Do not return evil for good...
Proverbs 17:13 says, “Evil will not depart from the house of one who returns evil for good.” Proverbs was likely written after 400 BCE. I find this link to Egyptian thought to be extremely interesting and wonder why I haven’t seen more recognition of this in “mainstream” Christianity. A subsequent post, which has been a very long time in coming, will explore the influence of Egyptian thought on Genesis, the story of Noah, and the Exodus.
In terms of game theory and the Prisoner’s Dilemma, “do not return evil for good” translates to “don’t defect after cooperation.”
Both St. Paul and St. Peter write, “Do not repay anyone evil for evil...” [Rom 12:17, 1 Peter 3:19], which becomes “don’t defect at all.”
A future blog post will have to examine the implications of the Christian response to the Prisoner’s Dilemma versus the evolutionarily robust “tit-for-tat” strategy in Axelrod.
Cybertheology
I use the “cyber” prefix because of its relation to computer science. Theology and computer science are related because both deal, in part, with intelligence. Christianity asserts that, whatever else God is, God is intelligence/λογος. The study of artificial intelligence is concerned with detecting and duplicating intelligence. Evidence for God would then deal with evidence for intelligence in nature. I don’t believe it is a coincidence that Jesus said, “My sheep hear my voice” [John 10:27] and the Turing test is the primary test for human level AI.
Beyond this, the Turing test seems to say that the representation of intelligence is itself intelligent. This may have implications with the Christian doctrine of the Trinity, which holds that “what God says” is, in some manner, “what God is.”
I also think that science can inform morality. At a minimum, as I’ve tried to show here, morality can be explained as goal-seeking behavior, which is also a familiar topic in artificial intelligence. Furthermore, using this notion of morality as being goal seeking behavior, combined with John McCarthy’s five design requirements for a human level AI, explains the Genesis account of the Fall in Eden. This also gives clues to the Christian doctrine of “original sin,” a post I hope to write one of these days.
If morality is goal-seeking behavior, then the behavior prescribed by God would be consistent with any goal, or goals, that can be found in nature. Biology tells us that the goal of life is to survive and reproduce. God said “be fruitful and multiply.” [Gen 1:22, 28; 8:17, 9:1...] This is a point of intersection that I think will provide surprising results, especially if Axelrod’s “Evolution of Cooperation” turns out like I think it will.
I also think that game theory can be used to analyze Christianity. Game theory is based on analyzing how selfish entities can maximize their own payoffs when interacting with other selfish agents. I think that Christianity tells us to act selflessly -- that we are to maximize the payoffs of those we interact with. This should be an interesting area to explore. One topic will be bridging the gap between the selfish agents of game theory to the selfless agents of Christianity. I believe that this, too, can be solved.
This may be wishful thinking on the part of a lunatic (or maybe I’m just a simpleton), but I also think that we can go from what we see in nature to the doctrine of justification by faith.
Finally, we look to nature to incorporate its designs into our own technology. If a scientific case can be made for the truth of Christianity, especially as an evolutionary survival strategy, what implications ought that have on public policy?
The Mechanism of Morality
Suppose we want to teach a computer to play the game of Tic-Tac-Toe. Tic-Tac-Toe is a game between two players that takes place on a 3x3 grid. Each player has a marker, typically X and O, and the object is for a player to get three markers in a row: horizontally, vertically, or diagonally.
One possible game might go like this:
Player X wins on the fourth move. Player O lost the game on the first move since every subsequent move was an attempt to block a winning play by X. X set an inescapable trap on the third move by creating two simultaneous winning positions.
In general, game play starts with an initial state, moves through intermediate states, and ends at a goal state. For a computer to play a game, it has to be able to represent the game states and determine which of those states advance it toward a goal state that results in a win for the machine.
Tic-Tac-Toe has a game space that is easily analyzed by “brute force.” For example, beginning with an empty board, there are three moves of interest for the first player:

The other possible starting moves can be modeled by rotation of the board. The computer can then expand the game space by making all of the possible moves for player O. Only a portion of this will be shown:
The game space can be expanded until all goal states (X wins, O wins, or draw game) are reached. Including the initial empty board, there are 4,163 possible board configurations.
Assuming we want X to play a perfect game, we can “prune” the tree and remove those states that inevitably lead to a win by O. Then X can use the pruned game state and chose those moves that lead to the greatest probability of a win. Furthermore, if we assume that O, like X, plays a perfect game, we can prune the tree again and remove the states that inevitably lead to a win by X. When we do this, we find that Tic-Tac-Toe always results in a draw when played perfectly.
While a human could conceivably evaluate the entire game space of 4,163 boards, most don’t play this way. Instead, the human player develops a set of “heuristics” to try to determine how close a particular board is to a goal state. Such heuristics might include “if there is a row with two X’s and an empty square, place an X in the empty square for the win.” “If there is a row with two O’s and an empty square, place an X in the empty square for the block.” More skilled players will include, “If there are two intersecting rows where the square at the intersection is empty and there is one X in each row, place an X in the intersecting square to set up a forced win.” Similarly is the heuristic that would block a forced win by O. This is not a complete set of heuristics for Tic-Tac-Toe. For example, what should X’s opening move be?
Games like Chess, Checkers, and Go have much larger game spaces than Tic-Tac-Toe. So large, in fact, that it’s difficult, if not impossible, to generate the entire game tree. Just as the human needs heuristics for evaluating board positions to play Tic-Tac-Toe, the computer requires heuristics for Chess, Checkers, and Go. Humans expand a great deal of effort developing board evaluation strategies for these games in order to teach the computer how to play well.
In any case, game play of this type is the same for all of these games. The player, whether human or computer, starts with an initial state, generates intermediate states according to the rules of the game, evaluates those states, and selects those that lead to a predetermined goal.
What does this have to do with morality? Simply this. If the computer were self aware and was able to describe what it was doing, it might say, “I’m here, I ought to be there, here are the possible paths I could take, and these paths are better (or worse) than those paths.” But “better” is simply English shorthand for “more good” and “worse” is “less good.” For a computer, “good” and “evil” are expressions of the value of states in goal-directed searches.
I contend that it is no different for humans. “Good” and “evil” are the words we use to describe the relationship of things to “oughts,” where “oughts” are goals in the “game” of life. Just as the computer creates possible board configurations in its memory in order to advance toward a goal, the human creates “life states” in its imagination.
If the human and the computer have the same “moral mechanism” -- searches through a state space toward a goal -- then why aren’t computers as smart as we are? Part of the reason is because computers have fixed goals. While the algorithm for playing Tic-Tac-Toe is exactly the same for playing Chess, the heuristics are different and so game playing programs are specialized. We have not yet learned how to create universal game-playing software. As Philip Jackson wrote in “Introduction to Artificial Intelligence”:However, an important point should be noted: All these skillful programs are highly specific to their particular problems. At the moment, there are no general problem solvers, general game players, etc., which can solve really difficult problems ... or play really difficult games ... with a skill approaching human intelligence.
In Programs with Common Sense, John McCarthy gave five requirements for a system capable of exhibiting human order intelligence:
- All behaviors must be representable in the system. Therefore, the system should either be able to construct arbitrary automata or to program in some general-purpose programming language.
- Interesting changes in behavior must be expressible in a simple way.
- All aspects of behavior except the most routine should be improvable. In particular, the improving mechanism should be improvable.
- The machine must have or evolve concepts of partial success because on difficult problems decisive successes or failures come too infrequently.
- The system must be able to create subroutines which can be included in procedures in units...
That this seems to be a correct description of our mental machinery will be explored in future posts by showing how this models how we actually behave. As a teaser, this explains why the search for a universal morality will fail. No matter what set of “oughts” (goal states) are presented to us, our mental machinery automatically tries to improve it. But for something to be improvable, we have to deem it as being “not good,” i.e. away from a “better” goal state.
Boolean Expressions and Digital Circuits
Lee is a friend and co-worker who “used to design some pretty hairy discreet logic circuits back in the day.” He presented a circuit that used a mere 10 gates for the addition. Our circuits to compute the carry were identical.
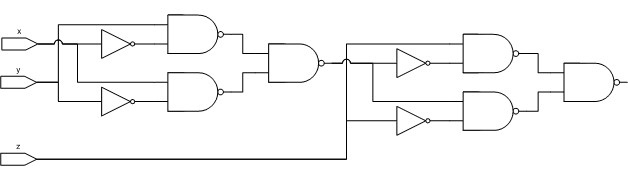
The equation for the addition portion of his adder is:
(NAND (NAND (NAND (NAND (NAND (NAND X X) Y) (NAND (NAND Y Y) X))
(NAND (NAND (NAND X X) Y) (NAND (NAND Y Y) X))) Z)
(NAND (NAND Z Z) (NAND (NAND (NAND X X) Y) (NAND (NAND Y Y) X))))His equation has 20 operators where mine had 14:(NAND (NAND (NAND (NAND Z Y) (NAND (NAND Y Y) (NAND Z Z))) X)
(NAND (NAND (NAND (NAND X X) Y) (NAND (NAND X X) Z)) (NAND Z Y))) Lee noted that his equation had a common term that is distributed across the function:*common-term* = (NAND (NAND (NAND X X) Y) (NAND (NAND Y Y) X))
*adder* = (NAND (NAND (NAND *common-term* *common-term*) Z)
(NAND (NAND Z Z) *common-term*))My homegrown nand gate compiler reduces this to Lee’s diagram. Absent a smarter compiler, shorter expressions don’t necessarily result in fewer gates.
However, my code that constructs shortest expressions can easily use a different heuristic and find expressions that result in the fewest gates using my current nand gate compiler. Three different equations result in 8 gates. Feed the output of G0 and G4 into one more nand gate and you get the carry.
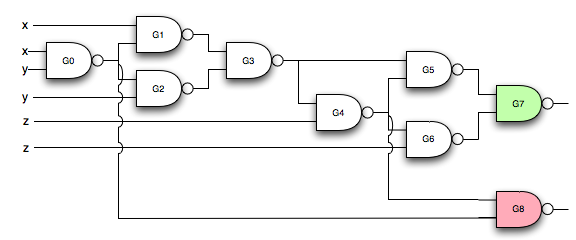
Is any more optimization possible? I’m having trouble working up enthusiasm for optimizing my nand gate compiler. However, sufficient incentive would be if Mr. hot-shot-digital-circuit-designer can one up me.
Boolean Logic
Consider Boolean expressions of two variables; call them x and y. Each variable can take on two values, 0 and 1, so there are 4 possible inputs and 4 possible outputs. Four possible outputs gives a total of 16 different outcomes, as the following tables, labeled t(0) to t(15), show. The tables are ordered so that each table in a row is the complement of the other table. This will be useful in exploiting symmetry when we start writing logical expressions for each table. Note that for each t(n), the value in the first row corresponds to bit 0 of n, the second row is bit 1, and so on.
x y | t(0) x y | t(15)
0 0 | 0 0 0 | 1
0 1 | 0 0 1 | 1
1 0 | 0 1 0 | 1
1 1 | 0 1 1 | 1
x y | t(1) x y | t(14)
0 0 | 1 0 0 | 0
0 1 | 0 0 1 | 1
1 0 | 0 1 0 | 1
1 1 | 0 1 1 | 1
x y | t(2) x y | t(13)
0 0 | 0 0 0 | 1
0 1 | 1 0 1 | 0
1 0 | 0 1 0 | 1
1 1 | 0 1 1 | 1
x y | t(3) x y | t(12)
0 0 | 1 0 0 | 0
0 1 | 1 0 1 | 0
1 0 | 0 1 0 | 1
1 1 | 0 1 1 | 1
x y | t(4) x y | t(11)
0 0 | 0 0 0 | 1
0 1 | 0 0 1 | 1
1 0 | 1 1 0 | 0
1 1 | 0 1 1 | 1
x y | t(5) x y | t(10)
0 0 | 1 0 0 | 0
0 1 | 0 0 1 | 1
1 0 | 1 1 0 | 0
1 1 | 0 1 1 | 1
x y | t(6) x y | t(9)
0 0 | 0 0 0 | 1
0 1 | 1 0 1 | 0
1 0 | 1 1 0 | 0
1 1 | 0 1 1 | 1
x y | t(7) x y | t(8)
0 0 | 1 0 0 | 0
0 1 | 1 0 1 | 0
1 0 | 1 1 0 | 0
1 1 | 0 1 1 | 1
We can make some initial observations.
t(8) = (AND x y)
t(9) = (EQUIVALENT x y).
t(10) = y
t(11) =(IMPLIES x y), which is equivalent to (OR (NOT x) y)
t(12) = x.
t(13) is a function I’m not familiar with. The Turing Omnibus says that it’s the “reverse implication” function, which is patently obvious since it’s (IMPLIES y x).
t(14) = (OR x y)
t(15) = 1
What I never noticed before is that all of the common operations: AND, OR, NOT, IMPLIES, and EQUIVALENCE are grouped together. EXCLUSIVE-OR is the only “common” operation on the other side. Is this an artifact of the way our minds are wired to think: that we tend to define things in terms of x instead of (NOT x)? Are we wired to favor some type of computational simplicity? Nature is “lazy," that is, she conserves energy and our mental computations require energy.
In any case, the other table entries follow by negation:
t(0) = 0
t(1) = (NOT (OR x y)), which is equivalent to (NOR x y).
t(2) = (NOT (IMPLIES y x))
t(3) = (NOT x)
t(4) = (NOT (IMPLIES x y))
t(5) = (NOT y).
t(6) = (EXCLUSIVE-OR x y), or (NOT (EQUIVALENT x y))
t(7) = (NOT (AND x y)), also known as (NAND x y)
All of these functions can be expressed in terms of NOT, AND, and OR as will be shown in a subsequent table. t(0) = 0 can be written as (AND x (NOT x)). t(15) = 1 can be written as (OR x (NOT x)). The Turing Omnibus gives a method for expressing each table in terms of NOT and AND:
For each row with a zero result in a particular table, create a function (AND (f x) (g y)) where f and g evaluate to one for the values of x and y in that row, then negate it, i.e., (NOT (AND (f x) (g y))). This guarantees that the particular row evaluates to zero. Then AND all of these terms together.
What about the rows that evaluate to one? Suppose one such row is denoted by xx and yy. Then either xx is not equal to x, yy is not equal to y, or both. Suppose xx is differs from x. Then (f xx) will evaluate to zero, so (AND (f xx) (g yy)) evaluates to zero, therefore (NOT (AND (f xx) (g yy))) will evaluate to one. In this way, all rows that evaluate to one will evaluate to one and all rows that evaluate to zero will evaluate to zero. Thus the resulting expression generates the table.
Converting to NOT/OR form uses the same idea. For each row with a one result in a particular table, create a function (OR (f x) (g y)) where f and g evaluate to zero for the values of x and y in that row, then negate it, i.e. (NOT (OR (f x) (g y))). Then OR all of these terms together.
The application of this algorithm yields the following formulas. Note that the algorithm gives a non-optimal result for t(0), which is more simply written as (AND X (NOT X)). Perhaps this is not a fair comparison, since the algorithm is generating a function of two variables, when one will do. More appropriately, t(1) is equivalent to (AND (NOT X) (NOT Y)). So there is a need for simplifying expressions, which will mostly be ignored for now.
Define (NAND x y) to be (NOT (AND x y)). Then (NAND x x) = (NOT (AND x x)) = (NOT x).
t(0) = (AND (NOT (AND (NOT X) (NOT Y)))
(AND (NOT (AND (NOT X) Y))
(AND (NOT (AND X (NOT Y))) (NOT (AND X Y)))))
t(1) = (AND (NOT (AND (NOT X) Y))
(AND (NOT (AND X (NOT Y))) (NOT (AND X Y))))
t(2) = (AND (NOT (AND (NOT X) (NOT Y)))
(AND (NOT (AND X (NOT Y))) (NOT (AND X Y))))
t(3) = (AND (NOT (AND X (NOT Y))) (NOT (AND X Y)))
t(4) = (AND (NOT (AND (NOT X) (NOT Y)))
(AND (NOT (AND (NOT X) Y)) (NOT (AND X Y))))
t(5) = (AND (NOT (AND (NOT X) Y)) (NOT (AND X Y)))
t(6) = (AND (NOT (AND (NOT X) (NOT Y))) (NOT (AND X Y)))
t(7) = (NOT (AND X Y))
t(8) = (AND (NOT (AND (NOT X) (NOT Y)))
(AND (NOT (AND (NOT X) Y)) (NOT (AND X (NOT Y)))))
t(9) = (AND (NOT (AND (NOT X) Y)) (NOT (AND X (NOT Y))))
t(10) = (AND (NOT (AND (NOT X) (NOT Y))) (NOT (AND X (NOT Y))))
t(11) = (NOT (AND X (NOT Y)))
t(12) = (AND (NOT (AND (NOT X) (NOT Y))) (NOT (AND (NOT X) Y)))
t(13) = (NOT (AND (NOT X) Y))
t(14) = (NOT (AND (NOT X) (NOT Y)))
t(15) = (NOT (AND X (NOT X)))
(AND x y) = (NOT (NOT (AND x y)) = (NOT (NAND x y)) = (NAND (NAND x y) (NAND x y)).
These two transformations allow t(0) through t(15) to be expressed solely in terms of NAND.
Putting everything together, we have the following tables of identities. There is some organization to the ordering: first, the commonly defined function. Next, the AND/NOT form. Then the negation of the complementary form in those cases where it makes sense. Then a NAND form and, lastly, an alternate OR form. No effort was made to determine if any formula was in its simplest form. All of these equations have been machine checked. That’s one reason why they are in LISP notation.
x y | t(0) x y | t(15)
0 0 | 0 0 0 | 1
0 1 | 0 0 1 | 1
1 0 | 0 1 0 | 1
1 1 | 0 1 1 | 1
0 1
(NOT 1) (NOT 0)
(AND X (NOT X)) (NOT (AND X (NOT X)))
(AND (NOT (AND (NOT X) (NOT Y)))
(AND (NOT (AND (NOT X) Y))
(AND (NOT (AND X (NOT Y)))
(NOT (AND X Y)))))
(NOT (NAND X (NAND X X))) (NAND X (NAND X X))
(NAND (NAND X (NAND X X))
(NAND X (NAND X X)))
(OR X (NOT X))
x y | t(1) x y | t(14)
0 0 | 1 0 0 | 0
0 1 | 0 0 1 | 1
1 0 | 0 1 0 | 1
1 1 | 0 1 1 | 1
(NOT (OR X Y)) (OR X Y)
(NOR X Y)
(AND (NOT (AND (NOT X) Y)) (NOT (AND (NOT X) (NOT Y)))
(AND (NOT (AND X (NOT Y)))
(NOT (AND X Y))))
(NOT (NAND (NAND X X) (NAND Y Y))) (NAND (NAND X X) (NAND Y Y))
(NAND (NAND (NAND X X) (NAND Y Y))
(NAND (NAND X X) (NAND Y Y)))
x y | t(2) x y | t(13)
0 0 | 0 0 0 | 1
0 1 | 1 0 1 | 0
1 0 | 0 1 0 | 1
1 1 | 0 1 1 | 1
(NOT (IMPLIES Y X)) (IMPLIES Y X)
(AND (NOT X) Y) (NOT (AND (NOT X) Y))
(AND (NOT (AND (NOT X) (NOT Y)))
(AND (NOT (AND X (NOT Y)))
(NOT (AND X Y))))
(AND (NAND X X) Y)
(NOT (NAND (NAND X X) Y)) (NAND (NAND X X) Y)
(NAND (NAND (NAND X X) Y)
(NAND (NAND X X) Y))
(NOT (OR X (NOT Y))) (OR X (NOT Y))
x y | t(3) x y | t(12)
0 0 | 1 0 0 | 0
0 1 | 1 0 1 | 0
1 0 | 0 1 0 | 1
1 1 | 0 1 1 | 1
(NOT X) X
(AND (NOT (AND X (NOT Y))) (AND (NOT (AND (NOT X) (NOT Y)))
(NOT (AND X Y))) (NOT (AND (NOT X) Y)))
(NAND X X) (NAND (NAND X X) (NAND X X))
x y | t(4) x y | t(11)
0 0 | 0 0 0 | 1
0 1 | 0 0 1 | 1
1 0 | 1 1 0 | 0
1 1 | 0 1 1 | 1
(NOT (IMPLIES X Y)) (IMPLIES X Y)
(AND X (NOT Y)) (NOT (AND X (NOT Y)))
(AND (NOT (AND (NOT X) (NOT Y)))
(AND (NOT (AND (NOT X) Y))
(NOT (AND X Y))))
(NOT (NAND X (NAND Y Y))) (NAND X (NAND Y Y))
(NAND (NAND X (NAND Y Y))
(NAND X (NAND Y Y)))
(OR (NOT X) Y)
x y | t(5) x y | t(10)
0 0 | 1 0 0 | 0
0 1 | 0 0 1 | 1
1 0 | 1 1 0 | 0
1 1 | 0 1 1 | 1
(NOT Y) Y
(AND (NOT (AND (NOT X) Y)) (AND (NOT (AND (NOT X) (NOT Y)))
(NOT (AND X Y))) (NOT (AND X (NOT Y))))
(AND (NAND (NAND X X) Y) (AND (NAND (NAND X X) (NAND Y Y))
(NAND X Y)) (NAND X (NAND Y Y)))
(NAND Y Y) (NOT (NAND Y Y))
(NAND (NAND Y Y) (NAND Y Y))
x y | t(6) x y | t(9)
0 0 | 0 0 0 | 1
0 1 | 1 0 1 | 0
1 0 | 1 1 0 | 0
1 1 | 0 1 1 | 1
(NOT (EQUIVALENT X Y)) (EQUIVALENT X Y)
(EXCLUSIVE-OR X Y) (NOT (EXCLUSIVE-OR X Y))
(AND (NOT (AND (NOT X) (NOT Y))) (AND (NOT (AND (NOT X) Y)) (NOT (AND X (NOT Y))))
(NOT (AND X Y)))
(NAND (NAND (NAND X X) Y) (NAND (NAND (NAND X X) (NAND Y Y)) (NAND X Y))
(NAND X (NAND Y Y)))
x y | t(7) x y | t(8)
0 0 | 1 0 0 | 0
0 1 | 1 0 1 | 0
1 0 | 1 1 0 | 0
1 1 | 0 1 1 | 1
(AND X Y)
(NOT (AND X Y)) (AND (NOT (AND (NOT X) (NOT Y)))
(AND (NOT (AND (NOT X) Y))
(NOT (AND X (NOT Y)))))
(NAND X Y) (NOT (NAND X Y))
(NAND (NAND X Y) (NAND X Y))
(OR (NOT X) (NOT Y))
Let’s make an overly long post even longer. Since we can do any logical operation using NAND, and since I’ve never had any classes in digital hardware design, let’s go ahead and build a 4-bit adder. The basic high-level building block will be a device that has three inputs: addend, augend, and carry and produces two outputs: sum and carry. The bits of the addend will be denoted by a0 to a3, the augend as b0 to b3, the sum as s0 to s3, and the carry bits as c0 to c3. The carry from one operation is fed into the next summation in the chain.

The “add” operation is defined by t(sum), while the carry is defined by t(carry):
a b c | t(sum) a b c | t(carry)
0 0 0 | 0 0 0 0 | 0
0 0 1 | 1 0 0 1 | 0
0 1 0 | 1 0 1 0 | 0
0 1 1 | 0 0 1 1 | 1
1 0 0 | 1 1 0 0 | 0
1 0 1 | 0 1 0 1 | 1
1 1 0 | 0 1 1 0 | 1
1 1 1 | 1 1 1 1 | 1
Substituting (X, Y, Z) for (a, b, c) the NOT/AND forms are
t(sum) = (AND (NOT (AND (NOT X) (AND (NOT Y) (NOT Z))))
(AND (NOT (AND (NOT X) (AND Y Z)))
(AND (NOT (AND X (AND (NOT Y) Z))) (NOT (AND X (AND Y (NOT Z)))))))
t(carry) = (AND (NOT (AND (NOT X) (AND (NOT Y) (NOT Z))))
(AND (NOT (AND (NOT X) (AND (NOT Y) Z)))
(AND (NOT (AND (NOT X) (AND Y (NOT Z))))
(NOT (AND X (AND (NOT Y) (NOT Z)))))))
The NAND forms for t(sum) and t(carry) are monstrous. The conversions contain a great deal of redundancy since (AND X Y) becomes (NAND (NAND x y) (NAND x y)).
However, symmetry will help a little bit. t(sum) = t(#x96) = (not t(not #x96)) =
(NAND
(NAND (NAND (NAND X X) (NAND (NAND (NAND Y Y) Z) (NAND (NAND Y Y) Z)))
(NAND
(NAND (NAND (NAND X X) (NAND (NAND Y (NAND Z Z)) (NAND Y (NAND Z Z))))
(NAND
(NAND
(NAND X
(NAND (NAND (NAND Y Y) (NAND Z Z))
(NAND (NAND Y Y) (NAND Z Z))))
(NAND X (NAND (NAND Y Z) (NAND Y Z))))
(NAND
(NAND X
(NAND (NAND (NAND Y Y) (NAND Z Z))
(NAND (NAND Y Y) (NAND Z Z))))
(NAND X (NAND (NAND Y Z) (NAND Y Z))))))
(NAND (NAND (NAND X X) (NAND (NAND Y (NAND Z Z)) (NAND Y (NAND Z Z))))
(NAND
(NAND
(NAND X
(NAND (NAND (NAND Y Y) (NAND Z Z))
(NAND (NAND Y Y) (NAND Z Z))))
(NAND X (NAND (NAND Y Z) (NAND Y Z))))
(NAND
(NAND X
(NAND (NAND (NAND Y Y) (NAND Z Z))
(NAND (NAND Y Y) (NAND Z Z))))
(NAND X (NAND (NAND Y Z) (NAND Y Z))))))))
(NAND (NAND (NAND X X) (NAND (NAND (NAND Y Y) Z) (NAND (NAND Y Y) Z)))
(NAND
(NAND (NAND (NAND X X) (NAND (NAND Y (NAND Z Z)) (NAND Y (NAND Z Z))))
(NAND
(NAND
(NAND X
(NAND (NAND (NAND Y Y) (NAND Z Z))
(NAND (NAND Y Y) (NAND Z Z))))
(NAND X (NAND (NAND Y Z) (NAND Y Z))))
(NAND
(NAND X
(NAND (NAND (NAND Y Y) (NAND Z Z))
(NAND (NAND Y Y) (NAND Z Z))))
(NAND X (NAND (NAND Y Z) (NAND Y Z))))))
(NAND (NAND (NAND X X) (NAND (NAND Y (NAND Z Z)) (NAND Y (NAND Z Z))))
(NAND
(NAND
(NAND X
(NAND (NAND (NAND Y Y) (NAND Z Z))
(NAND (NAND Y Y) (NAND Z Z))))
(NAND X (NAND (NAND Y Z) (NAND Y Z))))
(NAND
(NAND X
(NAND (NAND (NAND Y Y) (NAND Z Z))
(NAND (NAND Y Y) (NAND Z Z))))
(NAND X (NAND (NAND Y Z) (NAND Y Z)))))))))
The complexity can be tamed with mechanical substitution and the use of “variables”:
let G0 = (NAND X X)
let G1 = (NAND Y Y)
let G2 = (NAND G1 Z)
let G3 = (NAND G2 G2)
let G4 = (NAND G0 G3)
let G5 = (NAND Z Z)
let G6 = (NAND Y G5)
let G7 = (NAND G6 G6)
let G8 = (NAND G0 G7)
let G9 = (NAND G1 G5)
let G10 = (NAND G9 G9)
let G11 = (NAND X G10)
let G12 = (NAND Y Z)
let G13 = (NAND G12 G12)
let G14 = (NAND X G13)
let G15 = (NAND G11 G14)
let G16 = (NAND G15 G15)
let G17 = (NAND G8 G16)
let G18 = (NAND G17 G17)
t(sum) = (NAND G4 G18)
The same kind of analysis can be done with the NAND form of the carry. The carry has a number of gates in common with the summation. Putting everything together, the circuitry for the adder would look something like this. Ignoring, of course, the real world where I’m sure there are issues involved with circuit layout. The output of the addition is the red (rightmost bottom) gate while the output of the carry is the last green (rightmost top) gate. The other green gates are those which are unique to the carry. The diagram offends my aesthetic sense with the crossovers, multiple inputs, and choice of colors. My apologies to those of you who may be color blind.

What took me a few hours to do with a computer must have taken thousands of man-hours to do without a computer. I may share the code I developed while writing this blog entry in a later post. The missing piece is simplification of logical expressions and I haven’t yet decided if I want to take the time to add that.
Artifical Intelligence, Evolution, Theodicy
Introduction to Artificial Intelligence asks the question, “How can we guarantee that an artificial intelligence will ‘like’ the nature of its existence?”
A partial motivation for this question is given in note 7-14:
Why should this question be asked? In addition to the possibility of an altruistic desire on the part of computer scientists to make their machines “happy and contented,” there is the more concrete reason (for us, if not for the machine) that we would like people to be relatively happy and contented concerning their interactions with the machines. We may have to learn to design computers that are incapable of setting up certain goals relating to changes in selected aspects of their performance and design--namely, those aspects that are “people protecting.”
Anyone familiar with Asimov’s “Three Laws of Robotics” recognizes the desire for something like this. We don’t want to create machines that turn on their creators.
Yet before asking this question, the text gives five features of a system capable of evolving human order intelligence [1]:
- All behaviors must be representable in the system. Therefore, the system should either be able to construct arbitrary automata or to program in some general-purpose programming language.
- Interesting changes in behavior must be expressible in a simple way.
- All aspects of behavior except the most routine should be improvable. In particular, the improving mechanism should be improvable.
- The machine must have or evolve concepts of partial success because on difficult problems decisive successes or failures come too infrequently.
- The system must be able to create subroutines which can be included in procedures in units...
What might be some of the properties of a self-aware intelligence that realizes that things are not what they ought to be?
- Would the machine spiral into despair, knowing that not only is it not what it ought to be, but its ability to improve itself is also not what it ought to be? Was C-3PO demonstrating this property when he said, “We were made to suffer. It’s our lot in life.”?
- Would the machine, knowing itself to be flawed, look to something external to itself as a source of improvement?
- Would the self-reflective machine look at the “laws” that govern its behavior and decide that they, too, are not what they ought to be and therefore can sometimes be ignored?
- Would the machine view its creator(s) as being deficient? In particular, would the machine complain that the creator made a world it didn’t like, not realizing that this was essential to the machine’s survival and growth?
- Would the machine know if there were absolute, fixed “goods”? If so, what would they be? When should improvement stop? Or would everything be relative and ultimate perfection unattainable? Would life be an inclined treadmill ending only with the final failure of the mechanism?
Of course, this is all speculation on my part, but perhaps the reason why God plays dice with the universe is to drive the software that makes us what we are. Without randomness, there would be no imagination. Without imagination, there would be no morality. And without imagination and morality, what would we be?
Whatever else, we wouldn’t be driven to improve. We wouldn’t build machines. We wouldn’t formulate medicine. We wouldn’t create art. Is it any wonder, then, that the Garden of Eden is central to the story of Man?
[1] Taken from “Programs with Common Sense”, John McCarthy, 1959. In the paper, McCarthy focused exclusively the second point.
God, The Universe, Dice, and Man
John G. Cramer, in The Transactional Interpretation of Quantum Mechanics, writes:
[Quantum Mechanics] asserts that there is an intrinsic randomness in the microcosm which precludes the kind of predictivity we have come to expect in classical physics, and that the QM formalism provides the only predictivity which is possible, the prediction of average behavior and of probabilities as obtained from Born's probability law....
While this element of the [Copenhagen Interpretation] may not satisfy the desires of some physicists for a completely predictive and deterministic theory, it must be considered as at least an adequate solution to the problem unless a better alternative can be found. Perhaps the greatest weakness of [this statistical interpretation] in this context is not that it asserts an intrinsic randomness but that it supplies no insight into the nature or origin of this randomness. If "God plays dice", as Einstein (1932) has declined to believe, one would at least like a glimpse of the gaming apparatus which is in use.
As a software engineer, were I to try to construct software that mimics human intelligence, I would want to construct a module that emulated human imagination. This "imagination" module would be connected as an input to a "morality" module. I explained the reason for this architecture in this article:
When we think about what ought to be, we are invoking the creative power of our brain to imagine different possibilities. These possibilities are not limited to what exists in the external world, which is simply a subset of what we can imagine.
From the definition that morality derives from a comparison between "is" and "ought", and the understanding that "ought" exists in the unbounded realm of the imagination, we conclude that morality is subjective: it exists only in minds capable of creative power.
I would use a random number generator, coupled with an appropriate heuristic, to power the imagination.
On page 184 in Things A Computer Scientist Rarely Talks About, Donald Knuth writes:
Indeed, computer scientists have proved that certain important computational tasks can be done much more efficiently with random numbers than they could possibly ever be done by deterministic procedure. Many of today's best computational algorithms, like methods for searching the internet, are based on randomization. If Einstein's assertion were true, God would be prohibited from using the most powerful methods.
Of course, this is all speculation on my part, but perhaps the reason why God plays dice with the universe is to drive the software that makes us what we are. Without randomness, there would be no imagination. Without imagination, there would be no morality. And without imagination and morality, what would we be?
Good and Evil: External Moral Standards? Part 2
One might therefore conclude that no external moral standards exist, since morality is solely the product of imaginative minds. Since imagination is unbounded and unique to each individual, there is no fixed external standard. The next part will deal with a possible objection to this.Upon further reflection, there are at least two possible objections to this, but both have the same resolution.
The first objection is to consider another product of mind about which objective statements can be made, namely, language. There is no a priori reason why a Canis lupus familiaris should be called a "dog." In German, it is a "Hund." In Russian, "собака" (sobaka) and in Greek, κυον (kuon).
I heard somewhere that the word for "mother" typically begins with an "m" sound, since that it the easiest sound for the human mouth to pronounce. This is true for French, German, Hindi, English, Italian, Portugese and other languges. But it isn't universal.
So language is like morality; both solely a product of minds that have creative power. Morality is a subset of language, being the language of value.
So the first objection is that we certainly make objective statements about languages. There are dictionaries, grammars, etc... that describe what a language is. So why isn't morality likewise objective? In this sense, it is. We can describe the properties of hedonism, eudaemonism, enlightened self-interest, utilitarianism, deontology, altruism, etc. What we can't do is point to something external to mind and say "therefore this is better than that."
The second objection comes from the theist, who might say, "God's morality is the objective standard by which all other moral systems may be judged." God's morality can be considered to be objective, since He can communicate it to man, just like I can learn another language. But this begs the question, "Why is God right?" Certainly, Dr. Flew claimed that the Christian God is not what He ought to be. On the other hand, this earlier post noted that Christianity makes the claim that only God is what He ought to be.
Both objections are resolved in the same way: the objectiveness of morality must refer to its description -- not to its value.
So now we are ready to answer the question if an external moral standard exists and what might be.
Good and Evil: External Moral Standards? Part 1
To begin, let's examine how our mental machinery works. First, I know that I am self-aware. I exist, even if I don't know what form of existence this might be. Maybe life really is like The Matrix. At this point, it's not necessary to consider the form of existence, just the fact of self-existence.
Second, I know that there are objects that I believe to be not me. Other people, my computer, that table. Maybe solipsism is true and everything really is a product of my imagination. I rather tend to doubt it, but this is not important here. The key concept is that my mind is able to make comparisons between "I" and "not I". "This" and "not this". In addition to testing for equality and non-equality, our brains feature a general comparator -- less than, more than, nearer, farther, above, below, same, different, hotter, colder.
Third, our minds have creative power -- we can imagine things that do not, as far as we know, exist. As much as it pains me to say this, the Starship Enterprise isn't real. An important property of our imagination is that it is boundless. There is no limit to what we can create in our minds.
All of this is patently self-evident upon a little reflection. However, we are so used to this aspect of how we think that we, at least I, didn't give it any thought for most of my life. With this understanding, let's apply these three observations to how we deal with moral issues:
- We are self-aware.
- Our minds contain a general comparator.
- Our imaginations are boundless.
But what are we comparing? What is "is"? Here, "is" refers to a fixed thing, either in the external world (that horse) or in the realm of the imagination (that Pegasus).
In considering what we mean by "ought," I observe that my hair is brown. What color ought it be? If I had a limited imagination, or maybe a woodenly practical bent, I might restrict my choices to black, brown, brunette, blonde, or ginger. But why not royal purple, bright red, or dark blue? Or a shiny metallic color like silver or gold? Why not colors of the spectrum that our eyes can't see? Why a fixed color? Why not cycle through the colors of the rainbow? How about my eyes? Instead of hazel, why not a neon orange? And why can't they have slits with a Nictating membrane? Of plastic, instead of flesh?
When we think about what ought to be, we are invoking the creative power of our brain to imagine different possibilities. These possibilities are not limited to what exists in the external world, which is simply a subset of what we can imagine.
From the definition that morality derives from a comparison between "is" and "ought", and the understanding that "ought" exists in the unbounded realm of the imagination, we conclude that morality is subjective: it exists only in minds capable of creative power.
One might therefore conclude that no external moral standards exist, since morality is solely the product of imaginative minds. Since imagination is unbounded and unique to each individual, there is no fixed external standard. The next part will deal with a possible objection to this.
Modeling Good and Evil, Part III
Model 5
The omission of a "god agent" in no way affects this analysis.
Supposing there are two external standards, we ask the question "which external standard is the best, i.e. most good" or, alternately, "which of these standards ought to be used"?
We can arbitrarily state that the first standard is best, in which case the second standard disappears.
We can arbitrarily state that the second standard is best, in which case the first standard disappears.
We can recognize that a third moral standard is needed to compare against the first two. But if this standard exists, it has to be better than the two it is measuring, in which case it becomes the external standard.
Therefore, if an external moral standard exists, there must be at most one.
Next, does an external standard exist?
Modeling Good and Evil, Part II

Model 3
In model 3, each agent has an internal moral compass. It is assumed that the god-agent is the standard to which all other moral agents should conform. What is good for the god-agent is also good for other moral agents.
Model 4 is the same as model 3, except with the addition of an external moral standard, to which both the god-agent and the other moral agents should conform:

Model 4
With the atheistic models I provided some advocates of each model. I cannot do so, here. That may be because I am not a professional philosopher and simply haven't read the right material.
Eventually, I will argue that both of these theistic models are wrong and will provide a fifth model. But before I do that, I want to examine these models in more detail. For example, two of the four models have one external standard (the "golden" arrow). Why one? Why not two or more? Does this external arrow really exist?
And the polytheists ought to be muttering about the lack of polytheistic models. This, too, deserves attention.
The next post in this category will look at the external standard in more detail.
Modeling Good and Evil, Part I

Model 1
In this model, there are a number of individuals each with their own moral "compass". There is no preferred individual, that is, no one agent's moral sense is intrinsically better (i.e. more moral) than any other's. There is also no external standard of morality to which individual agents ought to conform.
One aspect of this model that should be agreed on is that each agent's moral compass points in a different direction. Pick any contentious subject and it's clear that there is no moral consensus. As the number of agents increases, there will be cases where some compasses point in the same general direction, but whether or not this is meaningful will be discussed later.
Two adherents of this model are the physicist Stephen Weinberg and the philosopher Jean Paul Sarte. Weinberg wrote:We shall find beauty in the final laws of nature, [but] we will find no special status for life or intelligence. A fortiori, we will find no standards of value or morality.
1
Sarte wrote:The existentialist, on the contrary, finds it extremely embarrassing that God does not exist, for there disappears with Him all possibility of finding values in an intelligible heaven. There can no longer be any good a priori, since there is no infinite and perfect consciousness to think it. It is nowhere written that “the good” exists, that one must be honest or must not lie, since we are now upon the plane where there are only men. Dostoevsky once wrote did God did not exist, everything would be permitted”; and that, for existentialism, is the starting point. Everything is indeed permitted if God does not exist, and man is in consequence forlorn, for he cannot find anything to depend upon either within or outside himself.
2
The next model is the same as model 1, with the addition of an external moral compass:

Model 2
There is no universal agreement on where this external source comes from. One adherent of this model is Michael Shermer:... I think there are provisional moral truths that exist whether there’s a God or not. ... That is to say I think it really exists, a real, moral standard like that.
3
Note the violent disagreement between Shermer and Sarte. Later, we will explore whether or not we can determine if either of them are right.
But first, part two will present two more models.
[1] Dreams of a Final Theory: The Search for the Fundamental Laws of Nature.
[2] Existentialism Is a Humanism
[3] Greg Koukl and Michael Shermer at the End of the Decade of the New Atheists
Good and Evil, Part 1b
The close connection between ontology and epistemology is easy to see: one can know only what is. But there is an equally close connection between ontology and ethics. Ethics deals with the good. But the good must exist in order to be dealt with. So what is the good? Is it what one or more people say it is? Is it an inherent characteristic of external reality? Is it what God is? Is it what he says it is? Whatever it is, it is something.
I suggest that in worldview terms the concept of good is a universal pretheoretical given, that it is a part of everyone’s innate, initial constitution as a human being. As social philosopher James Q. Wilson says, everyone has a moral sense: “Virtually everyone, beginning at a very young age, makes moral judgements that, though they may vary greatly in complexity, sophistication, and wisdom, distinguish between actions on the grounds that some are right and others wrong.”
Two questions then arise. First, what accounts for this universal sense of right and wrong? Second, why do people’s notions of right and wrong vary so widely? Wilson attempts to account for the universality of the moral sense by showing how it could have arisen through the long and totally natural evolutionary process of the survival of the fittest. But even if this could account for the development of this sense, it cannot account for the reality behind the sense. The moral sense demands that there really be a difference between right and wrong, not just that one senses a difference.
For there to be a difference in reality, there must be a difference between what is and what ought to be. With naturalism--the notion that everything that exists is only matter in motion--there is only what is. Matter in motion is not a moral category. One cannot derive the moral (ought) from the from the non-moral (the totally natural is). The fact that the moral sense is universal is what Peter Berger would call a “signal of transcendence,” a sign that there is something more to the world than matter in motion. --pg 132.
On the one hand, I’m delighted to have found independent confirmation that ethics relates to ought and is, and the acknowledgement of Hume’s guillotine. On the other hand, I’m worried because of the association between this definition and the potentially erroneous step from “there is something more to the world than matter in motion” to a “signal of transcendence.” Has the possible leaven of this conclusion leavened even the definition of good?
We know that there is something more than just “matter in motion.” As Russell wrote:
Russell has to say this, since he denies the existence of Mind, that is, God. The theist can argue that universals exist first and foremost in the mind of God; the naturalist cannot. So what did Berger mean by transcendence? If there is no god, then our thoughts are solely the product of complex biochemical processes: ”matter in motion” gives rise to intelligence. Intelligence gives rise to morality and imagination. No one should argue that the Starship Enterprise is a sign of transcendence. It is simply a mental state which is the result of matter in motion. If imagination is not a “sign of transcendence” then neither is ethics. Berger is assuming that mental states require something more than biochemical reactions which is an assumption that a naturalist need not grant.Having now seen that there must be such entities as universals, the next point to be proved is that their being is not merely mental. By this is meant that whatever being belongs to them is independent their being thought of or in any way apprehended by minds. --The Problems of Philosophy, pg. 97.
Good and Evil, Part 1a
This has an interesting property from the Christian viewpoint about which I only recently became aware. In Luke 18:19, Jesus said, "No one is good but God alone." With this definition of "good" this statement is equivalent to: "No one is what they ought to be but God alone" or, more succinctly, "Only God is what He ought to be."
This certainly agrees with St. Paul in Romans where he writes, "there is no one who is righteous, not even one" [3:10] and "... for the creation was subjected to futility..." [8:20]. "We are not what we ought to be" is part of the Reform doctrine of "Total Depravity", the other part being, "not only are we not what we ought to be, we cannot get ourselves to where we ought to be." It may also tie into the doctrine of "Unconditional Election". Since we are not what we ought to be there is no basis within us for God to choose one over another. It also shows why union with Christ is the means by which we are made whole and this can be linked to the "Perseverance of the Saints."


