Searle's Chinese Room Argument
[updated 9 October 2023 - Mac OS X 14 (Sonoma) no longer supports .ps files. This page now links jmc.ps to a local .pdf equivalent. Thanks ghostscript and Homebrew!].
[Work in progress... revisions to come]
Searle's "Minds, Brains, and Programs" is an attempt to show that computers cannot think the way humans do and so any effort to create human-level artificial intelligence is doomed to failure. Searle's argument is clearly wrong. What I found most interesting in reading his paper is that Searle's understanding of computers and programs can be shown to be wrong without considering the main part of the argument at all! Of course, it's possible that his main argument is right but that his subsequent commentary is in error but the main mistakes in both will be demonstrated. Then several basic, but dangerous, ideas in his paper will be exposed.
On page 11, Searle presents a dialog where he answers the following five questions (numbers added for convenience for later reference):
With 1), by saying that we are thinking machines, we introduce the "Church-Turing thesis" which states that if a calculation can be done using pencil and paper by a human, that it can also be done by a Turing machine. If Searle concludes that humans can do something that computers cannot, in theory, do, then he will have deny the C-T thesis and show that what brains do is fundamentally different from what machines do. That brains are different in kind and not in degree.
With 2), Searle runs afoul of computability theory, as brilliantly expressed by Fenynman (Simulating Physics with Computers):
So 2) doesn't help his argument and, by extension, nor does 3). It doesn't matter if the computer is digital or not (but, see here).
4) is based on a misunderstanding between "computer" and "program". We are so used to creating and running different programs on one piece of hardware that we think that there is some kind of difference between the two. But it's all hardware. Instead of the link to an article I wrote, let me demonstrate this. One of the fundamental aspects of computing is combination and selection. Binary logic is the mechanical selection of one object from two inputs. Consider this way, out of sixteen possible ways, to select one item. Note that it doesn't matter what the objects being selected are. Here we use "x" and "o", but the objects could be bears and bumblebees, or high and low pressure streams of electrons or water.
Clearly, you can't get something from nothing, so the two cases where an object is given as a result when it isn't part of the input requires a bit of engineering. Nevertheless, these devices can be built.
Along with combination and selection another aspect of computation is composition. Let's convert the above table to a device that implements the selection given two inputs in a form that can be composed again and again.

We can arrange these devices so that, regardless of which of the two inputs are given (represented by "✽"), the output is always "x":
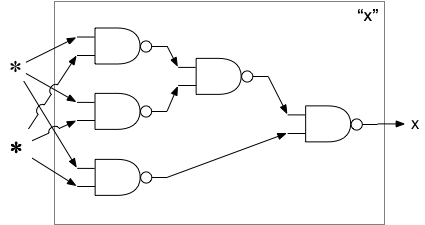
We can also make an arrangement so that the output is always "o", regardless of which inputs are used:

We now have all of the "important"1 aspects of a computer. If we replace "x" with 1 and "o" with 0 then we have all of the computational aspects of a binary computer. Every program is an arrangement of combination and selection operations. If it were economically feasible, we could build a unique network for every program. But the complexity would be overwhelming. One complicating factor is that the above does not support writeable memory. To go from a 0 to a 1 requires another node in the network, plus all of the machine states that can get to that node. For the fun of it, we show how the same logic device that combines two objects according to Table 1 can be wired together to provide memory:
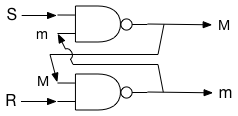
By design, S and R are initially "x", which means M and m are undefined. A continuous stream of "x" is fed into S and R.
Suppose S is set to "o" before resuming the stream of "x". Then:
S = o, M = x, R = x, m = o, S = x, M = x. This shows that when S is set to "o", M becomes "x" and stays "x".
Suppose R is set to "o" before resuming the stream of "x". Then:
R = o, m = x, S = x, M = o, R = x, m = x. This shows that when R is set to "x", M becomes "o" and stays "o", until S is reset to "o".
This shows that every program is a specification of the composition of combination and selection elements. The difference between a "computer" and a "program" is that programs are static forms of the computer: the arrangement of the elements are specified, but the symbols aren't flowing through the network.2 This means that if 1) and 2) are true, then the wiring of the brain is a program, just like each program is a logic network.
Finally, we deal with objection 5). Searle is wrong that there is no "intentionality" in the system. The "intentionality" is the way the symbols flow through the network and how they eventually interact with the external environment. Searle is right that the symbols are meaningless. So how do we get meaning from meaningless? For this, we turn to the Lambda Calculus (also here, and here: part 1, part 2). Meaning is simply a "this is that" relation. The Lambda Calculus shows how data can be associated with symbols. Our brains take in data from our eyes and associate it with a symbol. Our brains take in data from our ears and associate it with another symbol. If what we see is coincident with what we hear, we can add a further association between the "sight" symbol and the "hearing" symbol.3
The problem, then, is not with meaning, but with the ability to distinguish between symbols. The Lambda Calculus assumes this ability. We get meaning out of meaningless symbols because we can distinguish between symbols. Being able to distinguish between things is built into Nature: positive and negative charge is one example.
So Searle's dialog fails, unless you deny the first point and hold that we are not thinking machines. That is, we are something else that thinks. But this denies what we know about brain physiology.
But suppose that Searle disavows his dialog and asks that his thesis be judged solely on his main argument.
[1] This is not meant to make light of all of the remaining hard parts of building a computer. But those details are to support the process of computation: combination, selection, and composition.
[2] One could argue that the steps for evaluating Lambda expressions (substitution, alpha reduction, beta reduction) are the "computer" and that the expressions to be evaluated are the "program". But the steps for evaluating Lambda expressions can be expressed as Lambda expressions. John McCarthy essentially did this with the development of the LISP programming language (here particularly section 4, also here). Given the equivalence of the Lambda Calculus, Turing machines, and implementations of Turing machines using binary logic, the main point stands.
[3] This is why there is no problem with "qualia".
[Work in progress... revisions to come]
Searle's "Minds, Brains, and Programs" is an attempt to show that computers cannot think the way humans do and so any effort to create human-level artificial intelligence is doomed to failure. Searle's argument is clearly wrong. What I found most interesting in reading his paper is that Searle's understanding of computers and programs can be shown to be wrong without considering the main part of the argument at all! Of course, it's possible that his main argument is right but that his subsequent commentary is in error but the main mistakes in both will be demonstrated. Then several basic, but dangerous, ideas in his paper will be exposed.
On page 11, Searle presents a dialog where he answers the following five questions (numbers added for convenience for later reference):
1) "Could a machine think?"
The answer is, obviously, yes. We are precisely such machines.
2) "Yes, but could an artifact, a man-made machine think?"
Assuming it is possible to produce artificially a machine with a nervous system, neurons with axons and dendrites, and all the rest of it, sufficiently like ours, again the answer to the question seems to be obviously, yes. If you can exactly duplicate the causes, you could duplicate the effects. And indeed it might be possible to produce consciousness, intentionality, and all the rest of it using some other sorts of chemical principles than those that human beings use. It is, as I said, an empirical question.
3) "OK, but could a digital computer think?"
If by "digital computer" we mean anything at all that has a level of description where it can correctly be described as the instantiation of a computer program, then again the answer is, of course, yes, since we are the instantiations of any number of computer programs, and we can think.
4) "But could something think, understand, and so on solely in virtue of being a computer with the right sort of program? Could instantiating a program, the right program of course, by itself be a sufficient condition of understanding?"
This I think is the right question to ask, though it is usually confused with one or more of the earlier questions, and the answer to it is no.
5) "Why not?"
Because the formal symbol manipulations by themselves don't have any intentionality; they are quite meaningless; they aren't even symbol manipulations, since the symbols don't symbolize anything. In the linguistic jargon, they have only a syntax but no semantics. Such intentionality as computers appear to have is solely in the minds of those who program them and those who use them, those who send in the input and those who interpret the output.
With 1), by saying that we are thinking machines, we introduce the "Church-Turing thesis" which states that if a calculation can be done using pencil and paper by a human, that it can also be done by a Turing machine. If Searle concludes that humans can do something that computers cannot, in theory, do, then he will have deny the C-T thesis and show that what brains do is fundamentally different from what machines do. That brains are different in kind and not in degree.
With 2), Searle runs afoul of computability theory, as brilliantly expressed by Fenynman (Simulating Physics with Computers):
Computer theory has been developed to a point where it realizes that it doesn't make any difference; when you get to a universal computer, it doesn't matter how it's manufactured, how it's actually made.
So 2) doesn't help his argument and, by extension, nor does 3). It doesn't matter if the computer is digital or not (but, see here).
4) is based on a misunderstanding between "computer" and "program". We are so used to creating and running different programs on one piece of hardware that we think that there is some kind of difference between the two. But it's all hardware. Instead of the link to an article I wrote, let me demonstrate this. One of the fundamental aspects of computing is combination and selection. Binary logic is the mechanical selection of one object from two inputs. Consider this way, out of sixteen possible ways, to select one item. Note that it doesn't matter what the objects being selected are. Here we use "x" and "o", but the objects could be bears and bumblebees, or high and low pressure streams of electrons or water.
Table 1 object 1 object 2 result x x o x o x o x x o o x
Clearly, you can't get something from nothing, so the two cases where an object is given as a result when it isn't part of the input requires a bit of engineering. Nevertheless, these devices can be built.
Along with combination and selection another aspect of computation is composition. Let's convert the above table to a device that implements the selection given two inputs in a form that can be composed again and again.
We can arrange these devices so that, regardless of which of the two inputs are given (represented by "✽"), the output is always "x":

We can also make an arrangement so that the output is always "o", regardless of which inputs are used:

We now have all of the "important"1 aspects of a computer. If we replace "x" with 1 and "o" with 0 then we have all of the computational aspects of a binary computer. Every program is an arrangement of combination and selection operations. If it were economically feasible, we could build a unique network for every program. But the complexity would be overwhelming. One complicating factor is that the above does not support writeable memory. To go from a 0 to a 1 requires another node in the network, plus all of the machine states that can get to that node. For the fun of it, we show how the same logic device that combines two objects according to Table 1 can be wired together to provide memory:

By design, S and R are initially "x", which means M and m are undefined. A continuous stream of "x" is fed into S and R.
Suppose S is set to "o" before resuming the stream of "x". Then:
S = o, M = x, R = x, m = o, S = x, M = x. This shows that when S is set to "o", M becomes "x" and stays "x".
Suppose R is set to "o" before resuming the stream of "x". Then:
R = o, m = x, S = x, M = o, R = x, m = x. This shows that when R is set to "x", M becomes "o" and stays "o", until S is reset to "o".
This shows that every program is a specification of the composition of combination and selection elements. The difference between a "computer" and a "program" is that programs are static forms of the computer: the arrangement of the elements are specified, but the symbols aren't flowing through the network.2 This means that if 1) and 2) are true, then the wiring of the brain is a program, just like each program is a logic network.
Finally, we deal with objection 5). Searle is wrong that there is no "intentionality" in the system. The "intentionality" is the way the symbols flow through the network and how they eventually interact with the external environment. Searle is right that the symbols are meaningless. So how do we get meaning from meaningless? For this, we turn to the Lambda Calculus (also here, and here: part 1, part 2). Meaning is simply a "this is that" relation. The Lambda Calculus shows how data can be associated with symbols. Our brains take in data from our eyes and associate it with a symbol. Our brains take in data from our ears and associate it with another symbol. If what we see is coincident with what we hear, we can add a further association between the "sight" symbol and the "hearing" symbol.3
The problem, then, is not with meaning, but with the ability to distinguish between symbols. The Lambda Calculus assumes this ability. We get meaning out of meaningless symbols because we can distinguish between symbols. Being able to distinguish between things is built into Nature: positive and negative charge is one example.
So Searle's dialog fails, unless you deny the first point and hold that we are not thinking machines. That is, we are something else that thinks. But this denies what we know about brain physiology.
But suppose that Searle disavows his dialog and asks that his thesis be judged solely on his main argument.
Addendum - 01/24/2025
The next update didn't occur until 05/04/20, which is less of an analysis of Searle's paper, but on what another philosopher wrote about Searle's paper. Here, I claimed that meaning is a this is that relation. In my latest take on Searle, a philosopher on X (nee Twitter) took issue with that. The objections that philosophers come up with are bizarre, to say the least. They can go to great lengths to hide that what they are really claiming, namely, that the brain is not Turing compatible. The problem with this is that it is a statement which can neither be proved - nor disproved - by thinking about it. It can only be asserted.[1] This is not meant to make light of all of the remaining hard parts of building a computer. But those details are to support the process of computation: combination, selection, and composition.
[2] One could argue that the steps for evaluating Lambda expressions (substitution, alpha reduction, beta reduction) are the "computer" and that the expressions to be evaluated are the "program". But the steps for evaluating Lambda expressions can be expressed as Lambda expressions. John McCarthy essentially did this with the development of the LISP programming language (here particularly section 4, also here). Given the equivalence of the Lambda Calculus, Turing machines, and implementations of Turing machines using binary logic, the main point stands.
[3] This is why there is no problem with "qualia".

