Goto considered harmful
(defun read-input (&optional (result nil))
(let ((value (read)))
(if (equalp value 99999)
(reverse result)
(read-input (cons value result)))))
(defun average (numbers)
(let ((n (length numbers)))
(if (zerop n)
nil
(/ (reduce #'+ numbers) n))))
(defun main ()
(let ((avg (average (read-input))))
(if avg
(format t "~f~%" (float avg))
(format t "no numbers input. average undefined.~%"))))
Round to Nearest
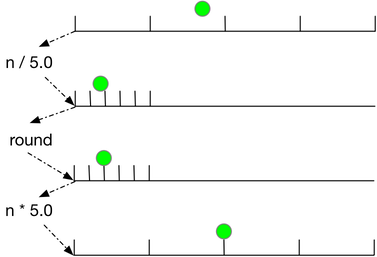
Scale the number line from 0, 5, 10, ... to 0, 1, 2, ...
Round.
Then scale from 0, 1, 2... back to 0, 5, 10...
Extension to values other than 5 is straightforward.
The Lisp code:
(defun round-to (n m)
(if (or (null m) (zerop m))
n
(* (round (/ n (float m))) (float m))))
Behold, The Power of Lisp
I was inordinately pleased with the result and have placed an order with CafePress for a coffee mug with this "Atomic Lisp" logo.

Below the fold is another take on the logo. Read More...
Static Code Analysis
This post will tie together problem representation, the power of Lisp, and the fortuitous application of the solution of an AI exercise to a real world problem in software engineering.
Problem 3-4b in Introduction to Artificial Intelligence is to find a path from Start to Finish that goes though each node only once. The graph was reproduced using OmniGraffle. Node t was renamed to node v for a reason which will be explained later.
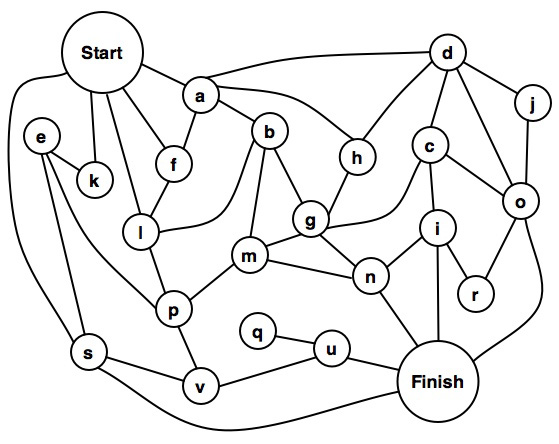
The immediate inclination might be to throw some code at the problem. How should the graph be represented? Thinking in one programming language might lead to creating a node structure that contained links to other nodes. A first cut in C might look something like this:
#define MAX_CONNECTIONS 6
typedef struct node
{
char *name;
struct node *next[MAX_CONNECTIONS];
} NODE;
extern NODE start, a, b, c, d, e, f, g, h, i, j, k;
extern NODE l, m, n, o, p, q, r, s, u, v, finish;
NODE start = {"start", {&a, &f, &l, &k, &s, NULL}};
NODE a = {"a", {&d, &h, &b, &f, NULL, NULL}};
NODE b = {"b", {&g, &m, &l, &a, NULL,NULL}};
...
Then we'd have to consider how to construct the path and whether path-walk information should be kept in a node or external to it.
If we're lucky, before we get too far into writing the code, we'll notice that there is only one way into q. Since there's only one way in, visiting q means that u will be visited twice. So the problem has no solution. It's likely the intent of the problem was to stimulate thinking about problem description, problem representation, methods for mapping the "human" view of the problem into a representation suitable for a machine, and strategies for finding relationships between objects and reasoning about them.
On the other hand, maybe the graph is in error. After all, the very first paragraph of my college calculus textbook displayed a number line where 1.6 lay between 0 and 1. Suppose that q is also connected to v, p, m, and n. Is there a solution?
Using C for this is just too painful. I want to get an answer without having to first erect scaffolding. Lisp is a much better choice. The nodes can be represented directly:
(defparameter start '(a f l k s))
(defparameter a '(f b h d))
(defparameter b '(a l m g))
(defparameter c '(d o i g))
...
The code maps directly to the problem. Minor liberties were taken. Nodes, such as a, don't point back to start since the solution never visits the same node twice. Node t was renamed v, since t is a reserved symbol. The code is then trivial to write. It isn't meant to be pretty (the search termination test is particularly egregious), particularly efficient, or a general breadth-first search function with all the proper abstractions. Twenty-three lines of code to represent the problem and twelve lines to solve it.
One solution is (START K E S V U Q P M B L F A H G C D J O R I N FINISH).

The complete set of solutions for the revised problem is:
(START K E S V U Q P M B L F A H G C D J O R I N FINISH)
(START K E S V U Q P M B L F A H D J O R I C G N FINISH)
(START K E S V U Q P L F A H D J O R I C G B M N FINISH)
(START K E P M B L F A H G C D J O R I N U Q V S FINISH)
(START K E P M B L F A H D J O R I C G N U Q V S FINISH)
(START K E P L F A H D J O R I C G B M N U Q V S FINISH)
This exercise turned out to have direct application to a real world problem. Suppose threaded systems S1 and S2 have module M that uses non-nesting binary semaphores to protect accesses to shared resources. Furthermore, these semaphores have the characteristic that they can time out if the semaphore isn't acquired after a specified period. Eventually, changes to S1 lead to changing the semaphores in M to include nesting. So there were two systems, S1 with Mn and S2 with M. Later, both systems started exhibiting sluggishness in servicing requests. One rare clue to the problem was that semaphores in Mn were timing out. No such clue was available for M because M did not provide that particular bit of diagnostic information. On the other hand, the problem seemed to exhibit itself more frequently with M than Mn. One problem? Two? More?
Semaphores in M and Mn could be timing out because of priority inversion. Or maybe there was a rare code path in M where a thread tried to acquire a semaphore more than once. That would explain the prevalence of the problem in S2 but would not explain the problem in S1.
This leads to at least two questions:
- What change in S1 necessitated adding support for nesting to the semaphores in Mn?
- Is there a code path in M where a semaphore tries to nest?
(defparameter func_1 '(func_2 acquire sem_1 acquire sem_2
func_10 func_4 release sem_2 release sem_1))
A function that requires a semaphore be held could be described by:
(defparameter func_4 '(demand sem_2))
The description of a benign function:
(defparameter func_7 '())
It's then easy to write code which walks these descriptions looking for pathological conditions. Absent a C/C++ to Lisp translator, the tedious part is creating the descriptions. But this is at least aided by the pathwalker complaining if a function definition isn't found and is far less error prone than manual examination of the code paths. Would I have used this method to analyze the code if I hadn't just done the AI problem? I hope so, but sometimes the obvious isn't.
After completing the descriptions for S1, the addition of one function call to an existing function in M was the basis for changing the semaphores so that they nested. The descriptions for S2 are not yet complete.
Super Programming Langauge, Addendum
In Introduction To Artificial Intelligence, Philip Jackson wrote:
One of the things I never liked about Pascal was that the writeln function couldn't be written in Pascal. C is deficient in that, unlike Pascal, functions cannot be nested. And so it goes.One final thing to note on the subject of reasoning programs is that the language used by an RP will typically be changed with time by the RP. We should expect in general that a reasoning program will find it necessary to define new words or to accept definitions of new words; some of these words will denote new situations, actions, phenomena, or relations--the RP may have to infer the language it uses for solving a problem. Our most important requirement for the initial language is that any necessary extensions to it be capable of being easily added to it.
The Myth of the Super Programming Language?
Jonathan Edwards, in his post The Myth of the Super Programming Language, argues that programmer productivity is due to the ability of the programmer and not the capabilities of the language. Edwards states, "It doesn’t matter what language a great programmer uses – they will still be an order of magnitude more productive than an average programmer, also regardless of what that programmer uses."
We have known for many years that some programmers are far more productive than others. In chapter three of The Mythical Man Month, Fred Brooks wrote:
So I take no exception to the statement that some programmers are more productive than others due simply to native ability, regardless of language choice. And in some circumstances, I don't disagree with Edward's statement that "it doesn't matter what language a great programmer uses". All things being equal, the great programmer will outperform the mediocre or poor programmer.Programming managers have long recognized wide productivity variations between good programmers and poor ones. But the actual measured magnitudes have astounded all of us. In one of their studies, Sackman, Erikson, and Grant were measuring performances of a group of experienced programmers. Within just this group the ratios between best and worst performances averaged about 10:1 on productivity measurements and an amazing 5:1 on program speed and space measurements!
But language does matter. For most of us, language constrains how we think. George Orwell, in 1984, described the development of the language "Newspeak." The purpose of the development of this language was to restrict the range of thought by restricting vocabularly so that the very idea of revolution against the totalitarian regime was literally unthinkable. If language can restrict thought, language can enable thought. The genius may transcend the restrictions of language and invent new ways to express what had not been expressed before. The bright may learn how to think in new ways when given a language with new idioms. The mediocre will likely think the same way, regardless of the language. Certainly, many of are are familiar with the phrase "FORTRAN with semicolons".
I am a native speaker of English. Learning German didn't prove too difficult; the languages are similar enough that, at least for me, there isn't a big switch in the way I think in either language. Perhaps this is an artifact of my not knowing German as well as I should. On the other hand, I do have to change my mindset when dealing with the language of the New Testament, Koine Greek. I can think things in Koine Greek which are not easy to translate into English.
What is true of natural languages is true of programming languages.
In his bio, Edwards says that he has been programming since 1969. He has me by two or three years; I taught myself BASIC in '71 or '72, followed by FORTRAN. In college I learned Pascal, Algol, COBOL, SNOBOL, and Control Data and H-P assembly languages. I tried to teach myself Lisp from Weisman's Lisp 1.5 Primer, but I gave up. I could blame it on not having a Lisp environment, but the truth is that it just didn't "click." After college, more languages followed, such as C, C++, Java, and etc...
Five years ago, I decided to give Lisp another try. I bought Seibel's Practical Common Lisp. I put Steel Bank Common Lisp and LispWorks Personal Edition on my MacBook Pro. I took both of them to Myrtle Beach on family vacation and started to learn the language in earnest. It wasn't easy. But I fell in love. As a language, Lisp enables me to think thoughts I wouldn't normally think in the other languages I know. And that's the key. Can I do anything in C that I can do in Lisp? Probably. After all, Greenspun's Tenth Rule is "Any sufficiently complicated C or Fortran program contains an ad hoc, informally-specified, bug-ridden, slow implementation of half of Common Lisp." But the pain involved in using Lisp idioms in C usually means that I use the C idiom, instead. This is one reason why I don't like using C much, anymore, even though it's used a great deal where I work. It's just too painful. It's why C programmers use C, when assembly language is equally powerful.
Edwards wrote, "The anecdotal benefits of esoteric languages are a selection effect", (emphasis his) where the selection is for programmer ability and not language capability. But if this is so, then I would expect to see comparisons of programmer productivity when the same individuals use different languages to implement the same tasks. Not long after I felt somewhat confident with Lisp (I still don't consider myself to have mastered the language), the company I work for dabbled with instituting PSP (Personal Software Process). A 3 day overview was offered for managers while a 2 week course was given to engineers. The two week course provided two large notebooks of course material which included programming exercises to be done in order to teach the methodology. I wasn't able to take the extended course, so I borrowed the materials from one of my co-workers. I didn't do much with the methodology, but I did do the programming exercises in C. Then I did them in Lisp. I found a 7-10x improvement in my performance, namely, time to implement the problem. One reason was that the Lisp code almost always required many fewer lines of code. I suspect another reason is that my mind switched from "C" to "Lisp" mode. Different idioms require different ways of thinking. For example, one of the advantages of Lisp is that I can write code that writes my code for me. That's a huge win over C, but it requires an unfamiliar way of looking at problems. I grant that this is anecdotal evidence. But it is consistent with what is known about natural languages. A master craftsman can craft using mediocre tools; but a master craftsman can do more faster with master tools.
Edwards said, "These kinds of claims are just thinly veiled bragging about how smart Lisp/Haskell programmers are. I actually agree that they are smarter. But ascribing it to the language is a form of tribalism: our language (country/race/sports team) is better than yours, so we are better than you." Granted, the exceptionally talented can lack humility. But human nature being what it is, if the gifted revel in their gifts, the mediocre can be oblivious to their mediocrity. "It can't be the language that makes you better" is a rejection of new ways of thinking, of expanding mental horizons, and a loss of potential increase in productivity. It is because they can't, or won't, embrace these new ways of thinking that they remain mired in mediocrity.
I have argued that language choice can make a big difference for the individual master craftsman. But Edwards notes when the "really smart programmers" complete an application using their "esoteric language" and move on to other things, that when the "professional programmers" come in to maintain the system, it "gets thrown out and rewritten in a normal programming language using normal techniques that normal people understand." This certainly happened with the software Graham developed. But the question of "what language is best for a team which follows the bell curve of ability" and "what language is best for master craftsmen" are two different questions. You cannot conclude that language choice has no effect of productivity by comparing these two unlike groups.
You don't give power tools to infants. But you can't say that the only difference between a handsaw and a power saw is solely due to the ability of the wielder.

