Boolean Expressions and Digital Circuits
08/20/10 07:24 PM Filed in: Computing | Natural Theology
This is a continuation of the post Simplifying Boolean Expressions. I started this whole exercise after reading the chapter “Systems of Logic” in “The Turing Omnibus” and deciding to fill some gaps in my education. In particular, as a software engineer, I had never designed a digital circuit. I threw together some LISP code and used it to help me design an adder using 27 nand gates for the portion that computes a sum from three inputs. After simplifying the equations I reduced it to 12 gates.
Lee is a friend and co-worker who “used to design some pretty hairy discreet logic circuits back in the day.” He presented a circuit that used a mere 10 gates for the addition. Our circuits to compute the carry were identical.
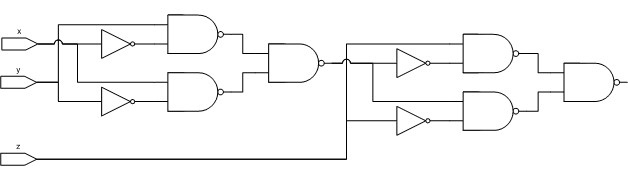
The equation for the addition portion of his adder is:
(NAND (NAND (NAND X X) Y) (NAND (NAND Y Y) X))) Z)
(NAND (NAND Z Z) (NAND (NAND (NAND X X) Y) (NAND (NAND Y Y) X))))His equation has 20 operators where mine had 14:(NAND (NAND (NAND (NAND Z Y) (NAND (NAND Y Y) (NAND Z Z))) X)
(NAND (NAND (NAND (NAND X X) Y) (NAND (NAND X X) Z)) (NAND Z Y))) Lee noted that his equation had a common term that is distributed across the function:*common-term* = (NAND (NAND (NAND X X) Y) (NAND (NAND Y Y) X))
*adder* = (NAND (NAND (NAND *common-term* *common-term*) Z)
(NAND (NAND Z Z) *common-term*))My homegrown nand gate compiler reduces this to Lee’s diagram. Absent a smarter compiler, shorter expressions don’t necessarily result in fewer gates.
However, my code that constructs shortest expressions can easily use a different heuristic and find expressions that result in the fewest gates using my current nand gate compiler. Three different equations result in 8 gates. Feed the output of G0 and G4 into one more nand gate and you get the carry.
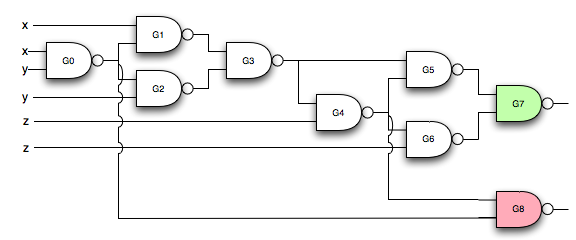
Is any more optimization possible? I’m having trouble working up enthusiasm for optimizing my nand gate compiler. However, sufficient incentive would be if Mr. hot-shot-digital-circuit-designer can one up me.
Lee is a friend and co-worker who “used to design some pretty hairy discreet logic circuits back in the day.” He presented a circuit that used a mere 10 gates for the addition. Our circuits to compute the carry were identical.

The equation for the addition portion of his adder is:
(NAND (NAND (NAND (NAND (NAND (NAND X X) Y) (NAND (NAND Y Y) X))
(NAND (NAND (NAND X X) Y) (NAND (NAND Y Y) X))) Z)
(NAND (NAND Z Z) (NAND (NAND (NAND X X) Y) (NAND (NAND Y Y) X))))His equation has 20 operators where mine had 14:(NAND (NAND (NAND (NAND Z Y) (NAND (NAND Y Y) (NAND Z Z))) X)
(NAND (NAND (NAND (NAND X X) Y) (NAND (NAND X X) Z)) (NAND Z Y))) Lee noted that his equation had a common term that is distributed across the function:*common-term* = (NAND (NAND (NAND X X) Y) (NAND (NAND Y Y) X))
*adder* = (NAND (NAND (NAND *common-term* *common-term*) Z)
(NAND (NAND Z Z) *common-term*))My homegrown nand gate compiler reduces this to Lee’s diagram. Absent a smarter compiler, shorter expressions don’t necessarily result in fewer gates.
However, my code that constructs shortest expressions can easily use a different heuristic and find expressions that result in the fewest gates using my current nand gate compiler. Three different equations result in 8 gates. Feed the output of G0 and G4 into one more nand gate and you get the carry.

Is any more optimization possible? I’m having trouble working up enthusiasm for optimizing my nand gate compiler. However, sufficient incentive would be if Mr. hot-shot-digital-circuit-designer can one up me.
blog comments powered by Disqus

