My Contribution to the Mathematical Arts
Many, many years ago, sometime in high school, I learned that the formula for computing
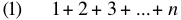
is

I'm pretty sure we were shown the geometrical derivation of this formula. In college, in late 1975 or early '76, in a Math Lab one problem asked to guess the formula for

In my handwritten lab notebook I used induction to show that the solution to (3) is:
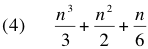
Having solved this specific case, I wanted to see if there was a general solution for any positive integer n and any positive integer exponent. Based on equations (2) and (4), I conjectured that the general solution would be a polynomial of this form:
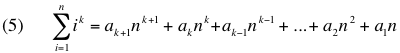
The derivation used induction on the general formula and found that the coefficients to the solution are:
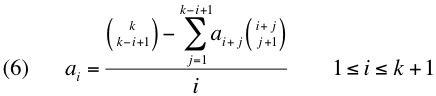
Computed coefficients for 0 <= k <= 10 are here.
Perhaps of interest are these properties of the coefficients:

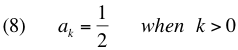

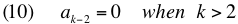
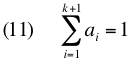
is

I'm pretty sure we were shown the geometrical derivation of this formula. In college, in late 1975 or early '76, in a Math Lab one problem asked to guess the formula for
In my handwritten lab notebook I used induction to show that the solution to (3) is:
Having solved this specific case, I wanted to see if there was a general solution for any positive integer n and any positive integer exponent. Based on equations (2) and (4), I conjectured that the general solution would be a polynomial of this form:
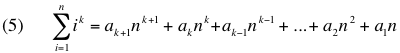
The derivation used induction on the general formula and found that the coefficients to the solution are:
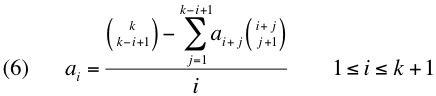
Computed coefficients for 0 <= k <= 10 are here.
Perhaps of interest are these properties of the coefficients:
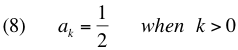

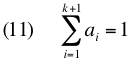
blog comments powered by Disqus

