This is a continuation of this entry which derives the general solution for the coefficients of:

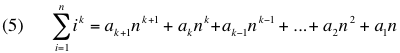
Computed coefficients for 0 <= k <= 10 were provided here.

It was noted that:

These values were determined by hand. However, it’s easy for LISP code to create the symbolic expression for each coefficient. The prefix expressions used by LISP (e.g. “(+ 3 (* 4 5) 6)” ) were converted to infix form (e.g. “(3 + (4 * 5) + 6)” ) and given to Maxima for simplification. The results are here.

What’s interesting is that the coefficients:

are all zero.

Now I have to figure out why...