Publix & Expired Products
05/28/24 11:23 AM Filed in: Life
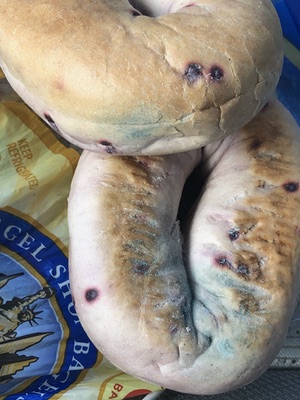


Comments
Elephant's Breath
I read this passage in Viv Albertine's "Clothes3. Music3. Boys3":
I had never heard of "elephant's breath" before. It's a paint color from the British manufacturer Farrow and Ball. This site says that the RGB values for Elephant's Breath are 204, 191, 179. ChatGPT says that the RGB values are 187, 173, 160.
Each morning I start again with the questions, easy stuff, like colour – I’ve always been drawn to colour. Mum made colour interesting for me, when I was little; she would say, ‘See the colour of that woman’s skirt? That’s called elephant’s breath.’ Or, ‘See that ribbon? It’s mint green...
I had never heard of "elephant's breath" before. It's a paint color from the British manufacturer Farrow and Ball. This site says that the RGB values for Elephant's Breath are 204, 191, 179. ChatGPT says that the RGB values are 187, 173, 160.
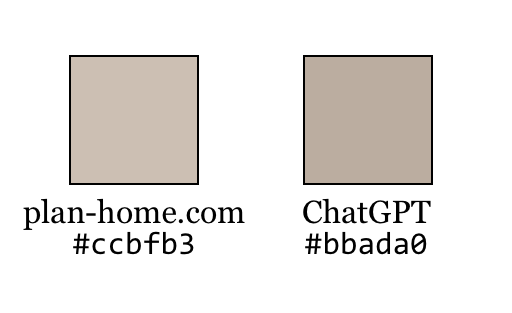
ChatGPT draws it as:
Early Family Photos
04/17/24 08:09 PM Filed in: Family
I posted a picture of my wife and I when we were married here. She just came across these old pictures (click for bigger):
circa 1989
1991
1993
Read More...
circa 1989
1991
1993
Read More...
More Rules of God Club
04/02/24 04:03 PM Filed in: Christianity | God Club
The first set of rules are here.
[1] Abraham had no scripture, no systematic theology, and no philosophy that we know of. Furthermore, he didn't need them. John 10:27; Heb 3:15
[2] Acts 22:6-9; John 3:3
- The fourth rule of God club is that God is known by experience.1
- The fifth rule of God club is that only God can give you the experience of Himself.2
[1] Abraham had no scripture, no systematic theology, and no philosophy that we know of. Furthermore, he didn't need them. John 10:27; Heb 3:15
[2] Acts 22:6-9; John 3:3
Theodicy: Another Perspective
[Updated 4/5/2024 to add Addendum]
 This spinning dancer is one of my favorite visual effects. I usually see her spinning clockwise but with a change in view I can see her spinning counterclockwise.1
This spinning dancer is one of my favorite visual effects. I usually see her spinning clockwise but with a change in view I can see her spinning counterclockwise.1
This same change of perspective is possible with the "problem" of evil (and divine hiddenness) which are two arguments employed for the non-existence of [a good] God.
The first step to the change of perspective is to remember that logic does not prove its axioms. It cannot, otherwise one is engaging in circular reasoning. The next step is to recall that logic neither adds to, nor subtracts from, the system described by the axioms. If it isn't "in" the axioms, it doesn't appear as a result; if it is "in" the axioms, it doesn't disappear from the result. Logic is a physical operation, not unlike a meat grinder. Beef in, hamburger out; pork in, ground pork out.
These first two steps should be without controversy. So should the third, but it's less familiar; namely, that nature does not impose on us the axioms that we choose. There are more axioms in "mind" space than there are in "meat" space2,3, and nature does not "tell" us which axioms we should use to describe it.
The switchover may come from the observation that the problem of evil and/or divine hiddenness are problems for some people and not for others. Jesus, for example, affirmed the existence of a good God in Luke 18:19 and denied a problem with hiddenness in his sermon on the mount [Matthew 5:8].
So if evil and hiddenness are problems, then the problem is inherent in the axioms; if they aren't problems, they aren't problems inherent in the axioms.4
Since nature doesn't tell us which axioms to choose, why do we choose the axioms we do? Are these "problems" just a mirror to our souls?
AddendumIt's gratifying to find someone coming to the same conclusion independently. In the coffee shop this morning I read the following and had to update this post.

This same change of perspective is possible with the "problem" of evil (and divine hiddenness) which are two arguments employed for the non-existence of [a good] God.
The first step to the change of perspective is to remember that logic does not prove its axioms. It cannot, otherwise one is engaging in circular reasoning. The next step is to recall that logic neither adds to, nor subtracts from, the system described by the axioms. If it isn't "in" the axioms, it doesn't appear as a result; if it is "in" the axioms, it doesn't disappear from the result. Logic is a physical operation, not unlike a meat grinder. Beef in, hamburger out; pork in, ground pork out.
These first two steps should be without controversy. So should the third, but it's less familiar; namely, that nature does not impose on us the axioms that we choose. There are more axioms in "mind" space than there are in "meat" space2,3, and nature does not "tell" us which axioms we should use to describe it.
The switchover may come from the observation that the problem of evil and/or divine hiddenness are problems for some people and not for others. Jesus, for example, affirmed the existence of a good God in Luke 18:19 and denied a problem with hiddenness in his sermon on the mount [Matthew 5:8].
So if evil and hiddenness are problems, then the problem is inherent in the axioms; if they aren't problems, they aren't problems inherent in the axioms.4
Since nature doesn't tell us which axioms to choose, why do we choose the axioms we do? Are these "problems" just a mirror to our souls?





