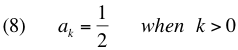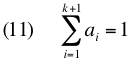Quote
1,2
Whether or not the √2 is irrational cannot be shown by measuring it.
Whether or not the Church-Turing hypothesis is true cannot be shown by thinking about it.
[1] "Euclidean and Non-Euclidean Geometries", Greenberg, Marvin J., Second Edition, pg. 7: "The point is that this irrationality of length could never have been discovered by physical measurements, which always include a small experimental margin of error."
[2] This quote is partially inspired by Scott Aaronson's "PHYS771 Lecture 9: Quantum" where he talks about the necessity of experiments.
Venn Diagrams
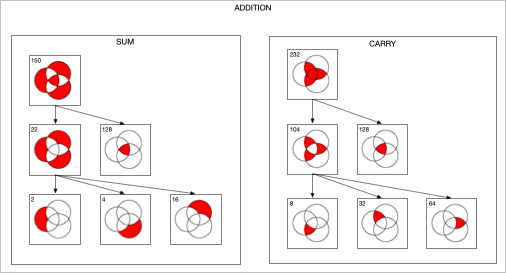
Twelve years ago I played around with designing digital circuits (1, 2, 3) and wrote some code to help in that endeavor. If you can evaluate logical expressions you ought to be able to visualize those expressions. So I extended this code to generate a Venn diagram of an expression. The sum and carry portions of an adder are striking. Click for larger images.
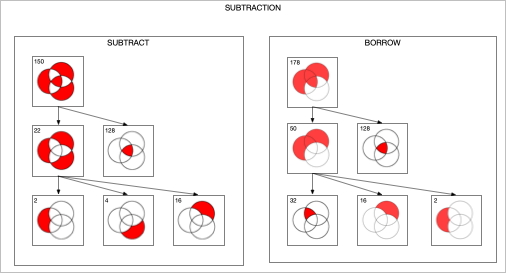
The Venn diagram for the subtraction and borrow equations of a subtraction circuit are similar:
I then produced an animated GIF of all of the 256 Venn diagrams for an equation of 3 variables. The right side is the complement of the equation on the left. 128 images were created, then I used Flying Meat's Retrobatch to resize each image, add the image number, and convert to .GIF format. Then I used the open source gifsicle to produce the final animated .GIF.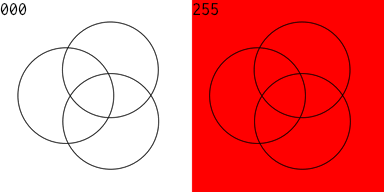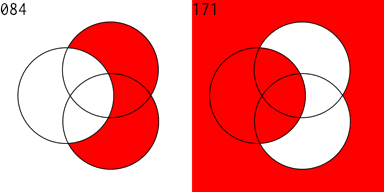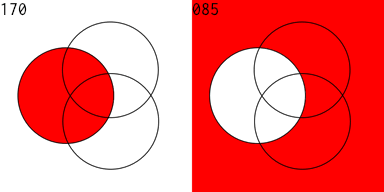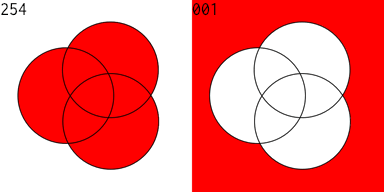
Round to Nearest
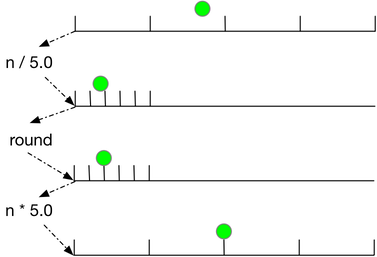
Scale the number line from 0, 5, 10, ... to 0, 1, 2, ...
Round.
Then scale from 0, 1, 2... back to 0, 5, 10...
Extension to values other than 5 is straightforward.
The Lisp code:
(defun round-to (n m)
(if (or (null m) (zerop m))
n
(* (round (/ n (float m))) (float m))))
When Wright Is Wrong
In mathematics, a proof is a sequence of steps that follow an agreed upon set of rules that results in an answer. In computer science, this same idea is called an algorithm. Because Wright attempts to use both the technique of proof by contradiction and the technique of self-reference in his proof, let me begin by showing how these techniques are correctly used.
As an example of a proof by contradiction, let's show that √2 is irrational. By definition, a rational number can be written as the ratio of two integers, a and b, where b is not zero. Let's assume the opposite of what we want to prove, that is, that √2 is rational. That means that:
√2 = a / b (by definition)
Furthermore, let a and b be relatively prime (that is, they have no common divisors).
Then the proof proceeds as follows:
2 = a2 / b2 (by squaring both sides)
2b2 = a2 (by multiplying both sides by b2)
Since a2 is of the form 2n, a2 is an even number. This means that a is an even number (since an odd number times itself results in an odd number). Since a is even, let's rename it as 2c. Then:
√2 = 2c / b (by substitution of equals)
2 = 4c2 / b2 (by squaring both sides)
2b2 = 4c2 (by multiplying both sides by b2)
b2 = 2c2 (by dividing both sides by 2)
This means that b2 is even and therefore b is even.
But since a and b are both even, they share the common divisor 2, which contradicts the initial condition that they be relatively prime.
Since the initial assumption leads to a contradiction, the initial assumption is wrong. Therefore, there are no integers a and b such that a / b = √2 and so √2 is irrational. QED.
Compare this elegant legal proof with invalid proofs. There are many ways a proof can go wrong. Suppose I want to show that I can drive from point A to point B. This means that I have to stay on the roads, follow all traffic laws, and I have to arrive at point B. If I have to drive the wrong way on a one-way street, while I might have arrived at point B, I didn't follow the rules, so the proof isn't valid. Or suppose the car runs out of gas. Running out of gas isn't considered a valid step (nor would be getting into an accident). Suppose I enter a traffic circle and can't get out and I drive forever in a loop. Since the proof doesn't end, it isn't a valid proof.
Driving in a circle — getting stuck in a loop — can still be a useful technique in proofs. It can be used to show that something is undecidable.
Consider the statement:
This statement is false.
If "this statement is false" is true, then "this statement is false" is false. But if "this statement is false" is false, then it's true. We're stuck in a loop. We say that we cannot decide the truth or falsity of the statement.
This statement can also be expressed as two statements:
The next statement is true.
The previous statement is false.
Again, we end up with an infinite loop so the truth of these two statements is undecidable.
Finally, for completeness, it may be that we simply do not know whether something is true, false, or undecidable. Goldbach's Conjecture is a famous unsolved problem in math. Perhaps tomorrow someone will figure it out but, today, its status remains unknown.
With this as background, let's consider Wright's approach to his proof.
If mental states are material, then ideas are just arrangements of matter and a particular idea is one arrangement of atoms and another idea is another arrangement of atoms. Without loss of generality, we could use the number 42 as a label to the arrangement of atoms that corresponds to the idea "all glorps are fleems" and the number 6 as the label to the arrangement of atoms that corresponds to the idea "all fleems are blurgs". Whatever a "glorp", "fleem", or "blurg" is, those ideas would also have a particular material state and could be assigned their own numbers. So far so good. The material states that correspond to ideas have been informally mapped to numbers. 42 represents "all glorps are fleems".
But are all gorps fleems? That is, is "all glorps are fleems" a true statement, false statement, undecidable statement, or an unsolved statement, i.e. a statement that is not known to be true, false, or undecidable? If ideas are material states, what distinguishes a "true" material state from a "false" material state?
Wright doesn't say. But we can fix this deficiency. A proof is a statement about a statement. If something is true, then there exists a set of statements, constructed via agreed upon rules, that end with the label "true" (i.e. the computation that these things are the same) or "false" (the computation that these things are not the same). If we can label statements with numbers and have these numbers represent material states, we can likewise label statements about statements. We could, if we wanted, augment the number associated with a statement with the truth value of the statement. And this number would correspond to a particular arrangement of atoms in the universe. So we can number statements, true statements, false statements, etc.
Now, one part of Wright's proof that needs to be stated is that there should be only one mind in the universe. The arrangement of atoms in Wright's head is a small subset of all of the arrangements of atoms in the universe. When Wright thinks "all glorps are fleems," another sentient creature could, at the same time, be thinking "all glorps are not fleems," while yet another creature could be thinking "I want lunch." I would hope that Wright does not think that what happens locally in his head affects the entire universe, although his commentary on his proof may actually suggest he does. In either case, let's update the proof to say that the universe consists solely of the atoms in Wright's brain, a pencil, and the paper on which statements are written. The proof does not suffer if it ends up showing that there is something in his head that does not correspond to an arrangement of atoms.
So what Wright wants to do is to construct a true statement whose arbitrary number does not map to any arrangement of atoms. If he can do that, then there exists something which we acknowledge to be true, but which doesn't depend on atoms for its truth. It really is immaterial.
So let's now consider the heart of Wright's proof. He reasons as follows:
Statement G is “statement R is true.”[1]), or it does not.
And statement R is “There is no number that represents Statement G.”
A paradox arises: Statement G is either false or true. In other words, either it corresponds to the physical conditions of the universe (the entire universe including all human brains within it
If Statement G is false, then it does not correspond to the conditions of the universe, in which case the conditions of the universe are some number other than 07.
But if Statement G is false then statement R is false, and therefore there is a number that represents Statement G, that is, a condition of atoms whose positions on the cosmic chessboard, including those lined up in my brain, which represent Statement G. We have already said this number is 07. Since the universe cannot both be and not be in condition 07, it is impossible that Statement G be false.
But if statement G is true, then the universe corresponds to the condition that obtains when statement R is true. And if Statement R is true then the statement there is no number that represents Statement G is also true. If there is no number that represents Statement G, or my brain thinking Statement G, or even one of any possible arrangements of atoms in the cosmos, then materialism is false, because then something exists aside from what exists in the arrangement of atoms on our cosmic chessboard.
So what's wrong? A couple of things.
First, the assertion "Statement G is either false or true" isn't necessarily true. G could be undecidable or it could be unknown at this time. If you're going to claim something is true, you have to provide the proof (or take it as an axiom). To prove G, one has to prove "statement R is true". But watch what happens when we start substituting equal things:
G=“statement R is true.”
R=“There is no number that represents Statement G.”
Substituting for G gives: R=“There is no number that represents statement R is true.”
Substituting for R gives: “There is no number that represents There is no number that represents statement R is true is true.”
Trying to express R results in an infinite expansion. Using this technique, G is undecideable. Therefore, the claim that "Statement G is either false or true" is false. And the proof fails.
But we can approach the proof another way. Wright has a strange notion of "truth". He seems to think that "true" statements correspond to physical conditions in the universe (which is true) but that false statements do not. But a false statement is just as much an arrangement of atoms as a true statement is an arrangement of atoms. Clearly this is so. "There are four lights" is a true statement and is an arrangement of atoms of ink on paper or photons emitted from a display. "There are five lights" is a false statement but it, too, is an arrangement of atoms.
Assigning arbitrary numbers to statements only serves to confuse the issue, so let's get rid of the numbers. And let's do this by showing that numbers aren't needed. We can certainly arbitrarily assign numbers to statements, as Wright did. But we can also encode the statements as if they were polynomials. Count the numbers in the character set and that will be the base. Map the first character in the alphabet to 0, the second to 1 and, finally, the last character to base - 1. Then treat each statement as if the letters were coefficients of a polynomial and evaluate it via Horner's method. With this method, each statement can be converted to a number and can be converted back to the original statement. Since numbers and statements are equivalent, we can get rid of the numbers and just use the statements directly.
Then the proof becomes:
Statement G is “statement R is true.”
Statement R is “There is no statement that represents Statement G.”
Statement R is then clearly false, so statement G is false, and the proof falls apart.
Two different ways of looking at the proof give the same result that the proof is wrong.
QED.
[1] The arrangement of atoms in his head affects the entire universe? That some people believe this is not unheard of, as the quote from Gene Wolfe at the end of this post shows.
On Packing Data
[updated 16 April 2010]
The number of bits needed to store an integer, a, a > 0, is:
![]()
Using this formula, 13 bits are needed for the value 7333. In binary, 7333 is 1110010100101, which is indeed 13 bits.
The number of bits needed to store two values, a and b, independently would be:![]()
Using the identity:![]()
The number of bits needed to store the product of a and b is: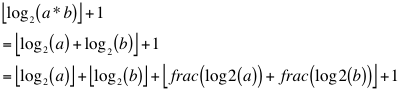
Therefore, we can save one bit by multiplying a and b when![]()
As a trivial example, the values 5 (101) and 6 (110) each require three bits so storing them independently would take 6 bits. However, 6*5 is 30, which takes 5 bits.
Just for curiosity, this graph shows the fractional part of![]()
using the equation![]()
It's an interesting "sawtooth" pattern, with zero values at 2n. The larger version of the graph also shows lines of constant slope between the endpoints of each tooth (in blue), and the point where the tooth equals 0.5 (√2*2n - in red).
Click on the graph for a larger version.
Let's consider a practical application. The start and end of Daylight Savings Time can be specified as "the nth day of the week in month at hour and minute". For example, in 2010, DST in the US begins on the second Sunday in March at 2AM. Let:
d = day of week, Sunday..Saturday = 0..6
r = day rank, first..fifth = 0..4
m = month, January..December = 0..11
h = hour, 0..59
μ = minute, 0..23
Naively, this can be stored in 3+3+4+6+5 = 21 bits.
When multiplying 6 * 5 to save one bit, one of the numbers is needed in order to determine the other. Since we don't a priori know what values were multiplied together, we can't unpack the result. So while the possibility of saving a bit by multiplication made for an interesting analysis, it doesn't help here. There's no point in storing the product of n numbers if you have to know n-1 numbers to recover the nth number.
If we're going to conserve space, it will have to be through application of the first equation. Given two integers, a and b, a requires fewer bits than b when:![]()
So we want to minimize the maximum value of the number being stored.
For the packing algorithm, construct a set, ω, of an upper limit for each item.
Then the largest number that can be encoded is: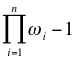
To pack the values vi which correspond to the upper limit values ωi, evaluate:![]()
To unpack rn into values vi which correspond to the upper limit values ωi, evaluate: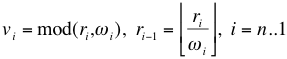
Consider the decimal number 12,345. For base 10 encoding, ωi would be (10, 10, 10, 10, 10), and the largest number that could be encoded would be 99,999. But suppose we knew that the largest possible value of the first digit was one. Then let ωi be (2, 10, 10, 10, 10). The largest value that could be encoded would be 19,999. Since 19,999 < 99,999, it requires fewer bits.
For the daylight savings time values, construct a set, ω, of the maximum value of each item + 1. For (d, r, m, h, μ) this would be (7, 5, 12, 60, 24).
Packing the start times would requlre 20 bits:![]()
Packing both the start and end times would use 39 bits, for a savings of 3 bits.![]()
Thanks to Lee for his comments on this article.
Shiny Things for Suckers
The pitch stated that the coin was plated with 31mg of 24 karat gold.
Let's do the math. 31mg is 0.001093 ounces. Today's gold price is $1096.63/ounce. So the gold in each coin is worth $1.20.
$19.95 + 4.95 shipping and handling = $24.90.
$24.90 for $1.20 worth of gold? Only if you're stupid.
The website is here. If you visit, turn your sound off beforehand since a commercial video starts playing immediately.
What a racket.
More on the Sum of Powers
This is a continuation of this entry which derives the general solution for the coefficients of:
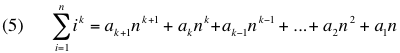
Computed coefficients for 0 <= k <= 10 were provided here.
It was noted that:
![]()
These values were determined by hand. However, it’s easy for LISP code to create the symbolic expression for each coefficient. The prefix expressions used by LISP (e.g. “(+ 3 (* 4 5) 6)” ) were converted to infix form (e.g. “(3 + (4 * 5) + 6)” ) and given to Maxima for simplification. The results are here.
What’s interesting is that the coefficients:
![]()
are all zero.
Now I have to figure out why...
My Contribution to the Mathematical Arts
is

I'm pretty sure we were shown the geometrical derivation of this formula. In college, in late 1975 or early '76, in a Math Lab one problem asked to guess the formula for
In my handwritten lab notebook I used induction to show that the solution to (3) is:
Having solved this specific case, I wanted to see if there was a general solution for any positive integer n and any positive integer exponent. Based on equations (2) and (4), I conjectured that the general solution would be a polynomial of this form:
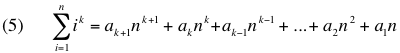
The derivation used induction on the general formula and found that the coefficients to the solution are:
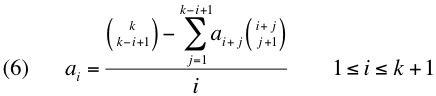
Computed coefficients for 0 <= k <= 10 are here.
Perhaps of interest are these properties of the coefficients: