Quus, Redux
Philip Goff explores Kripke's quss function, defined as:
In English, if the two inputs are both less than 100, the inputs are added, otherwise the result is 5.
(defparameter N 100)
(defun quss (a b)
(if (and (< a N) (< b N))
(+ a b)
5))
Goff then claims:
Rather, it’s indeterminate whether it’s adding orquadding.
This statement rests on some unstated assumptions. The calculator is a finite state machine. For simplicity, suppose the calculator has 10 digits, a function key (labelled "?" for mystery function) and "=" for result. There is a three character screen, so that any three digit numbers can be "quadded". The calculator can then produce 1000x1000 different results. A larger finite state machine can query the calculator for all one million possible inputs then collect and analyze the results. Given the definition of quss, the analyzer can then feed all one million possible inputs to quss, and show that the output of quss matches the output of the calculator.
Goff then tries to extend this result by making N larger than what the calculator can "handle". But this attempt fails, because if the calculator cannot handle bigN, then the conditionals (< a bigN) and (< b bigN) cannot be expressed, so the calculator can't implement quss on bigN. Since the function cannot even be implemented with bigN, it's pointless to ask what it's doing. Questions can only be asked about what the actual implementation is doing; not what an imagined unimplementable implementation is doing.
Goff then tries to apply this to brains and this is where the sleight of hand occurs. The supposed dichotomy between brains and calculators is that brains can know they are adding or quadding with numbers that are too big for the brain to handle. Therefore, brains are not calculators.
The sleight of hand is that our brains can work with the descriptions of the behavior, while most calculators are built with only the behavior. With calculators, and much software, the descriptions are stripped away so that only the behavior remains. But there exists software that works with descriptions to generate behavior. This technique is known as "symbolic computation". Programs such as Maxima, Mathematica, and Maple can know that they are adding or quadding because they can work from the symbolic description of the behavior. Like humans, they deal with short descriptions of large things1. We can't write out all of the digits in the number 10^120. But because we can manipulate short descriptions of big things, we can answer what quss would do if bigN were 10^80. 10^80 is less than 10^120, so quss would return 5. Symbolic computation would give the same answer. But if we tried to do that with the actual numbers, we couldn't. When the thing described doesn't fit, it can't be worked on. Or, if the attempt is made, the old programming adage, Garbage In - Garbage Out, applies to humans and machines alike.
[1] We deal with infinity via short descriptions, e.g. "10 goto 10". We don't actually try to evaluate this, because we know we would get stuck if we did. We tag it "don't evaluate". If we actually need a result with these kinds of objects, we get rid of the infinity by various finite techniques.
[2] This post title refers to a prior brief mention of quss here. In that post, it suggested looking at the wiring of a device to determine what it does. In this post, we look at the behavior of the device across all of its inputs to determine what it does. But we only do that because we don't embed a rich description of each behavior in most devices. If we did, we could simply ask the device what it is doing. Then, just as with people, we'd have to correlate their behavior with their description of their behavior to see if they are acting as advertised.
Truth, Redux
Logic is mechanical operations on distinct objects. At it simplest, logic is the selection of one object from a set of two (see "The road to logic", or "Boolean Logic"). Consider the logic operation "equivalence". If the two input objects are the same, the output is the first symbol in the 0th row ("lefty"). If the two input objects are different, the output is the first symbol in the 3rd row ("righty").
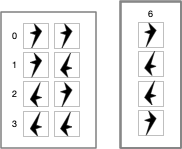
If this were a class in logic, the meaningless symbols "lefty" and "righty" would be replaced by "true" and "false".
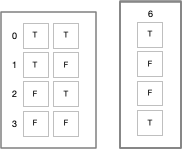
But we can't do this. Yet. We have to show how to go from the meaningless symbols "lefty" and "righty" to the meaningful symbols "T" and "F". The lambda calculus shows us how. The lambda calculus describes a universal computing device using an alphabet of meaningless symbols and a set of symbols that describe behaviors. And this is just what we need, because we live in a universe where atoms do things. "T" and "F" need to be symbols that stand for behaviors.
We look at these symbols, we recognize that they are distinct, and we see how to combine them in ways that make sense to our intuitions. But we don't know we do it. And that's because we're "outside" these systems of symbols looking in.
Put yourself inside the system and ask, "what behaviors are needed to produce these results?" For this particular logic operation, the behavior is "if the other symbol is me, output T, otherwise output F". So you need a behavior where a symbol can positively recognize itself and negatively recognize the other symbol. Note that the behavior of T is symmetric with F. "T positively recognizes T and negatively recognizes F. F positively recognizes F and negatively recognizes T." You could swap T and F in the output column if desired. But once this arbitrary choice is made, it fixes the behavior of the other 15 logic combinations.
In addition, the lambda calculus defines true and false as behaviors.1 It just does it at a higher level of abstraction which obscures the lower level.
In any case, nature gives us this behavior of recognition with electric charge. And with this ability to distinguish between two distinct things, we can construct systems that can reason.
[1] Electric Charge, Truth, and Self-Awareness. This was an earlier attempt to say what this post says. YMMV.
On Rasmussen's "Against non-reductive physicalism"
It should be without controversy that there are more non-physical things than physical things. By some estimates there are 10^80 atoms in the universe. There are an unlimited number of numbers. We can't measure all of those numbers, since we can't put them in one-to-one correspondence with the "stuff" of the universe.
The first thing to note is that if the number of things argues against the physicality of mental states, then mental properties aren't needed, because there are more atoms in the universe than there are in the brain. If the sheer number of things argues against physical mental states then this would be sufficient to prove the claim. But as anyone who plays the piano knows, 88 keys can produce a conceptually infinite amount of music. And one need not postulate non-physicality to do so. Just hook a piano up to random number sources that vary the notes, tempo, and volume. The resulting music may not be melodious, but it will be unique.
Rasmussen presents a "construction principle" which states "for any properties, the xs, there is a mental property of thinking that the xs are physical." Here the confusion between mental property and mental state happens. The argument sneaks in the desired conclusion. After all, if this principle were true, then the counting argument wouldn't be needed. Clearly, there is a mental state when I think "my HomePod is playing Cat Stevens". But whether that mental state is physical or immaterial is what has to be shown. By saying it's a mental property then the assertion is mental states are non-physical and the rest of the proof isn't necessary. It's just proof by assertion.
Rasmussen then gives what he calls "a principle of uniformity" which says, "The divide between any two mental properties is narrower than the divide between physicality and non-physicality." To demonstrate this difference between physical and non-physical, he gives the example of a tower of Lego blocks. His claim is that as Lego block is stacked on Lego block, that both the Lego tower, and the shape of the Lego tower, remains physical. He asserts, "if (say) being a stack of n Lego blocks is a physical property, then clearly so is being a stack of n+1 Lego blocks, for any n." This is clearly false. A Lego tower of 10^90 pieces is non-physical. There aren't enough physical particles in the universe for constructing such a tower. Does the shape of the Lego tower remain physical? This is a more interesting question. A shape is a description of an arrangement of stuff. The shape of an imaginary rectangle and the shape of a physical rectangle are the same. Are descriptions physical or non-physical? To assert one or the other is to beg the question of the nature of mental states.
So we have a counting argument that isn't needed, a construction principle that begs the question, and a principle of uniformity that doesn't match experience.
Having failed to show that mental states are non-physical, in section 3 Rasmussen tries to show that mental states aren't grounded in physicality. The bulk of the proof is in his step B2: "if no member of MPROPERTIES entails any other, then some mental properties lack a physical grounding." He turns the counting argument around to claim that there is a problem of too few physical grounds for mental states. This claim is easily dismissed. First, consider words. The estimated vocabulary of an average adult speaker of English is 35,000 words. There is plenty of storage in the human brain for this. But if we don't know a word, we go to the dictionary to get a new definition and place that definition in short term reusable storage. If we use it enough so that it goes into long term storage, we may forget something to make room for it.
In the case of "infinite" things, we think of them in terms of a short fixed description of behavior, so we don't need a lot of storage for infinite things. The computer statement
is a short description of an endless process. We don't actually think of the entire infinite thing, but rather finite descriptions of the behavior behind the process. [1]
10 goto 10
Rasmussen's proof fails because the claim that there needs to be a unique physical property for each mental state doesn't stand. Much of our physical memory is reusable and we have access to external storage (books, videos, other people). In fact, as I wrote in 2015, "man is the animal that uses external storage". [2]
Since the final sections 4 and 5 aren't supported by 1, 2, and 3, they will be skipped over.
[1] See "Lazy Evaluation" for some ways to deal with infinite sequences with limited storage.
[2] "Man is the Animal...". Almost seven years later, this statement is still unique to me. Don't know why. It's obvious "to the most casual observer."

