The conjecture is that the sum of the numbers from 1 to n, each raised to some power k is a polynomial of the form:



If this is so, then increasing n by 1 is equivalent to:





Substituting the right side of equation 5 into the left side of equation 5a:



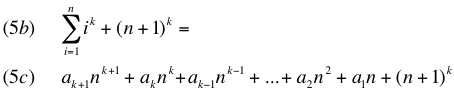
Expanding the last term of 5c with the Binomial Theorem gives:



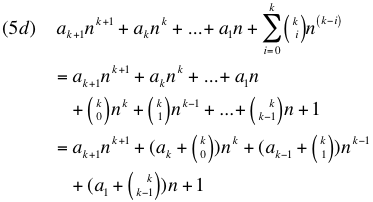
Now we expand the right side of 5a, also using the Binomial Theorem:



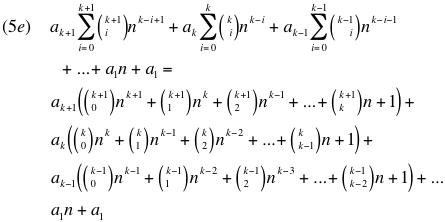
Collecting the coefficients of 5e in table form for easy reference:



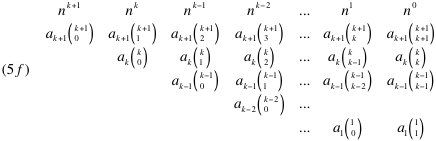
For two polynomials of equal order to be equal, the coefficients must be equal. Therefore, the coefficients of 5d must equal the coefficients of 5f. Aligning the coefficients:



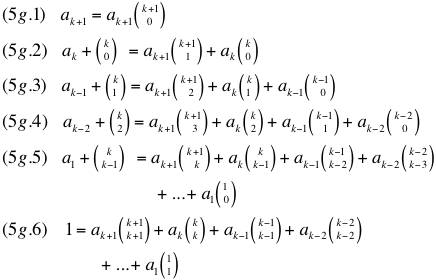
Since k things taken 0 at a time is 1, the last coefficient to the right of the equals sign of 5g.1 through 5g.5 is equal to the first coefficient to the left of the equals sign. so it can be subtracted out. k things taken k at a time is also 1, and k things taken 1 at a time is k, 5g.1 through 5g.6 can be re-written as:



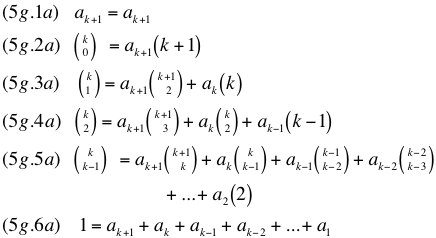
5g.1a adds no useful information, but 5g.2a shows that



Observation of the general pattern for 5g.2a through 5g.6a leads to the solution, equation 6.